 |
Тема № 2 Элементы векторной алгебры и аналитической геометрии
|
|
|
|
2.2. Элементы векторной алгебры и аналитической геометрии в пространстве
Векторные величины (векторы) – это такие величины, которые характеризуются не только своими числовыми значениями, но и направлением.
Для изображения векторных величин служат геометрические векторы. Геометрический вектор – это направленный отрезок.
Координатами вектора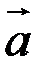 
в прямоугольной системе координат 
называются проекции 
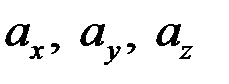вектора 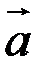на оси координат. Запись 
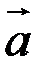означает, что вектор имеет координаты .
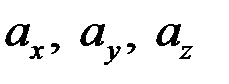Модуль вектора (его длина) вычисляется по формуле
.
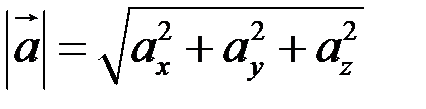Чтобы найти координаты вектора, заданного координатами точек его начала и конца надо найти разности соответствующих координат его конца и начала, т.е. если задан вектор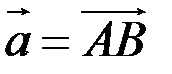 
, где 
, то
.
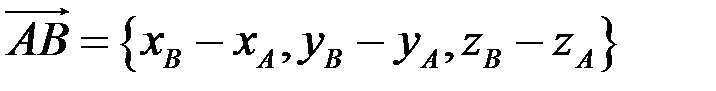Тогда модуль вектора 
находится по формуле
.
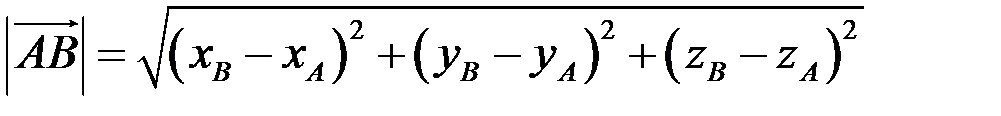Скалярным произведением двух векторов называется число, равное произведению их модулей на косинус угла между ними.
Обозначают: (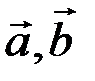
) или 
. По определению
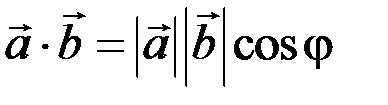, где 
.
Пусть векторы заданы аналитически:
.
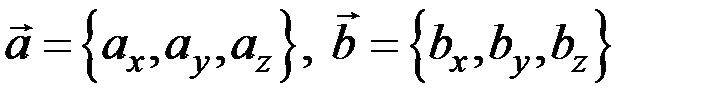Выражение скалярного произведения через координаты перемноженных векторов:
.
Косинус угла между двумя векторами можно найти по формуле
.
Векторным произведением вектора 
на вектор 
называется вектор, обозначаемый символом 
или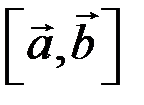 
, определяемый условиями:
1) модуль этого вектора равен произведению модулей перемножаемых векторов на синус угла между ними, т.е.
;
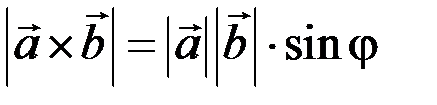2) этот вектор перпендикулярен каждому из перемножаемых векторов, т.е. плоскости, определяемой этими векторами;
3) направлен по перпендикуляру к этой плоскости так, что векторы 
и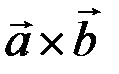 
составляют правую тройку (т.е. если при наблюдении с конца вектора 
кратчайший поворот от вектора 
к вектору 
происходит против часовой стрелки.)
|
|
|
Модуль векторного произведения численно равен площади параллелограмма, построенного на векторах сомножителях – в этом состоит геометрический смысл модуля векторного произведения:
.
Пусть даны два вектора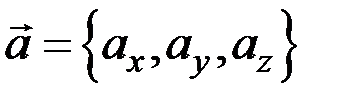 
и 
. Выражение векторного произведения через координаты перемножаемых векторов:
.
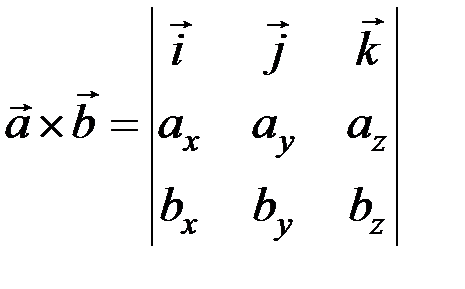Смешанным произведением трех векторов 
называется число, равное скалярному произведению вектора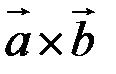 
на вектор 
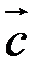, т.е. 
.
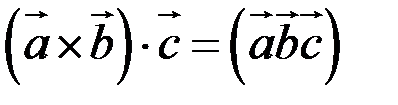Если векторы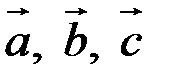 
заданы своими прямоугольными координатами 
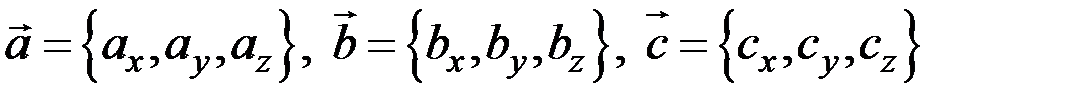, то их смешанное произведение вычисляется по формуле
.
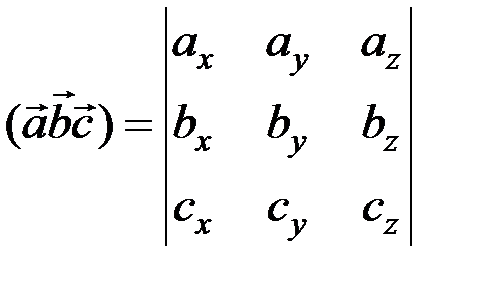Геометрический смысл смешанного произведения: объем параллелепипеда, построенного на 3-х некомпланарных векторах, равен абсолютной величине их смешанного произведения
.
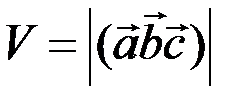Тогда объем треугольной пирамиды, построенной на этих же векторах, находится по формуле
.
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Если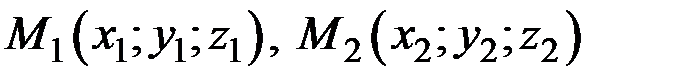 
, 
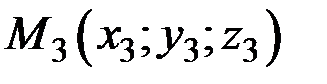три данные точки, не лежащие на одной прямой, а 
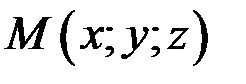произвольная точка плоскости, то уравнение плоскости, проходящей через три точки, имеет вид
.
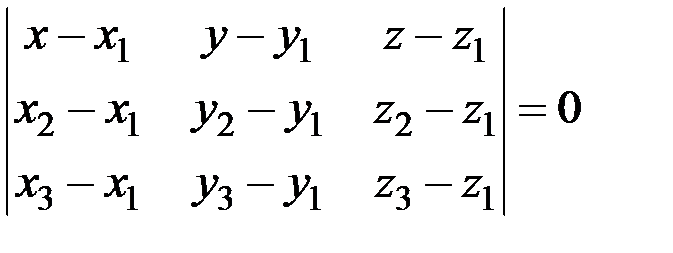Уравнение прямой, проходящей через две точки пространства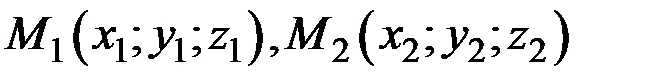 
имеет вид
.
Угол между прямой и плоскостью находится по формуле
,
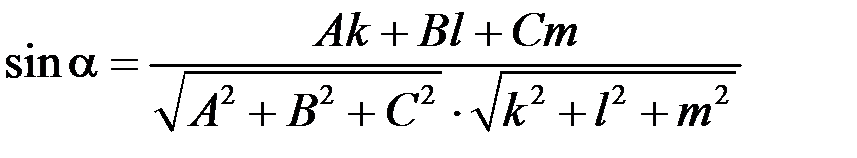где коэффициенты выбирают из канонических уравнений прямой
и общего уравнения плоскости
,
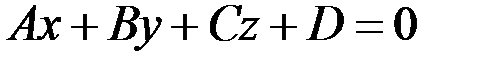где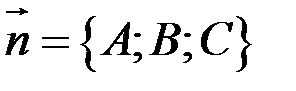 
- вектор нормали к плоскости.
Условие перпендикулярности прямой и плоскости:
.
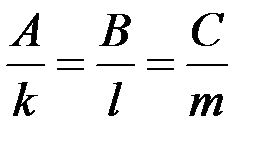Пример
Даны вершины треугольной пирамиды 
Найти:
1) угол между ребрам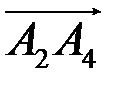и 
и 
;
2) площадь грани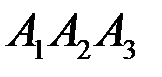 
;
3) объем пирамиды 
;
4) длину высоты, опущенной из вершины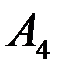 
на грань 
;
5) уравнение высоты, опущенной из вершины 
на грань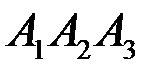 
.
Решение
| А 4 А 2 В А 1 А 3 Рис. 2 | 1) Угол между ребрам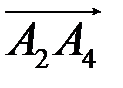и  и 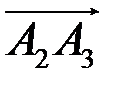 находим с помощью скалярного произведения векторов по формуле
 ,
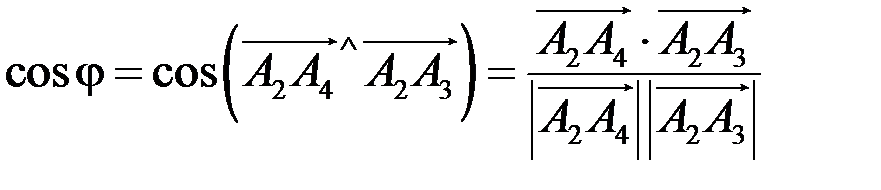найдем координаты векторов
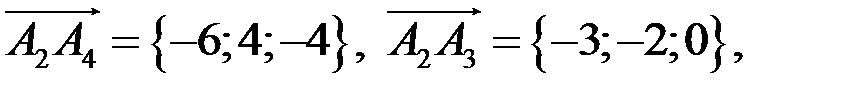тогда косинус угла между векторами
 .
|
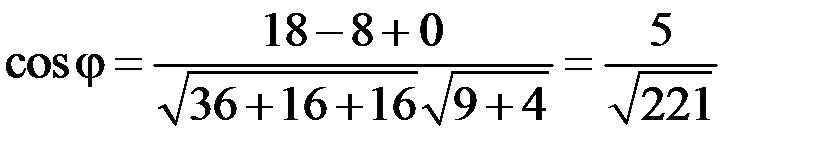2) Площадь грани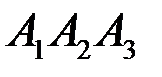 
находим с помощью векторного произведения векторов. Найдем координаты вектора 
, тогда площадь треугольника находим по формуле
|
|
|
.
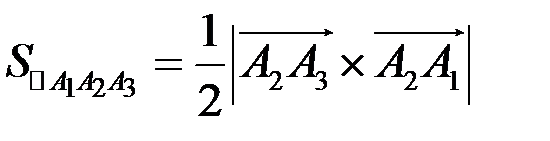Найдем векторное произведение векторов
модуль векторного произведения равен
,
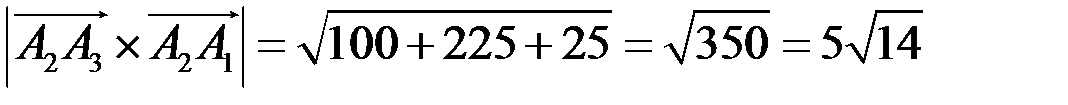откуда находим площадь треугольника
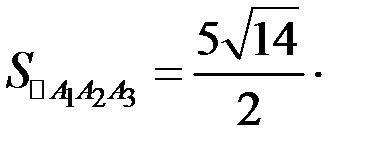
3) Объем пирамиды находим с помощью смешанного произведения векторов по формуле
,
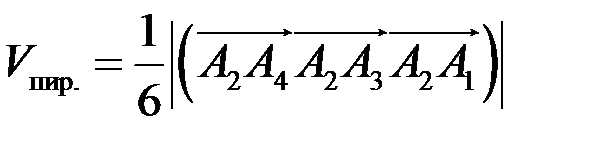так как выше найдены координаты векторов
,
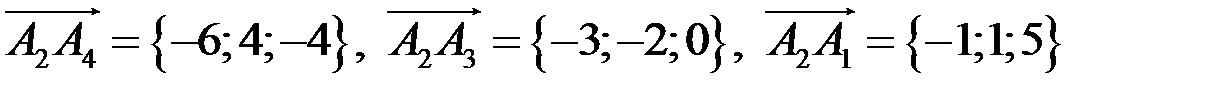подставим координаты векторов в формулу, получим
.
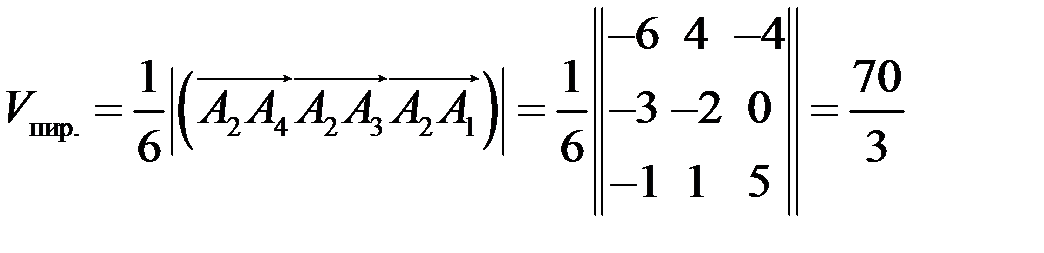4) Для нахождения длины высоты h, опущенной из вершины 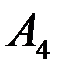на грань применим формулу
,
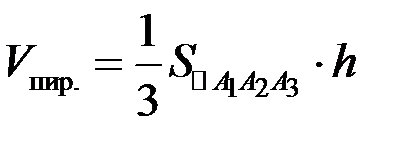откуда находим
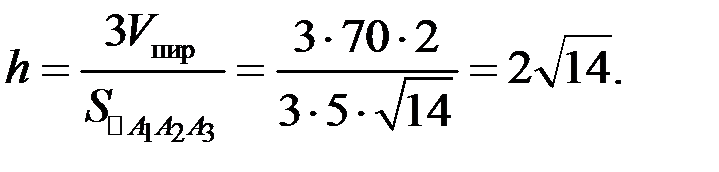
5) Общее уравнение плоскости 
:
,
нормальный вектор плоскости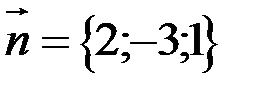 
.
Уравнение высоты 
: 
.
Условие перпендикулярности прямой и плоскости: 
.
В нашем случае 
, тогда уравнение высоты имеет вид
|
|
|
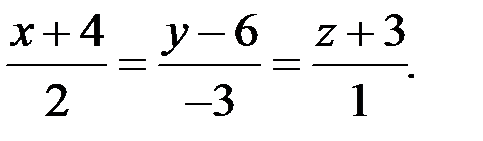
