 |
Решение систем линейных алгебраических уравнений
|
|
|
|
(СЛАУр)
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
 . (1)
. (1)
Если хотя бы одно из чисел 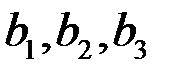 не равно нулю, то такая система называется неоднородной. Если же
не равно нулю, то такая система называется неоднородной. Если же 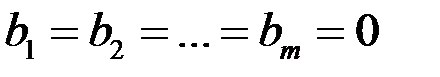 , то такая система называется однородной.
, то такая система называется однородной.
Решением системы (1) называется упорядоченная совокупность чисел 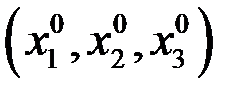 , которая при подстановке в систему обращает все уравнения системы в верные равенства.
, которая при подстановке в систему обращает все уравнения системы в верные равенства.
Если система имеет решение, то она называется совместной, если не имеет решения – то несовместной. Если система имеет единственное решение, то она называется определенной, если более одного решения, то – неопределенной.
Формулы Крамера для решения СЛАУр
Если определитель системы  , то эта система имеет единственное решение, которое можно получить по формулам Крамера. Формулы Крамера имеют вид
, то эта система имеет единственное решение, которое можно получить по формулам Крамера. Формулы Крамера имеют вид
 ,
,
где
 .
.
В знаменателях этих формул стоит определитель системы  , а в числителях – определители, которые получаются из определителя системы
, а в числителях – определители, которые получаются из определителя системы  заменой коэффициентов при соответствующих неизвестных столбцом свободных членов.
заменой коэффициентов при соответствующих неизвестных столбцом свободных членов.
Пример 1.
Решить систему  по формулам Крамера.
по формулам Крамера.
Решение
Формулы Крамера:  . Вычислим определители:
. Вычислим определители:
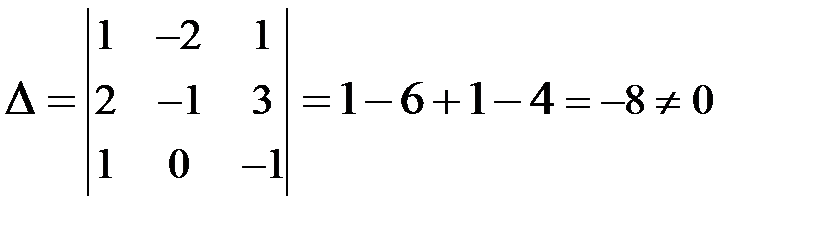 ,
,
 , тогда
, тогда
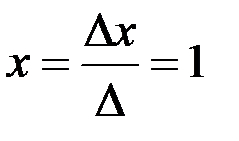 ,
,  ,
, 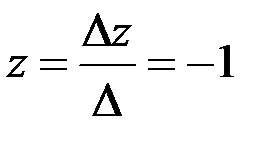 .
.
Итак,  ,
, 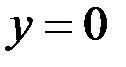 ,
, 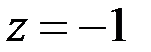 .
.
Ранг матрицы
Пусть дана матрица  .
.
Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров. Обозначение: rang A, r (А) или r.
Очевидно,  – меньшее из чисел m и n.
– меньшее из чисел m и n.
Минор, порядок которого определяет ранг матрицы, называется базисным. Вычисление всех миноров отличных от нуля трудоемкая операция. На практике для вычисления r (A) используют метод Гаусса.
Элементарными преобразованиями называются следующие действия над матрицами:
1. Вычеркивание нулевой строки.
|
|
|
2. Умножение какой либо строки на число.
3. Прибавление к одной из строк другой строки, умноженной на любое число.
4. Перестановка двух столбцов или двух строк.
Теорема 1. Ранг матрицы не меняется при элементарных преобразованиях.
Рассмотрим матрицу специального вида
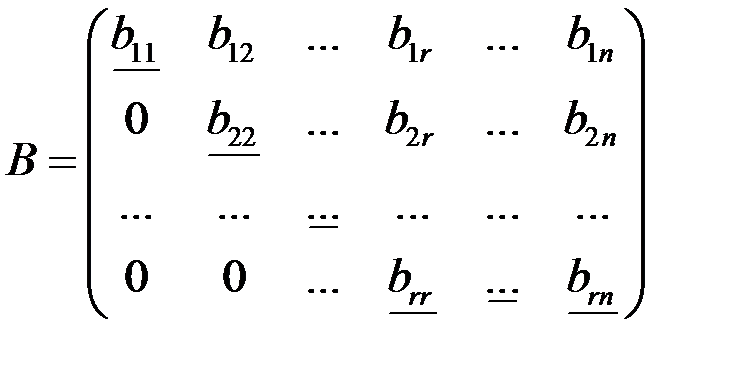
в которой все «диагональные элементы» 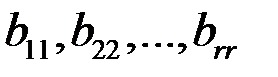 отличны от нуля, а все элементы расположенные ниже диагональных, равны нулю. Такую матрицу будем называть трапециевидной. При r = n она будет треугольной.
отличны от нуля, а все элементы расположенные ниже диагональных, равны нулю. Такую матрицу будем называть трапециевидной. При r = n она будет треугольной.
Теорема 2. Ранг трапециевидной матрицы равен числу ее ненулевых строк.
Теорема 3. Всякую матрицу можно с помощью конечного числа элементарных преобразований привести к трапециевидному виду.
Метод Гаусса вычисления ранга матрицы состоит в приведении матрицы к трапециевидному виду и в подсчете ее ненулевых строк.
Пример 2.
Найти ранг матрицы 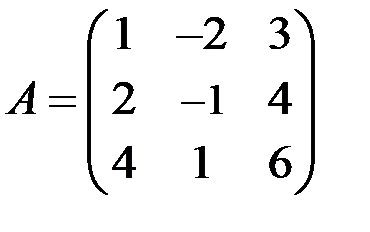 .
.
Решение
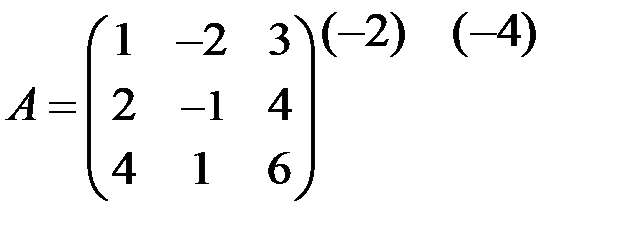 ~
~ 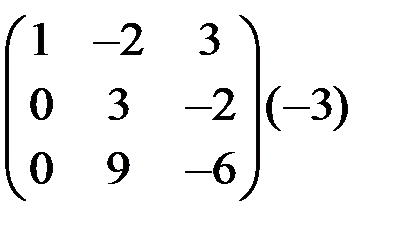 ~
~ 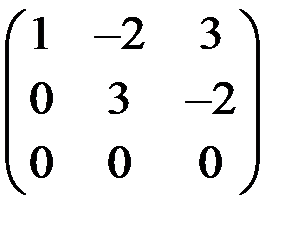
На первом шаге первую строку матрицы умножили на (-2) и сложили со второй строкой, умножили первую строку на (-4) и сложили с третьей строкой. На втором шаге вторую строку умножили на (-3) и сложили с третьей строкой. Нулевую строку вычеркнули. Таким образом, ранг матрицы r = 2.
Метод Гаусса решения СЛАУр
Пусть дана система линейных алгебраических уравнений (СЛАУр)
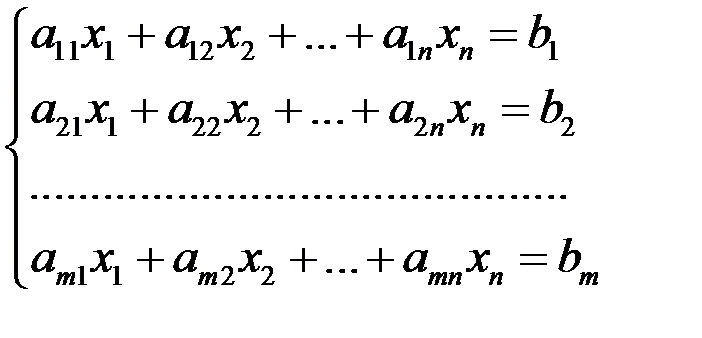
Поставим задачу: исследовать данную систему, т.е. выяснить, не решая ее, совместна она или несовместна, а если совместна, то определенна она или неопределенна.
На все эти вопросы отвечает теорема Кронекера - Капелли.
Пусть дана матрица системы 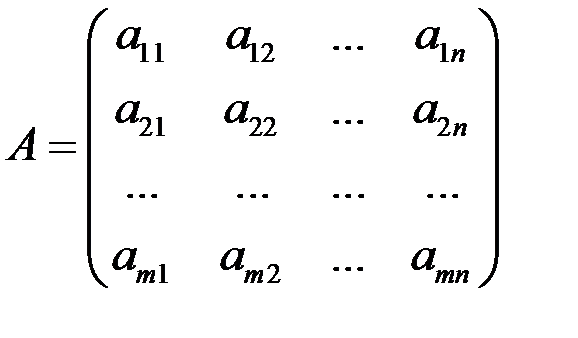 .
.
Рассмотрим расширенную матрицу системы
 .
.
Теорема Кронекера – Капелли.
СЛАУр совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицы системы:
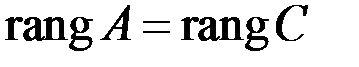 или
или 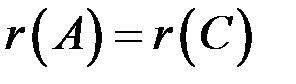 .
.
Замечание
Если 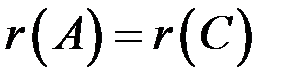 и
и  , где n – число неизвестных, то система определенна; если
, где n – число неизвестных, то система определенна; если  , то система неопределенна, если же
, то система неопределенна, если же  , то система несовместна.
, то система несовместна.
Метод Гаусса решения СЛАУр состоит в следующем.
|
|
|
1. Выписывают расширенную матрицу системы
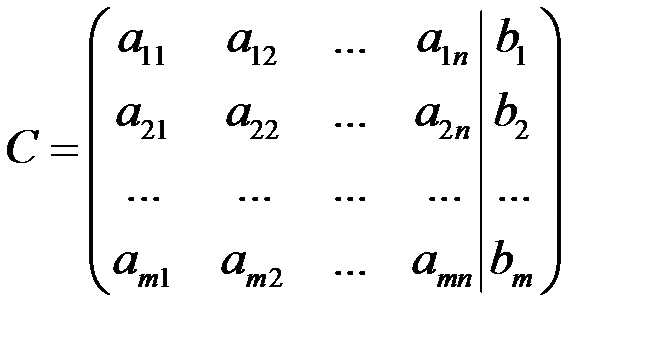
и с помощью элементарных преобразований приводят ее к трапециевидному виду.
2. Применяя теорему Кронекера – Капелли, исследуют систему, получая один из случаев:
– система совместна и определенна,
– система совместна и неопределенна,
– система несовместна.
Трапециевидная форма расширенной матрицы С в каждом из этих случаев имеет вид:
1) С ~ 
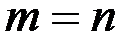 ,
,  ,
,
следовательно, система определенна, имеет единственное решение,
2) С ~ 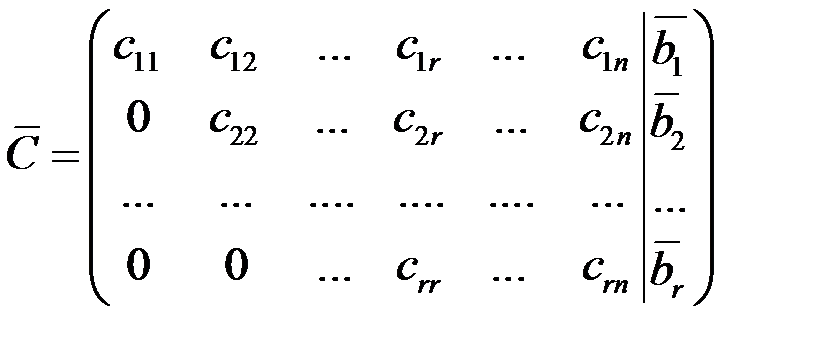
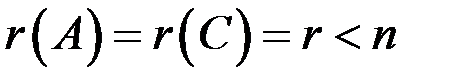 ,
,
следовательно, система неопределенна, имеет бесконечное множество решений,
3) если какая-либо строка матрицы С имеет вид  , то система несовместна (решений нет).
, то система несовместна (решений нет).
3. Для решения системы, если оно существует, следует записать новую систему, отвечающую полученной трапециевидной матрице, которая является более простой по сравнению с исходной и решить ее (обратный ход).
Пример 3.
Исследовать и решить СЛАУр:  .
.
Решение
Составим расширенную матрицу и проведем над ней эквивалентные преобразования для определения 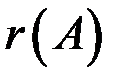 и
и  .
.
 ~
~  ~
~
 ~
~ 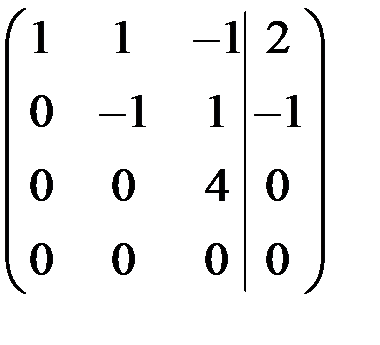 ,
,
Таким образом,  , следовательно, по теореме Кронекера – Капелли система совместна и определенна.
, следовательно, по теореме Кронекера – Капелли система совместна и определенна.
Составим систему, соответствующую последней матрице, эквивалентную исходной:
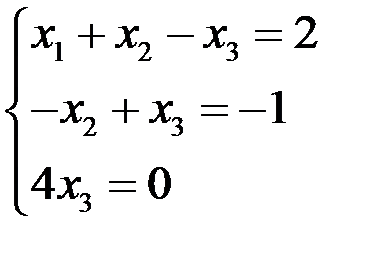 Þ
Þ 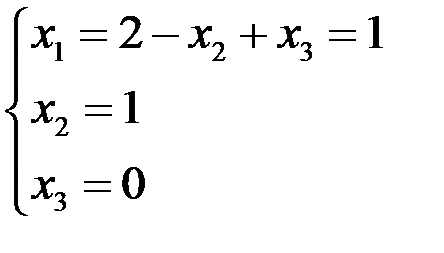 .
.
Таким образом, 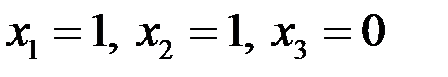 .
.
Пример 4.
Исследовать и решить СЛАУр: 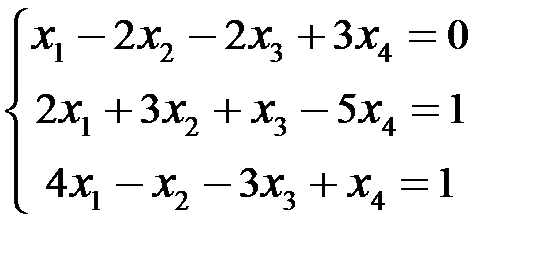 .
.
Решение
 ~
~ 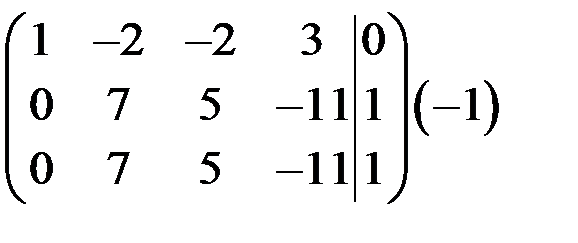 ~
~ 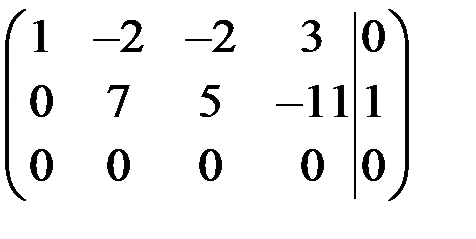
Так как  , следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
, следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
Последней матрице соответствует система:
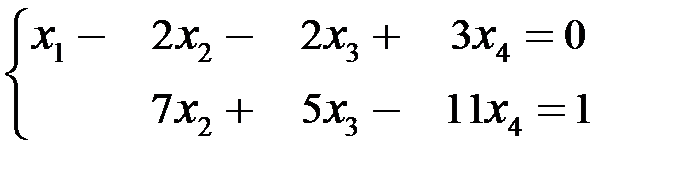 Þ
Þ 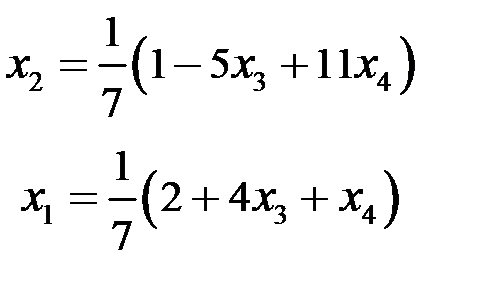
где  и
и 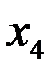 – произвольные параметры.
– произвольные параметры.
Пример 5.
Исследовать и решить СЛАУр: 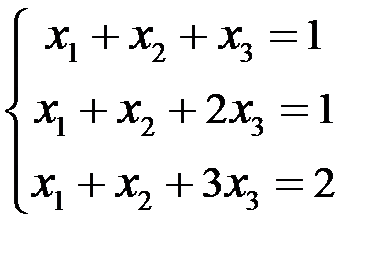
Решение
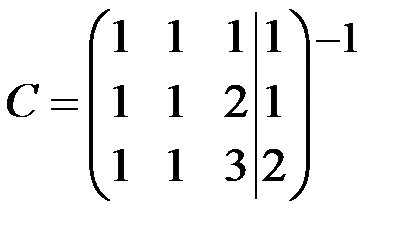 ~
~ 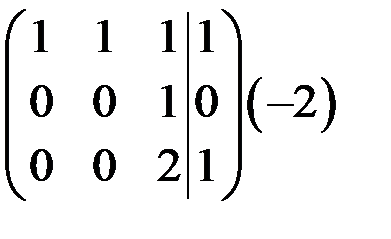 ~
~ 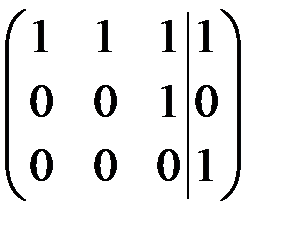
Так как 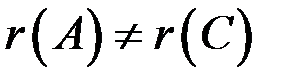 , то система несовместна (решений нет).
, то система несовместна (решений нет).
Пример 6.
Исследовать и решить СЛАУр: 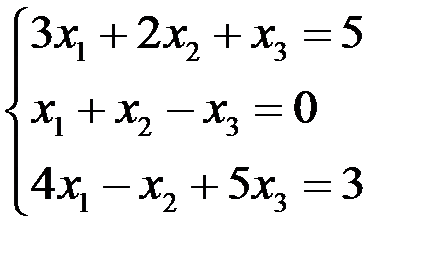 .
.
Решение
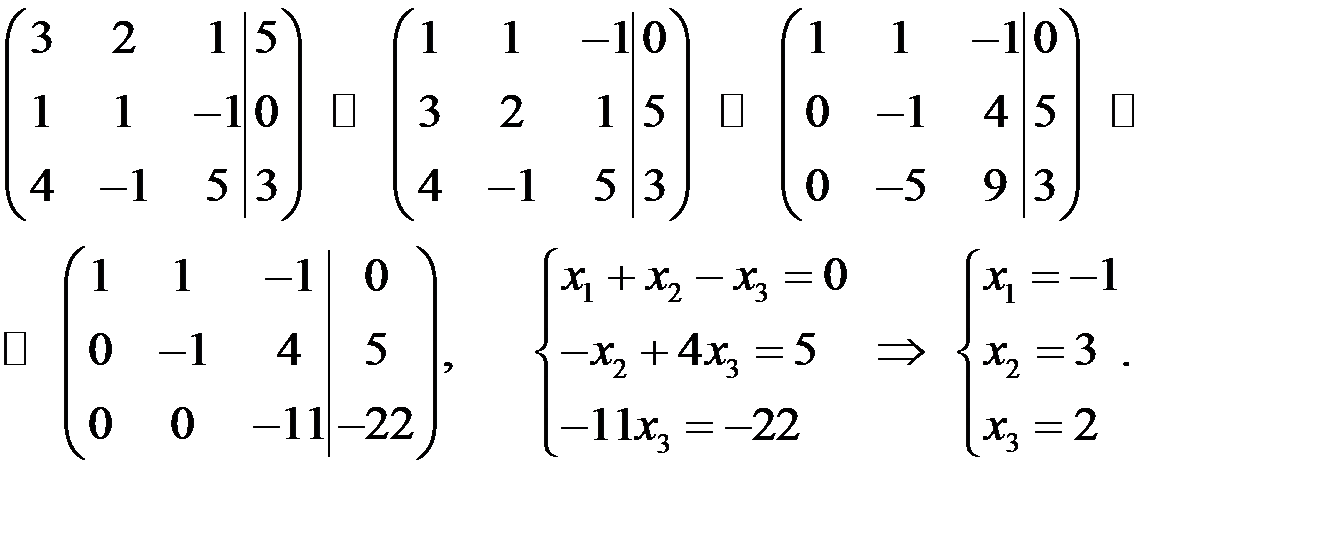
Таким образом,  .
.
|
|
|


