 |
Раздел 2. Основы теории вероятностей
|
|
|
|
Тема 2.1. Случайные события. Понятие вероятности события.
Задание 3. Вычисление вероятности событий по классической формуле определения вероятностей.- 2ч.
Задание для самостоятельной внеаудиторной работы:
1.Выучите классическое определение вероятности события. Изучите свойства вероятности события. Повторите схему решения комбинаторных задач.
2. Подбрасываются два игральных кубика. Какова вероятность, что:
- сумма очков равна 8;произведение очков равно 8;
- сумма очков больше 12;произведение очков меньше 36.
3. Пять мячей, пронумерованных от 1 до 5, положены в ящик; после чего они вынимаются один за другим случайным образом. Какова вероятность того, что их будут вынимать в следующем порядке: 5, 2, 4, 3, 1?
4. В отделе работают 6 мужчин и 4 женщины. По табельным номерам отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины.
5. Бросаются одна за другой две игральные кости. Чему равна: а) вероятность не выпадения дубля; б) вероятность того, что число очков на одной кости в два раза больше числа очков на другой кости; в) сумма выпавших очков равна 8, а разность 4?
6. Числа от 1 до 15 написаны на 15 мячах (по одному на каждом мяче). Выбирается наугад один мяч. Чему равна вероятность того, что число, написанное на этом мяче: а) делится на 5; б) четное; в) нечетное; г) является точным квадратом; д) является двузначным; е) является простым; ж) является простым и таково, что число, меньшее его на 2, также простое?
Методические указания по выполнению работы:
Классической вероятностью появления события А называется отношение количества благоприятных событию А исходов испытаний к общему количеству всех возможных исходов эксперимента.
|
|
|
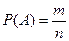, где 
- количество благоприятных исходов; 
- общее количество исходов эксперимента. Эта формула носит название классического определения вероятности.
Пример 1. Бросают игральный кубик, на гранях которого от 1 до 6 точек. Найти вероятность того, что
выпадет число, не больше 3; выпадет четное число; выпадет 7; выпадет число, большее 4.
Решение:
а) В данном случае, как и в примере 1, общее количество исходов 6, однако благоприятным событиями будет выпадение чисел 1, 2, 3. Следовательно, искомая вероятность в данном случае будет равна
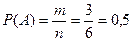
б) Количество четных цифр на гранях кубика три. Это числа 2, 4, 6. Искомая вероятность по формуле (1):
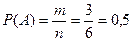
в) На гранях кубка самое большое число 6, следовательно, количество благоприятных событий равно 0.
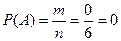
т.е. выпадение числа 7 является невозможным событием.
г) Таких чисел только два, это 5 и 6, следовательно
Сравнивая результаты вариантов а) и б), можно сказать что событие "выпадение числа не большего числа 3" и "выпадение четной цифры" равновероятны, а событие "выпадение четной цифры" более вероятно чем "выпадение цифры большей, чем 4".
Пример 2.
В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Используя классическое определение теории вероятности определить, какова вероятность того, что обе детали окажутся бракованными.
Решение:
Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 23 деталей вынуть две, т.е. числу сочетаний из 23 элементов по 2:
Число благоприятных исходов
Следовательно, искомая вероятность
алгебра событий»Список литературы:
1.Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учредж. СПО / М.С. Спирина, П.А. Спирин. - М: Изд. центр «Академия», 2012.-Глава 1, п.1.7., стр.48.
2.Калинина В.Н., Панкин В.Ф.Математическая статистика: учебник для ССУЗов / В.Н. Калинина, В.Ф.Панкин -М: Высш.шк., 2001.–Глава 2, §2.3, стр. 28.
|
|
|
Раздел 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
|
|
|
