 |
Задание 16. Сбор и обработка статистических данных. – 4 ч.
|
|
|
|
Задание для самостоятельной внеаудиторной работы:
1.Повторите структуру выборочного метода. Проанализируйте дискретный и интервальный вариационный ряд, их геометрическую иллюстрацию? Укажите формулы для вычисления числовых характеристик?
2.С целью изучения динамики спроса на компьютеры фирма ежедневно подсчитала число проданных компьютеров в течение месяца: 3, 5, 4, 7, 0, 1, 3, 5, 5, 2, 3, 4, 3, 6, 6, 2, 0, 5, 3, 5, 6, 4, 4, 3, 1, 4, 2, 2, 4, 5. Составьте статистическое распределение выборки, постройте полигон частот, найдите числовые характеристики выборки.
3. Администрацию магазина интересует частота покупок калькуляторов. Менеджер в течении января регистрировал данные о покупке МК и собрал следующие данные: 8, 4, 4, 9, 3, 3, 1, 2, 0, 4, 2, 3, 5, 7, 10, 6, 5, 7, 3, 2, 9, 8, 1, 4, 6, 5, 4, 2, 1, 0, 8.
Составьте вариационный ряд оценок и найдите числовые характеристики выборки. Постройте полигон частот.
4. По данным выборочного обследования получено следующее распределение по среднедушевому доходу
| Среднедушевой доход семьи в месяц, у.е. | до | 25 – 50 | 50 – 75 | 75 – 100 | 100 – 125 | 125 – 150 | 150 и выше |
| Количество обследованных семей |
Найдите выборочную среднюю и выборочное среднеквадратичное отклонение среднедушевого дохода семьи. Постройте гистограмму.
5.Проведите собственное статистическое исследование. Обработайте и оформите статистические данные исследования.
Методические указания по выполнению работы:
Совокупность предметов или явлений, объединённых каким – либо общим признаком или свойством качественного или количественного характера, называется объектом наблюдения.
- Количественным называется признак, значения которого выражаются числами.
|
|
|
- Качественным называется признак, характеризующийся некоторым свойством или состоянием элементов совокупности.
Статистические данные – это сведения о том, какие значения принял интересующий исследователя признак в статистической совокупности.
Статистическая совокупность называется генеральной совокупностью, если исследованию подлежат все элементы совокупности.
Выборочной совокупностью, или просто выборкой, называют часть элементов генеральной совокупности подлежащих исследованию. Она извлекается из генеральной совокупности случайно, чтобы каждый объект имел равные шансы быть отобранным.
Значения признака, которые при переходе от одного элемента совокупности к другому изменяются, называются вариантами и обозначаются маленькими латинскими буквами. Порядковый номер варианта называется рангом.
Ряд значений признака, расположенный в порядке возрастания или убывания с соответствующими им весами, называется вариационным рядом.
В качестве весов выступают частоты или частости.
Частота (mi) показывает, сколько раз встречается тот или иной вариант в статистической совокупности.
Частость или относительная частота (wi) показывает, какая часть единиц совокупности имеет тот или иной вариант к сумме всех частот ряда. Частость рассчитывается как отношение частоты того или иного варианта к сумме всех частот ряда

Вариационные ряды бывают дискретными и интервальными.
Дискретные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга не менее чем на некоторую конечную величину. В дискретных вариационных рядах задаются точечные значения признака. Общий вид дискретного ряда показан в таблице.
| Значения признака (хi) | х1 | х2 | … | хk |
| Частоты (mi) | m1 | m2 | … | mk |
Интервальные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга на сколь угодно малую величину. Значения признаков в них задаются в виде интервалов. Общий вид интервального ряда имеет вид
|
|
|
| Значения признака (хi) | a1 – a2 | a2 – a3 | … | ai-1 - ai |
| Частоты (mi) | m1 | m2 | … | mi |
В интервальных вариационных рядах в каждом интервале выделяют верхнюю и нижнюю границы.
Разность между верхней и нижней границами интервала называется интервальной разностью или длиной интервала. В общем виде интервальную разность ki представим как
ki= xi (max) - xi (min)
Первый и последний интервалы могут быть открытыми, т.е. иметь только одну границу.
Если интервалы в вариационных рядах имеют одинаковую длину, их называют равновеликими, в противном случае неравновеликими.
При построении интервального ряда (если строится ряд с равными интервалами), для определения оптимальной величины интервалов применяют формулу Стэрджесса
 ,
,
где n число единиц совокупности; xmaxи xmin – наибольшее и наименьшее значения вариационного ряда.
Дискретный вариационный ряд графически можно представить с помощью полигона распределения частот или частостей.

Гистограммой частот выборки называется ступенчатая фигура, состоящая из прямоугольников, построенных на интервалах длиной d, высота которых равна отношению m i/ d (плотность частоты на данном интервале).

 Числовые характеристики вариационного ряда
Числовые характеристики вариационного ряда
Выборочное среднее - 
Выборочная дисперсия -  ,
, 
Выборочное среднеквадратическое отклонение - 
Для интервального вариационного ряда в качестве x i выбирают середину соответствующего интервала.
Пример 1. 3а десять дней работы малое предприятие «Дюймовочка» получало дневную прибыль (в у.е.): 4, 5, 8, 5, 9, 3, 4, 3, 3, 3.
Составьте дискретный и интервальный вариационные ряды оценок и найдите числовые характеристики выборки. Постройте полигон и гистограмму частот.
Решение. Выполним ранжирование данных, т.е. расположим их в порядке возрастания: 3,3,3,3,4,4,5,5,8,9.
Составим дискретный вариационный ряд:
| x i | ∑ | |||||
| m i |
В нашем примере полигон частот выглядит следующим образом:

Составим интервальный вариационный ряд. Зададим ширину интервала d. Пусть она равна 2. Интервальный вариационный ряд будет иметь вид:
|
|
|
| x i | 3-5 | 5-7 | 7-9 | ∑ |
| m i |
Построим гистограмму. Она будет состоять из трех прямоугольников, построенных на интервалах длиной d = 2 с высотами m i/ d:
| высота | гистограмма частот |
| h1 | |
| h2 | |
| h3 |

Найдем числовые характеристики выборки:
Для дискретного вариационного ряда
 =
= 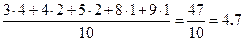 .
.


Тогда  26.3 – (4.7)2 = 4.21.
26.3 – (4.7)2 = 4.21.  .
.
Для интервального вариационного ряда в качестве x i берут середину интервалов.
 =
=  ;
;

 ,
,  29.6 – (5.2)2 = 2.56,
29.6 – (5.2)2 = 2.56,
 .
.
Список литературы:
1.Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учредж. СПО / М.С. Спирина, П.А. Спирин. - М: Изд. центр «Академия», 2012.-Глава 3, п.3.3., стр.194.
2.Калинина В.Н., Панкин В.Ф. Математическая статистика: учебник для ССУЗов / В.Н. Калинина, В.Ф.Панкин - М: Высш.шк., 2001. – Глава 8, §8.1 – 8.6, стр. 132.
|
|
|


