 |
Задание 5. Формула полной вероятности. Формула Байеса – 2 ч.
|
|
|
|
Задание для самостоятельной внеаудиторной работы:
1.Выучите формулу полной вероятности.
2.Изделия были произведены с использованием двух технологических линий. На первой линии было произведено 2 изделия, на второй линии: 3 изделия. Вероятность того, что изделие будет отличного качества при производстве на первой линии равна 0.75, на второй – 0.7. Какова вероятность того, что случайно выбранной изделие будет отличного качества?
3. На складе имеется 28 комплектующих изделий от двух компаний поставщиков, из них 20 изделий от первой компании. Известно, что с вероятностью 0.7 среди поставок первой компании встречаются изделия, выполненные по новейшей технологии. Среди изделий второй компании такие встречаются с вероятностью 0.8. Какова вероятность того, что случайным образом выбранное изделие выполнено по новейшей технологии?
4.На склад поступили электроутюги, 80% с первого завода и 20% со второго. Среди продукции первого завода 90% выдерживают трехлетний гарантийный срок, со второго завода – 95%. Какова вероятность того, что взятый наугад со склада утюг выдержит трехлетний гарантийный срок? Какова вероятность того, что утюг с первого завода?
5.Имеется три партии ламп по 100, 200 и 300 штук. В первой партии 80% ламп с продолжительностью работы более 1 000 часов, во второй - 75%, в третьей – 60%. Какова вероятность, что случайно выбранная лампа, проработавшая более 1000 часов, была взята из второй партии?
6. Студент подготовил 10 билетов из 25. Когда вероятность взять известный билет больше: 1) студент зашел на экзамен первым; 2) студент зашел вторым.
Методические указания по выполнению работы:
1. Запишите случайное событие А, вероятность которого необходимо найти по условию задачи.
|
|
|
2. Сформулируйте гипотезы Н 1, Н 2, …, Нn при которых может наступить событие А и вычислите вероятности их осуществления Р(Н1), Р(Н2)… Р(Н п).
3. Найдите условные вероятности события А при выполнении гипотез Н 1, Н 2, …, Нn: 
, 
… 
4. Если необходимо найти вероятность события А, то примените формулу полной вероятности. Если событие А произошло, и нужно найти вероятность того, что была выполнена какая-либо из гипотез, используйте формулу Байеса.
Пусть событие А может наступить при условии появления одного из несовместных событий Н1, Н2,..., Н n, образующих полную группу.
Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами.
Вероятность появления события А определяется по формуле полной вероятности:
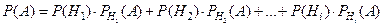
Допустим, что произведено испытание, в результате которого появилось событие А. Выясним, как изменились вероятности гипотез после того, как появилось событие А.
Полученные формулы называют формулами Байеса.
Формулы Байеса позволяют переоценить вероятность гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Пример 1. Для участия в спортивных студенческих соревнованиях, выделено из первой группы – 4, из второй – 6, из третьей – 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадёт в сборную института, равны соответственно 0,9, 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. Какой группе вероятнее всего принадлежит этот студент?
Решение.
Испытание выбор студента из трех групп.
Событие А-выбранный наудачу студент попадет в сборную.
Н 1 –студент из первой группы, Р (Н 1)= 
Н 2 - студент из второй группы, Р (Н 2)= 
Н 3 - студент из третьей группы, Р (Н 3)= 
В задаче необходимо найти вероятность того, что случайно выбранный студент попадет в сборную.
(вероятность того, что выбранный студент попадет в сборную при условии, что он из первой группы);
|
|
|
(вероятность того, что выбранный студент попадет в сборную при условии, что он из второй группы);
(вероятность того, что выбранный студент попадет в сборную при условии, что он из третьей группы);
Вероятность попадания в сборную P (A) вычислим по формуле полной вероятности:
P (A) = (4/15)×0,9 + (6/15)×0,7 + (5/15)×0,8 = 11,8/15 = 59/75.
Найдём вероятность того, что выбранный студент попал в сборную
из первой группы: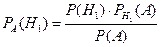 
= (4/15)×0,9/(59/75) = 18/59;
из второй 
= (6/15)×0,7/(59/75) = (4,2/15)×(75/59) = 21/59;
из третьей 
= (5/15)×0,8×(75/59) = 20/59.
|
|
|
