 |
Задание 9. Нахождение числовых характеристик распределения ДСВ – 2 ч.
|
|
|
|
Цель: формирование умения находить функции от ДСВ, вычислять числовые характеристики ДСВ, заданной законом распределения, строить графики функций от ДСВ.
Задание для самостоятельной внеаудиторной работы:
1. В таблице (номер задания совпадает с последней цифрой в номере журнала) дан закон распределения ДСВ Х.
Найдите: 1. неизвестную вероятность; 2. математическое ожидание; 3.дисперсию; 4. среднеквадратическое отклонение; 5. интегральную функцию распределения.
Постройте: многоугольник распределения; 2. график интегральной функции распределения.
| 1. | Х | |||||
| р | 0,1 | 0,3 | 0,2 | 0,4 |
| 2. | Х | |||||
| р | 0,2 | 0,1 | 0,3 | 0,4 |
| 3. | Х | |||||
| р | 0,4 | 0,1 | 0,3 | 0,2 |
| 4. | Х | |||||
| р | 0,1 | 0,3 | 0,4 | 0,2 |
| 5. | Х | |||||
| р | 0,3 | 0,3 | 0,2 | 0,2 |
| 6. | Х | |||||
| р | 0,2 | 0,5 | 0,2 | 0,1 |
| 7. | Х | |||||
| р | 0,1 | 0,4 | 0,3 | 0,2 |
| 8. | Х | |||||
| р | 0,5 | 0,2 | 0,2 | 0,1 |
| 9. | Х | |||||
| р | 0,2 | 0,4 | 0,3 | 0,1 |
| 10. | Х | |||||
| р | 0,3 | 0,2 | 0,2 | 0,3 |
Методические указания по выполнению работы:
1. Сумма вероятностей для всех значений ДСВ всегда равна единице, т.е. 
2. Математическое ожидание – среднее значение случайной величины – находится по формуле:

3. Дисперсия характеризует степень отклонения значений случайной величины от ее среднего значения. Для вычисления D[X] удобна следующая формула:

4. Среднеквадратическое отклонение σ(Х) находится по формуле: 
|
|
|
5. 
Графики:
1. Многоугольник распределения- набор точек с координатами (х1; р1), (х2; р2)… (хi; рi), последовательно соединенных отрезками ().
2. График интегральной функции распределения имеет ступенчатый вид.
Список литературы:
1.Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учредж. СПО / М.С. Спирина, П.А. Спирин. - М: Изд. центр «Академия», 2012.-Глава 2, п.2.2.., стр.118.
2.Калинина В.Н., Панкин В.Ф.Математическая статистика: учебник для ССУЗов / В.Н. Калинина, В.Ф.Панкин -М: Высш.шк., 2001.–Глава 5, §5.5, стр. 82.
Раздел 3. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Тема 3.3. Законы распределения ДСВ.
Задание 10. Запись распределения и вычисление характеристик для биномиальной и геометрической ДСВ. – 2 ч.
Задание для самостоятельной внеаудиторной работы:
1.Изучите биномиальное и геометрическое распределение ДСВ.
2. Вероятность закатить хотя бы один шар в лузу при одном ударе бильярдиста постоянна и рана 0,7. Если при ударе закатить шар не удается, право удара переходит к другому игроку. Какова вероятность, что бильярдист сделает не менее 4 ударов? Найдите числовые характеристики ДСВ.
3. Охотник-любитель стреляет из ружья по неподвижной мишени. Вероятность попасть в мишень при одном выстреле является величиной постоянной и равна 0,65. Стрельба по мишени ведется до первого попадания. Определить числовые характеристики.
Методические указания по выполнению работы:
Биномиальное распределение.
Если производится n независимых испытаний, в каждом из которых событие А может появится либо не появиться, причем вероятность наступления события в каждом испытании постоянна и равна p, то закон распределения вероятностей определяется формулой Бернулли: 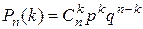 , которое называют биноминальным распределением вероятностей.
, которое называют биноминальным распределением вероятностей.
Запишем биноминальный закон в виде таблицы:
| X | n | n – 1 | … | k | … | |
| Р | pn | npn -1 q | … | 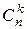 pkqn - k pkqn - k
| … | qn |
|
|
|
 ,
, 
Пример1. Игральная кость брошена 3 раза. Написать закон распределения числа появлений шестерки.
Решение. Вероятность появления шестерки при одном бросании p = 1/6, вероятность непоявления шестерки q = 1 – p = 5/6.
При трех бросаниях игральной кости шестерка может появиться либо 3 раза, либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: x 1 = 0, x 2 = 1, x 3 = 2, x 4 = 3. Найдем вероятности этих возможных значений по формуле Бернулли:  .
.
 ,
,  ,
,
 ,
,  .
.
Искомый закон распределения:
| Х | x 1 | x 2 | x 2 | x 3 |
| Р | 125/216 | 75/216 | 15/216 | 1/216 |
 ,
, 
|
|
|


