 |
Задание 18. Проверка гипотезы о нормальном распределении.– 2 ч.
|
|
|
|
Задание для самостоятельной внеаудиторной работы:
1. Повторите алгоритм проверки гипотезы о нормальном распределении критерием согласия Пирсона.
2. Пользуясь критерием согласия Пирсона при уровне значимости 0,005, проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
| Эмп. частоты | |||||||
| Теор. частоты |
Методические указания по выполнению работы:
Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины – критерия согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Ограничимся описанием применения критерия Пирсона и проверки гипотезы о нормальном распределении генеральной совокупности. С этой же целью будем сравнивать эмпирические (наблюдаемые) и теоретические частоты (вычисленные в предположении нормального распределения).
Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Возможно, что расхождение случайно и объясняется малым числом наблюдений либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.
Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данным наблюдением.
|
|
|
Пусть по выборке объема n получено эмпирическое распределение:
варианты, 
| 
| 
| … | 
|
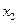
эмп.частоты,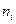 
| 
| 
| … | 
|
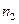
теор.частоты,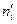 
| 
| 
| … | 
|
Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты 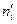. При уровне значимости 
требуется проверить нулевую гипотезу о нормальном распределении генеральной совокупности.
В качестве критерия проверки нулевой гипотезы примем случайную величину
.
Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределения.
Число степеней свободы находят по равенству k=s-1-r, где s – число групп (частичных интервалов) выборки; r – число параметров предполагаемого распределения, которые оценены по данным выборки.
В частности, если предполагаемое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратичное отклонение). Поэтому r =2 и число степеней свободы k=s-1-r =s-1-2=s-3.
Алгоритм применения критерия Пирсона.
1. Определяют теоретические частоты 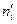, соответствующие опытным частотам. Если среди опытных частот имеются малочисленные, то их необходимо объединить с соседними.
2. По формуле вычисляют величину .
3. Определяем число степеней свободы k= l-3, где l – число интервалов после объединения.
4. Находят уровень значимости 
, где 
– доверительная вероятность.
5.По таблице при заданных и 
находят значение 
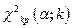, которое является критической точкой.
6. Если 
, нет оснований отвергнуть нулевую гипотезу.
Если 
, нулевую гипотезу отвергают.
Пример 1.
При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
|
|
|
| Эмп. частоты | ||||||||
| Теор. частоты |
Рассчитаем 
, для чего составим расчетную таблицу
|
|
| 
| 
| 
|
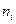
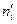
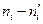
| -1 | 0.07 | ||||
| -4 | 0.38 | ||||
| -8 | 0.78 | ||||
| 0.49 | |||||
| 1.07 | |||||
| -7 | 1.32 | ||||
| 0.08 | |||||
| 7.19 |
Число степеней свободы определим по соотношению k=8–3=5 (в нашем случае s=8). По таблице критических значений при заданных 
и 
находим значение 
.
Так как , то нет оснований отвергать нулевую гипотезу. Расхождение эмпирических и теоретических частот незначимое. Данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
Список литературы:
1.Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учредж. СПО / М.С. Спирина, П.А. Спирин. - М: Изд. центр «Академия», 2012.-Глава 3, п.3.6., стр.221.
|
|
|
