Задание 4. Вычисление вероятностей сложных событий с помощью теорем сложения и умножения вероятностей.– 2 ч.

Задание для самостоятельной внеаудиторной работы:

1.Повторите,основные операции над событиями.Выучите теоремы сложения вероятностей для совместных и несовместных событий, теоремы умножения вероятностей для зависимых и независимых событий, теорему о вероятности противоположного события.

2. В магазин поступило 30 телевизоров, 5 среди которых имеют скрытые дефекты. Наудачу отбираются 2 телевизора для проверки. Какова вероятность того, что оба они не имеют дефектов?

3. Вероятность безотказной работы двух независимо работающих сигнализаторов равна 0.6 и 0.7. Найти вероятность того, что сработают: а) оба сигнализатора, б) хотя бы один сигнализатор.

4. Изделия проверяются на стандартность. Вероятность того, что изделие стандартно равна 0.8. Найти вероятность того, что из двух проверенных изделий только одно стандартно.

5. В экзаменационном билете три вопроса, Вероятность ответа на первый вопрос - 0.9; на второй - 0.7; на третий - 0.5. Найти вероятность различных оценок.

6. Студент знает 20 вопросов из 25-ти. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.

7. Брошены монета и игральная кость. Найти вероятность совмещения событий: «появился герб», появилось 6 очков».

8. Вероятности поражении цели первым стрелком равна 0,8, вторым 0,6. Найти вероятности следующих событий: а) цель поражена двумя попаданиями; б) одним выстрелом; в) цель не поражена.

9. В урне находится 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар, при втором черный и при третьем – синий.

101. В урне 7 белых и 9 красных шаров. Из урны наугад вынимают первый шар, определяют цвет. Затем второй шар. Найдите вероятность, что они оба белые.

10.2. Из урны (задача 10.1) одновременно вынимают два шара. Найдите вероятность того, что они оба белые. (Это разные задачи?)

Методические указания по выполнению работы:

Суммой А + В событий называется событие, состоящее в том, что в результате опыта наступит или событие А, или событие В, или оба вместе. (Другими словами, суммой А+В событий А и В называется событие, состоящее в появлении хотя бы одного из этих событий):

Если события А и В несовместны, то А + В – это событие А, или событие В.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Произведением АВ событий А и В называется событие, состоящее в совместном появлении и события А, и события В.

Произведением нескольких событий называется событие, состоящее в их совместном появлении.

Событием, противоположным событию А, называется событие, обозначаемое и состоящее в том, что в результате опыта событие А не наступит.

 

Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Следствие1. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А₁ + А₂+ …+ А_n) = P(A₁) + P(A₂)+ P(A₃) + …+ P(A_n).

Следствие 2. Если события А₁, A₂, A₃, …An образуют полную группу событий, то сумма их вероятностей равна единице: P(A₁) + P(A₂)+ P(A₃) + …+ P(An) = 1.

Следствие 3. Сумма вероятностей противоположных событий равна единице:

P(A) + P() = 1.

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A + B) = P(A) + P(B) – P(AB).

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Несколько событий называются независимыми в совокупности, если любое из них не зависит от любой совокупности остальных.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло это событие В или нет.

Вероятность события А, вычисляемая при условии, что событие В произошло, называется условной вероятностью события а и обозначается P_B(A)

 

Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению одного из них на условную вероятность другого, вычисленную при условии, что первое из них произошло:

P(AB) = P(A)P_A(B) = P(B)P_B(A).

Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

P(AB) = P(A)P(B).

Для вычисления вероятности совместного появления большего числа событий, например, четырех, используют формулу:

P(ABCD) = P(A)P_A(B)P_AB(C)P_ABC(D).

Для нескольких независимых в совокупности событий вероятность их произведения равна произведению их вероятностей:

P(A₁A₂…A₃) = P(A₁)P(A₂)…P(A_n).

Следствие 3. Вероятность появления хотя бы одного из событий А₁,A₂…A_n., независимых в совокупности, равна разности единицы и произведения вероятностей противоположных событий ₁, ₂,… _n: PA₁ + A ₂ + …A_n) = 1 – P( ₁) P( ₂)… P( _n)

 

Пример 1. В урне 20 шаров: 8 красных, 6 синих, 6 белых. Найти вероятность появления цветного шара.

Решение. Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного Р (А) = 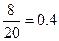, синего Р (В) = . События А и В несовместны, по теореме сложения:

Пример 2. Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны P 1 = 0,8, P 2 = 0,9. Найти вероятность попадания при одновременном залпе (из обоих орудий) хотя бы одним из орудий.

Решение. По условию события А (попадание первого орудия) и В (попадание второго орудия) совместны и независимы. Вероятность того, что оба орудия попали

P (AB) = P (A)× P (B) = 0,8×0,9 = 0,72.

Вероятность попадания при одновременном залпе хотя бы одним из орудий

P (A + B) = P (A) + P (B) – P (AB) = 0,8 + 0,9 – 0,72 = 1,7 – 0,72 = 0,98.

 

Пример 3. Пример. В типографии имеется 3 машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,8. Найти вероятность того, что в данный момент работает хотя бы одна машина.

Решение. Событие А – машина работает, противоположное событие Ā – машина не работает. Эти события образуют полную группу.

p + q = 1, q = 1 – p = 0,2, Р (А) = 1 – qⁿ = 1 – 0,2³ = 0,992.

Пример 4. Пример. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.

Решение. Событие А ₁ – извлечение белого шара при первом испытании, А ₂ – извлечение белого шара при втором испытании. Эти события совместны, следовательно извлечение двух белых шаров А = А ₁× А ₂. Всего в урне 5 шаров. Вероятность извлечение белого шара при первом испытании Р (А ₁) = 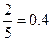, вероятность извлечение белого шара при втором испытании при условии, что при первом испытании был извлечен белый шар .

По теореме умножения совместных событий Р (А) = Р (А ₁ А ₂) = Р (А ₁) Р_{А 1}(А ₂) = .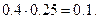

 

Пример 5. Производится три выстрела по одной и той же мишени. Вероятность попадания при первом, втором и третьем выстрелах равна Р ₁= 0,4; Р ₂ = 0,5; Р ₃ = 0,7. Найти вероятность того, что в результате этих трех выстрелов произойдет ровно одно попадание.

Решение. Событие А – ровно одно попадание в мишень; А ₁, А ₂, А ₃ – попадание при первом, втором и третьем выстрелах соответственно; Ā ₁, Ā ₂, Ā ₃ – промах при первом, втором и третьем выстрелах соответственно. Событие А может наступить, если первый стрелок попал, а второй и третий не попали А ₁ Ā ₂ Ā ₃; если второй стрелок попал, а первый и третий не попали Ā ₁ А ₂ Ā ₃; если третий стрелок попал, а первый и второй не попали Ā ₁ Ā ₂ А ₃:

А = А ₁ Ā ₂ Ā ₃ + Ā ₁ А ₂ Ā ₃ + Ā ₁ Ā ₂ А ₃.

Искомая вероятность

Р (А) = Р (А ₁ Ā ₂ Ā ₃) + Р (Ā ₁ А ₂ Ā ₃ ) + Р (Ā ₁ Ā ₂ А ₃);

Р (А) = Р (А ₁)× Р (Ā ₂)× Р (Ā ₃) + Р (Ā ₁)× Р (А ₂)× Р (Ā ₃) + Р (Ā ₁)× Р (Ā ₂)× Р (А ₃);

Р (А) = 0,4×0,9×0,3 + 0,6×0,9×0,3 + 0,6×0,9×0,7 = 0,06 + 0,09 + 0,21 = 0,36.

 

Список литературы:

1.Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учредж. СПО / М.С. Спирина, П.А. Спирин. - М: Изд. центр «Академия», 2012.-Глава 1, п.1.6., стр.34.

2.Калинина В.Н., Панкин В.Ф.Математическая статистика: учебник для ССУЗов / В.Н. Калинина, В.Ф.Панкин -М: Высш.шк., 2001.–Глава 3, §3.1 – 3.2, стр. 42.

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: