 |
Дифференциал второго порядка
|
|
|
|
Определение 1(дифференциал второго порядка). Значение δ(d y) дифференциала от первого дифференциала (5) при δ x = d x, называется вторым дифференциалом функции y = f (x) и обозначается d2 y.
Таким образом,
d 2 y = δ (dy) | δ x = dx .
Дифференциал dn y можно ввести по индукции.
Определение 7. Значение δ(dn-1 y) дифференциала от(n- 1)-го дифференциала при δ x = d x, называется n- м дифференциалом функции y = f (x) и обозначается dn y.
Найдем выражение для d2 y при этом рассмотрим два случая, когда x -независимая переменная и когда x = φ(t), то есть является функцией переменной t.
1. пусть x = φ(t), тогда
d 2 = δ (dy) | δ x = dx = δ(f' (x) dx) | δ x = dx =
= {δ(f' (x)) dx+f' (x)δ(dx)} | δ x = dx = f'' (x)(dx)2 +f' (x) d 2 x.
Итак,
| d 2 y = f'' (x)(dx)2 +f' (x) d 2 x. | (7) |
2. пусть x - независимая переменная, тогда
d 2 y = f'' (x)(dx)2,
так как в этом случае δ(dx) = (dx)'δ x = 0.
Аналогично, по индукции легко получить следующую формулу, если x - независимая переменная:
dny = f (n)(x)(dx) n.
Из этой формулы следует, что f(n) = dny/(dx)n.
В заключение отметим, что дифференциалы второго и более высоких порядков не обладают свойством инвариантности, что сразу видно из формулы для дифференциала второго порядка (7).
Интегральное исчисление функции одной переменной
Неопределенный интеграл.
Функция 
называется первообразной по отношению к функции 
, если дифференцируема и выполняется условие
.
Очевидно, что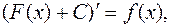 
где С-любая константа.
Неопределенным интегралом от функции называется множество всех первообразных этой функции. Неопределенный интеграл обозначается 
и равен
.
Основные свойства неопределенного интеграла
1. 
dF(x) = F(x)+C. Справедливость этого равенства следует из очевидной цепочки равенств
dF (x) = F' (x) dx = f (x) dx = F (x) +C.
|
|
|
2. d f(x)dx = f(x)dx. Данная формула следует из равенства
d f (x) dx = d (F (x) +C) = dF (x) = F' (x) dx = f (x) dx.
3. Если функции f1(x), f2(x) имеют первообразные, то функция f1(x)+f2(x) тоже имеет первообразную, причем
(f 1(x) +f 2 (x)) dx = f 1(x) dx+ f 2(x) dx.
4. Если функция f(x) имеет первообразную и k– постоянная, то и функция kf(x) также имеет первообразную, причем при k≠0 справедливо равенство kf (x) dx = k f (x) dx.
Заметим, что свойства 3 и 4 следуют из свойств производной.
Основные правила интегрирования.
1. 
, 
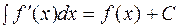, где С – произвольная постоянная.
2. 
, где А- постоянная величина.
3. 
.
4. Если и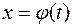 
- дифференцируемая функция, то 
.
Таблица основных интегралов.
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
| 
| |||
|
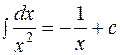
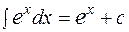
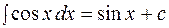
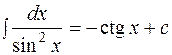
Основные методы интегрирования.
1. Непосредственное интегрирование
Это нахождение неопределенного интеграла с помощью его свойств, тождественных преобразований подынтегральной функции и таблицы основных интегралов.
2. Введение под знак дифференциала.
Этот метод используется для интегрирования сложных функций и заключается в том, что аргумент сложной функции записывается под знаком дифференциала. После введения аргумента под знак дифференциала нужно разделить подынтегральное выражение на производную этого аргумента. Цель метода введения под знак дифференциала, как и метода непосредственного интегрирования, привести исходный интеграл к табличному.
3. Метод замены переменной (подстановки)
Требуется найти интеграл: , причем, непосредственно подобрать первообразную для нельзя, но известно, что она существует. Положим 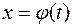, где 
-непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда 
и справедливо равенство:
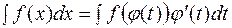
Это и есть формула метода замены переменной или метода подстановки. Этот метод является одним из основных методов интегрирования. Его задача – свести заданный интеграл к табличному или к более простому, который затем уже приводится к одному или нескольким табличным интегралам.
|
|
|
|
|
|
