 |
Исследование математических моделей
|
|
|
|
Регрессионный анализ
Под регрессионным анализом понимают исследование связей между входными X и выходными Y значениями изучаемого процесса, которые зависят от многих, иногда неизвестных факторов. Для выявления этих связей проводят экспериментальные исследования.
По результатам эксперимента строят модель процесса в виде уравнения регрессии
(1)
где G(x) - расчётное значение функции; g1(x)…gk(x) - простые (элементарные) функции; С1…Ск - коэффициенты регрессии.
В частных случаях используют линейную регрессию
(2)
степенной полином
(3)
полином второго порядка для n-мерного пространства
. (4)
Простые функции gk(x) уравнения (1) подбирают по виду экспериментальных кривых. Данные измерений наносят на сетку прямоугольных координат, соединяют экспериментальные точки плавной кривой и подбирают ориентировочно вид функции.
Функции должны быть по возможности наиболее простыми и соответствовать экспериментальным данным в пределах изменений аргумента.
Подбор коэффициентов регрессии
Если все m измерения функций y1, y2,…yj (рис.1) произведены с одинаковой точностью, и распределение величин ошибок измерений 
соответствует нормальному закону, то параметры регрессионного уравнения определяют из условия, при котором сумма квадратов отклонений измеренных средних значений 
от расчетных G(xi) принимают наименьшее значение.
Этот метод называют методом наименьших квадратов.
(5)
Рис. 1. Результаты эксперимента
Математически условие min суммы квадратов можно найти, приравнивая к нулю частные производственные по коэффициентам регрессии.
; 
; 
; (6)
где k – количество коэффициентов регрессии в уравнении.
В общем виде.
|
|
|
; (7)
Подставив в выражение (1.7) значение G(x) (1.1) получим систему нормальных уравнений
(8)
Из системы линейных алгебраических уравнений (8) определяют все коэффициенты Сk. Матрицу этой системы называют матрицей Грама
(9)
Поскольку коэффициенты регрессии рассчитывают по результатам опытов, являющихся случайными величинами, то и сами коэффициенты носят случайный характер.
В общем случае эти коэффициенты имеют разные дисперсии и разную величину взаимной корреляции.
Оценка адекватности модели
Установление адекватности – это определение ошибки аппроксимации опытных данных. Методы оценки адекватности основаны на использовании доверительных интервалов, позволяющих с заданной доверительной вероятностью определять искомые значения оцениваемого параметра. В практике оценки адекватности применяют различные критерии согласия.
Одним из таких критериев является критерий Фишера. Рассчитывают экспериментальное (опытное) значение критерия Фишера – kфэ и сравнивают его с теоретическим (табличным) – kф т, принимаемым при требуемой доверительной вероятности pд (обычно pд = 0,95). Если kфэ < kф т – модель адекватна; если kфэ ³ kф т – модель неадекватна. Экспериментальный критерий Фишера вычисляют по формуле
, (10)
где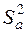 
– оценка дисперсии адекватности (модели); 
– оценка средней дисперсии эксперимента (данных).
Оценка дисперсии адекватности
, (11)
оценка дисперсии эксперимента для i – ой точки (рисунок 1.1)
, (12)
оценка средней дисперсии эксперимента в целом, при одинаковых повторностях опытов
, (13)
где 
- число степеней свободы; 
- теоретическое значение функции для каждого измерения; 
- среднее экспериментальное значение функции из n серий опытов; m - количество измерений в одной серии опытов; 
- экспериментальное значение функции.
Значение kф т принимается для числа степеней свободы n1 = n – d, n2 = n(m – 1).
|
|
|
