 |
Нелинейные оптимизационные модели с ограничениями
|
|
|
|
Решение многих инженерных задач сводится к отысканию наилучшего (оптимального) решения технической или организационной проблемы.
Задача оптимизации в общем виде формулируется следующим образом: найти минимум функции f(х), n - мерного векторного аргумента х.
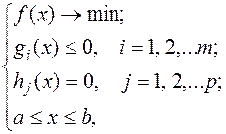(33)
где f(x) – целевая функция или критерий оптимальности; x = (x1, x2,…xn)T – вектор параметров n -мерного пространства; gi(x) и hj(x) – функции ограничений неравенств и равенств; a и b – ограничения.
При наличии ограничений задачу называют задачей условной оптимизации, при отсутствии ограничений – задачей безусловной оптимизации.
Ограничения, наложенные на переменную х, называют явными, а на функции f(х) - неявными.
Каждая точка х в n -мерном пространстве переменных хi,…хn, в котором выполняются ограничения задачи, называется допустимой точкой задачи. Множество всех допустимых точек называется допустимой областью G. Решением задачи считается допустимая точка х, в которой целевая функция f(х) достигает своего минимального значения. Если целевая функция f(х) и ограничения задачи представляют собой линейные функции независимых переменных хi,…,хn, то соответствующая задача является задачей линейного программирования, в противном случае - задачей нелинейного программирования.
В общем случае численные методы оптимизации можно разделить на прямые и непрямые. Прямые методы оперируют непосредственно с исходными задачами оптимизации и генерируют последовательности точек (х [ k ]), таких, что f(x [ k+1 ] < f (x [ k ]). В силу этого такие методы часто называют методами спуска. Математически переход на некотором k -ом шаге (k =0,1,…) от точки x [ k ] к точке x [ k+1 ] записывается в следующем виде:
|
|
|
, (34)
где р [ k ] - вектор, определяющий направление спуска; ак - длина шага вдоль данного направления.
Различные методы спуска отличаются друг от друга способами выбора двух параметров – направления спуска и длины шага вдоль этого направления.
В методах спуска решение задачи теоретически получают за бесконечное количество итераций. На практике вычисления прекращают при выполнении некоторых условий, например малости приращения аргумента
(35)
или функции
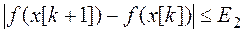, (36)
где E1 и E2 – заданные величины точности вычислений.
В зависимости от вида используемой информации методы минимизации подразделяются на методы нулевого порядка, методы первого порядка, методы второго порядка.
В методах нулевого порядка для определения направления спуска не требуется вычислять производные целевой функции. Направление минимизации полностью определяется последовательными вычислениями значений целевой функции.
Методы первого порядка основаны на вычислении первой производной целевой функции. В данном методе направление поиска p [ k ] выбирается в сторону наибольшего уменьшения функции, т.е. в направлении противоположном grad f(x). Итерационный процесс записывают в виде
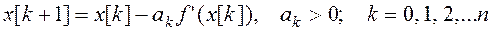(37)
Методы первого порядка называют также градиентными методами.
Методы оптимизации второго порядка используют вторые частные производные минимизируемой функции f(x).
Необходимым условием экстремума функции многих переменных f(x) в точке x является равенство нулю ее градиента в этой точке. Итерационный процесс описывается выражением
, (38)
где H-1(x [ k ] ) – обратная матрица для матрицы вторых производных Гессе f”(x [ k ] ); -H-1(x [ k ] )f’(x [ k ] ) = p [ k ] - направление спуска.
Непрямые методы сводят исходную задачу нелинейного программирования к последовательности задач безусловной оптимизации некоторых вспомогательных функций. При этих методах ограничения исходной задачи учитываются в неявном виде.
|
|
|
Вопросы для зачета
1 Классификация моделей.
2 Виды подобия модели и оригинала.
3 Познавательные и прагматические модели.
4 Классификация математических моделей.
5 Требования к моделям.
6 Что такое адекватность?
7 Математические модели на мега уровне. Уравнение регрессии.
8 Особенности математических моделей на микро уровне.
9 Математические модели переходных процессов в электрических цепях. Дифференциальные уравнения. Начальные условия.
10 Численные методы, используемые для моделирования переходных процессов на ЭВМ. Метод Эйлера.
11 Конечные разности и разностные уравнения. Как от дифференциального уравнения перейти к разностному уравнению?
12 Метод сеток. Основная идея.
13 Как составить разностные уравнения.
14 Оптимизация. Постановка задачи.
15 Классификация оптимизационных задач.
16 Приведите пример оптимизационной задачи (по специальности).
17 Методы оптимизации первого порядка. Общая характеристика. Область применения.
18 Методы оптимизации второго порядка. Характеристика. Область применения.
19 Методы нулевого порядка. Характеристика. Достоинства и недостатки.
20 Метод золотого сечения.
21 Комплексный метод Бокса. Алгоритм.
Литература
1. Банди Б. Методы оптимизации. Вводный курс. - М.: Радио и связь, 1988.- 80 с.
2. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. - М.: Высшая школа, 1978.-282 с.
3. Дьяконов В.П. Математическая система Maple V R3/R4/R5. – М.: “Солон”, 1998. – 399 с.
4. Калинина В.Н., Панкин В.Ф. Математическая статистика. - М.: Высшая школа, 1994. – 336 с.
5. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1973. – 726 с.
6. Мжельский Б.И., Мжельская Е.Б. Основы теории оптимизации: Учебное пособие. – М.: Издательство МЭИ, 2001. – 80 с.
7. Мудров А.Е. Численные методы для ПЭВМ на языке Бейсик, Фортран и Паскаль. - Томск: МП "РАСКО", 1991. – 272 с.
8. Основы научных исследований: Учеб. для техн. вузов/ В.И. Крутов, И.М. Грушко, В.В. Попов и др. – М.: Высш. шк. 1989. – 400 с.
9. Перегудов И.Ф., Тарасенко Ф.П. Введение в системный анализ: Учебное пособие для вузов. - М.: Высшая школа, 1989.- 367 с.
10. Фурунжиев Р.И., Бабушкин Ф.М., Варавко В.В. Применение математических методов и ЭВМ: Практикум: Учебное пособие для вузов. - Мн.: Высшая школа, 1988. – 191 с.
|
|
|
 |
|
|
|
