Моделирование нестационарных электрических и тепловых полей

 

Для исследования тепловых и электрических полей формулируют и решают краевую задачу, содержащую дифференциальные уравнения в частных производных (24) и граничные условия, определяющие законы изменения исследуемой величины на границах задачи.

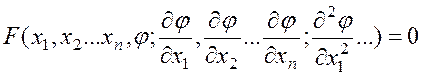(24)

Для численного решения дифференциальных уравнений в частных производных широко применяется метод конечных разностей (метод сеток). Область непрерывного изменения аргументов x, y, z, t в этом методе заменяется сеткой – конечным (дискретным) множеством точек, называемых узлами. Разности значений аргументов для двух смежных узлов D x, D y, D z, D t называют шагами изменения этих аргументов.

Дифференциальное уравнение заменяется на сетке разностной схемой или уравнением в конечных разностях. Получают систему алгебраических уравнений с числом неизвестных, равным числу узлов сетки. Если исходное дифференциальное уравнение линейное, то задача состоит в решении системы линейных алгебраических уравнений. Если же исходное дифференциальное уравнение нелинейно, задача сводится к решению системы нелинейных алгебраических или трансцендентных уравнений.

Пусть у=у(х_i) функция переменного х. Для заданных значений аргумента х

и соответствующих значений функции у

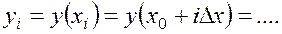
конечные разности записываются в следующем виде

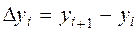
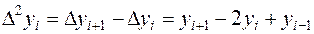(25)

……………………………………………

Используя конечные разности производные дифференциальных уравнений можно записать в разностной форме.

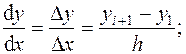(26)

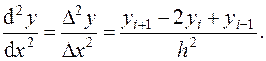
Важнейшими свойствами разностных схем являются аппроксимируемость, устойчивость и сходимость.

Аппроксимируемость схемы означает, что при стремлении к нулю шагов аргументов решение системы алгебраических уравнений стремится к решению исходного дифференциального уравнения при заданных граничных условиях.

Устойчивой называют такую схему, для которой ошибки округления, неизбежные при любых расчетах, при уменьшении шагов аргументов (сгущении сетки) не приводят к большим искажениям решения. В противном случае схема называется неустойчивой.

Сходимость схемы означает, что при сгущении сетки решение системы алгебраических уравнений приближается (сходится) к решению исходного дифференциального уравнения при заданных граничных условиях. Сходимость – следствие одновременных аппроксимируемости и устойчивости.

Различают явные и неявные разностные схемы. В явных схемах значение в очередном в узле сетки 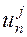вычисляют через найденные ранее значения . Алгоритм численного расчета по явной схеме легко программируется. Однако явная схема условно устойчива, т.е. устойчива при определенном ограничении величины шага во времени Dt (рис. 3).

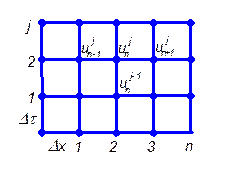
Рис. 3. Разностная схема

В неявных схемах в уравнение для отыскания значения в узле сетки 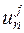входят неизвестные значения в соседних (n – 1) и (n + 1) узлах сетк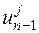и и . Таким образом, в каждом временном слое значение в узле сетки определяется из решения системы уравнений. Количество уравнений в системе равняется количеству узлов расчетной сетки. Неявная схема безусловно устойчива, т.е. устойчива при любых значениях шага Dt.

В качестве примера неявной схемы рассмотрим задачу об определении электрического потенциала в бесконечном желобе прямоугольного сечения (рис.4).

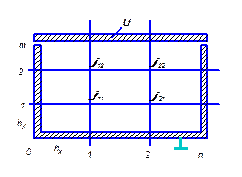
Рис. 4. Определение электрического потенциала

Верхняя стенка желоба имеет потенциал U, остальные стенки заземлены. Необходимо найти распределение потенциала в прямоугольной области (внутри стенки).

Распределение потенциала в замкнутом объеме при отсутствии объемных электрических зарядов удовлетворяет уравнению Лапласа.

(27)

в прямоугольной системе координат уравнение Лапласа имеет вид

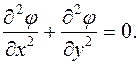(28)

Разобьем область определения потенциала прямоугольной сеткой с помощью прямых х = х_i, у = у_i. Шаг сетки выбирается в соответствии с требуемой точностью вычислений.

Запишем уравнение Лапласа (28) в конечных разностях

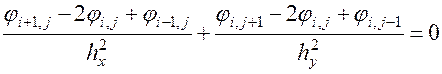. (29)

при условии 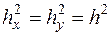выражение (29) можно преобразовать к виду

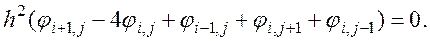(30)

Записывая разностное уравнение (30) для узлов сетки j_i,j (i = 0…n; j = 0…m; n=3; m=3) c учетом граничных условий

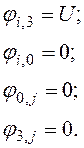(31)

задача будет сведена к системе алгебраических уравнений с (m-1)*(n-1) неизвестными

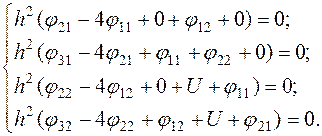(32)

Для упрощения замены в узлах сетки (i, j) производных дифференциального уравнения разностными уравнениями используют шаблоны (разностные операторы) (рис. 5).

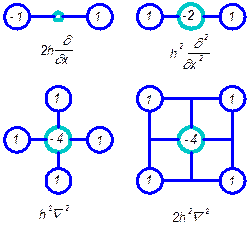
Рис. 5. Разностные операторы

 

Под каждым шаблоном указан порядок дифференциального уравнения, с которым он может быть использован.

Шаблон устанавливают выделенным участком на тот узел сетки, для которого записывают разностное уравнение. В кружочках шаблона указаны весовые коэффициенты используемых узлов сетки.

Так для узла j₁₁ с использованием шаблона h² Ñ ² можно записать

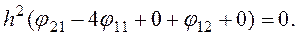
Последовательно устанавливая шаблон на каждый узел сетки, получают систему алгебраических уравнений, которая решается известными методами.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: