 |
Моделирование переходных процессов
|
|
|
|
Переходными процессами называют переход физических систем из одного состояния в другое, бесконечно близкое. Примерами таких процессов могут служить явления, возникающие в электрических цепях, распространение радиоволн, явления химической кинетики, сопротивления материалов, движения материальных точек и т. д.
Математические модели переходных процессов составляют с использованием обыкновенных дифференциальных уравнений или системы таких уравнений.
Дифференциальным называется уравнение, содержащее неизвестные функции у, независимые переменные х и производные неизвестных функций у’, у”,…, у(n):
 (14)
(14)
Дифференциальное уравнение называют обыкновенным, если неизвестные функции зависят от одной независимой переменной х. Если неизвестные функции зависят от нескольких независимых переменных, дифференциальное уравнение носит название уравнения с частными производными. Порядок дифференциального уравнения определяет наивысший из порядков производных, входящих в уравнение. Совокупность уравнений, содержащих несколько неизвестных функций и их производных, образует систему дифференциальных уравнений.
Решить дифференциальное уравнение – значит найти его общий интеграл. Под общим интегралом понимают соотношение между независимой переменной, зависимой переменной и произвольными постоянными, число которых равно порядку дифференциального уравнения. Это соотношение при всех допустимых значениях независимой переменной должно удовлетворять данному дифференциальному уравнению. Общий интеграл геометрически выражается семейством кривых. Для выделения одной кривой из этого семейства, т.е. для получения частного решения, необходимо определить произвольную постоянную, задавшись начальными условиями. В уравнениях n -го порядка эти условия задаются значения у, у’,…,у(n-1) при х=х0:
|
|
|
 (15)
(15)
Дифференциальное уравнение считается разрешенным относительно старшей производной, если оно приведено к виду
 (16)
(16)
Отыскание решения этого уравнения при заданных начальных условиях называется задачей Коши для обыкновенного дифференциального уравнения.
Любое уравнение n -го порядка можно свести к системе n уравнений первого порядка способом замены переменных. Для этого вводят новые переменные у’=у1, у”=у2,…,у(n-1)=уn-1, в результате чего получают эквивалентную систему:
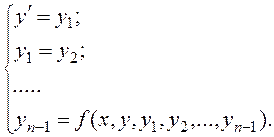 (17)
(17)
Указанный прием позволяет свести решение дифференциального уравнения n-го порядка к решению системы n уравнений первого порядка. В свою очередь методы решения одного уравнения первого порядка распространяются на систему таких уравнений.
Аналитические методы решения дифференциальных уравнений позволяют выразить решение через элементарные или специальные функции. Однако классы уравнений, для которых разработаны точные методы решения, довольно узки и охватывают только малую часть возникающих на практике задач. В силу этого важное значение имеют приближенные численные методы решения, ориентированные на широкий класс встречающихся в практике дифференциальных уравнений.
Для численного решения дифференциальных уравнений применяются одношаговые и многошаговые методы. Одношаговым называется метод, в котором для расчета следующей точки требуется информация только о последней вычисленной точке. В многошаговых методах для расчета следующей точки используются данные решения на нескольких предшествующих шагах. Примерами таких методов могут служить методы прогноза и коррекции.
Из одношаговых методов решения обыкновенных дифференциальных уравнений наиболее распространены методы Рунге-Кутта.
|
|
|
Различные методы данной группы отличаются друг от друга объемом вычислений и точностью решения. Метод Рунге-Кутта первого порядка называют обычно методом Эйлера.
Метод Эйлера основан на разложении у ’в ряд Тейлора в окрестностях точки х0
 . (18)
. (18)
Для этого производная у’ заменяется приближенной формулой
 . (19)
. (19)
В результате, на первом отрезке [ х0, х1 ] искомое решение приближенно представляется линейной функцией
 (20)
(20)


При х=х1 получаем
 (21)
(21)
Иными словами, на отрезке [ х0,у0 ] искомая интегральная кривая (точное решение) заменяется отрезком прямой М0-М1, касательными к кривой в точке М0 (рис. 2).

Рис. 2. Геометрическая интерпретация метода Эйлера
Тангенс угла наклона этой прямой равен f(х0, у0). Аналогично находятся остальные приближенные значения:
 (22)
(22)
где 
Таким образом, искомая интегральная кривая заменяется ломанной линией с вершинами в точках 
 …,
…, 
Метод Эйлера является наиболее простым, но и наименее точным численным методом решения дифференциальных уравнений.
В методах Рунге-Кутта более высокого порядка (повышенной точности) каждую последующую точку находят через промежуточные, в каждой из которых определяется направление касательной. В итоге смещение из точки (хi, уi) в (хi+1, уi+1) выполняется вдоль некоторого усредненного направления.
Существуют методы Рунге-Кутта различного порядка, наибольшее распространение среди которых получил метод четвертого порядка. В этом методе величину уi+1 вычисляют по следующим формулам:
 (23)
(23)
где 



|
|
|


