 |
Понятие о математическом моделировании
|
|
|
|
Геологических объектов
1.2.1. Принцип и операции математического моделирования
Любые методы обработки экспериментальных данных содержат в своей основе явную или неявную модель изучаемого объекта или происходящего с ним явления (события).
Математическая модель – это совокупность представлений, предположений, гипотез и аксиом, отражающих существо изучаемого геологического объекта или явления.
Модель выражается в математической форме и позволяет описывать, анализировать и прогнозировать свойства геологических объектов или последствия явлений.
В основе математического моделирования лежит принцип системного подхода. Для исследования выделяются объект или группа однопорядковых объектов, которые рассматриваются как отдельная система, имеющая какие-то физические или условные границы и внутренние связи между частями или свойствами. Геологические объекты, расположенные за пределами системы, являются по отношению к ней окружающей средой.
Когда система определена, осуществляется ее исследование путем математического моделирования. Конечной целью моделирования может быть описание и классификация объектов, понимание геологической природы объектов и явлений, предсказание (прогнозирование) поведения или свойств системы, а в некоторых случаях и управление системой на основе контроля ее состояния. Например, при разведке и эксплуатации месторождения необходимо понять его строение и происхождение, прогнозировать количество и качество минерального сырья, управлять процессом эксплуатации с целью рационального использования недр и решать много других практических задач.
Математическое моделирование геологических объектов можно разделить на несколько последовательных операций:
|
|
|
1. Определение системы, т.е. задание границ, перечня геологических объектов и их свойств, а иногда и характера взаимосвязей между свойствами.
2. Измерение характеристик свойств геологических объектов, входящих в систему. Иначе говоря, получение исходных данных для математической обработки. В некоторых задачах измерения могут отсутствовать, а изучению подвергаются предполагаемые значения, заданные исследователем.
3. Создание геологического представления (геологической модели) о существе изучаемой системы и формулировка геологической задачи, стоящей перед математическим моделированием. Часто можно выдвинуть несколько гипотез о системе, иногда взаимоисключающих друг друга. Тогда на основе последующего математического моделирования можно сделать заключение о том, какая из гипотез более соответствует действительности.
4. Выражение геологических представлений в математической форме, т.е. в виде формул, правил, уравнений и пр. Это и есть математическая постановка задачи. В процессе постановки часто приходится возвращаться к п.2 и 3 для уточнения недостающих сведений.
5. Исследование математической модели, которое чаще всего сводится к решению составленных в п.4 формул и уравнений и вычислению прогнозных значений свойств или параметров явлений, т.е. к получению ответа на геологическую задачу. Если исходные данные колеблются в некоторых пределах, то можно исследовать зависимость прогнозных значений от исходных данных. В некоторых случаях оценивается погрешность прогнозирования.
6. Проверка соответствия полученных результатов фактическим данным. В результате проверки можно определить, насколько правильно математическая модель описывает систему, насколько верны геологические представления, положенные в ее основу. Чаще всего оценивается степень совпадения или сходства фактических данных с теоретическими, вычисленными в ходе решения математической модели. Если имеется несколько геологических и соответствующих им математических моделей, то проверка может дать ответ на вопрос, какая из моделей лучше соответствует действительности. Следует отметить, что проверка не всегда возможна, особенно в тех случаях, когда получение фактических данных затруднено или невозможно.
|
|
|
В зависимости от постановки задачи в результате математического моделирования могут быть получены различные ответы. Во-первых, можно определить прогнозные значения тех свойств, которые трудно измерить или которые не поддаются непосредственному измерению. Во-вторых, можно оценить степень соответствия математической модели фактическим данным. В-третьих, можно установить, какая из математических и, соответственно, геологических моделей лучше соответствует действительности и тем самым выбрать для дальнейших исследований наилучшую модель.
Геологические системы являются весьма сложными структурами, находящимися под влиянием большого числа трудно учитываемых факторов, поэтому математическое моделирование не может дать их исчерпывающую характеристику. Следовательно, любая математическая модель является приближенным отражением реальных природных систем и для каждой природной системы можно построить несколько математических моделей различной степени сложности. Обычно по мере усложнения математической модели повышается достоверность прогнозирования и надежность выводов. Но существует оптимальная степень сложности математических моделей, такая, при которой дальнейшее усложнение не будет повышать достоверность прогнозирования и может даже ухудшить работоспособность модели. Нередко степень сложности математических моделей ограничивается техническими возможностями вычислительной техники.
1.2.2. Примеры математических моделей
Последовательность операций математического моделирования можно показать на нескольких примерах.
8Пример 1.1. Рудное тело имеет длину по простиранию a = 500 м, по падению b = 200 м, видимую среднюю мощность на дневной поверхности m = 8 м, угол падения a = 65°. Необходимо оценить объем рудного тела.
|
|
|
Из условия задачи понятно, что определена система (объект исследования) – рудное тело, измерены его параметры: размеры по простиранию и падению, мощность и угол падения, т.е. выполнены две операции моделирования.
Наиболее ответственна третья операция – создание геологической модели рудного тела. Возможно несколько альтернативных вариантов предположений о форме рудного тела:
а) рудное тело сохраняет протяженность и мощность на глубине, т.е. имеет форму параллелепипеда;
б) рудное тело выклинивается на глубине в линию, т.е. имеет форму клина;
в) рудное тело выклинивается на глубине в точку, т.е. имеет форму пирамиды.
Возможны и другие предположения о форме рудного тела на глубине. При существующем объеме геологической информации сделанные предположения о форме рудного тела равновероятны.
Четвертая операция – это выражение в виде математических формул геологических предположений о форме рудного тела. Предварительно необходимо уточнить, как ориентирована видимая мощность. Положим, что она горизонтальная, тогда истинная мощность рудного тела m ист = m sina. Запишем три формулы объема:
а) объем параллелепипеда V = abm sina;
б) объем клина V = 1/2 abm sina;
в) объем пирамиды V = 1/3 abm sina.
Из сравнения формул видно, что объем рудного тела существенно зависит от предположения о его форме, различаясь по вариантам в 3 раза.
Пятая операция – вычисление (прогнозирование) объема рудного тела по приведенным формулам:
а) объем параллелепипеда V = 725,0 тыс.м3;
б) объем клина V = 362,5 тыс.м3;
в) объем пирамиды V = 241,7 тыс.м3.
Шестая операция – проверка совпадения вычисленного и фактического объемов. Очевидно, что фактический объем рудного тела установить трудно. Это требует проведения дополнительных работ, например детального изучения рудного тела на глубине с помощью разведочных выработок или добычи руды. Предположим, что рудное тело добыто и его объем оказался 350 тыс.м3, тогда можно заключить, что ближе всего к истине второй вариант (выклинивание рудного тела в линию). Погрешность прогнозирования объема рудного тела по второму варианту в абсолютном выражении δ = 362,5×350 = = 12,5 тыс.м3, в относительном 12,5/350 = 0,036 = 3,6 %.7
|
|
|
8 Пример 1.2. В рудах полиметаллического месторождения пробы проанализированы на цинк и кадмий. При построении графика обнаружено, что с возрастанием содержаний цинка растет содержание кадмия (рис.1.1). Требуется дать геологическое объяснение зависимости и построить математическую модель.
|
Исходными данными для построения модели являются содержания цинка x и кадмия y в пробах руды. Пока не будем рассматривать конкретные числовые данные и их обработку, а ограничимся логическими рассуждениями.
Зависимость между содержаниями цинка и кадмия вызвана тем, что оба компонента входят в состав одного минерала – сфалерита. При увеличении количества сфалерита растет содержание цинка и кадмия в руде. Это предполагаемая геологическая модель зависимости.
Математическая модель сводится к составлению уравнения зависимости между содержаниями цинка и кадмия. Пренебрегая неизбежными колебаниями состава сфалерита, можно принять, что содержание в нем компонентов постоянное (это одно из допущений модели). Тогда между содержаниями цинка x и кадмия y должна существовать пропорциональная зависимость y = bx (b – коэффициент пропорциональности). Прямая y = bx должна проходить через две точки графика – начало координат и центр тяжести точек, соответствующий средним содержаниям цинка и кадмия в пробах.
Графический анализ зависимости (линия 1 на рис.1.1) показывает, что данная прямая не соответствует расположению точек. Это говорит о том, что геологическая и математические модели не соответствуют действительности. Прямая линия должна проходить вдоль удлинения облака точек, но тогда это будет не пропорциональная, а линейная зависимость, выражаемая уравнением y = a + bх (a и b – коэффициенты). Линия уравнения не проходит через начало координат, а отсекает на оси ординат отрезок а, т.е. при нулевом содержании цинка и, следовательно, сфалерита содержание кадмия равно не нулю, а значению а. Геологическое объяснение данного факта состоит в том, что некоторая часть кадмия имеется в других минералах и нужно проверить их состав.
В данном случае математическое моделирование позволяет из двух моделей (пропорциональной и линейной) выбрать одну, более достоверную, и помогает более правильно объяснить наблюдаемую зависимость.7
8Пример 1.3. Известна плотность руды и содержание в ней полезного компонента. Необходимо построить математическую модель зависимости этих величин, что актуально для руд многих черных и цветных металлов.
|
|
|
Для упрощения модели с целью выделения ее главных особенностей примем, что руда состоит из двух минералов (рудного и нерудного), их массы m 1 и m 2, объемы V 1 и V 2, плотности ρ1 и ρ2, содержания в них компонента С 1 и С 2, причем положим ρ1 > ρ2 и C 1 > C 2. В качестве аргумента x будет служить содержание компонента в руде:
. (1.2)
В качестве функции y будет плотность руды:
. (1.3)
Требуется найти математическое выражение зависимости плотности y от содержания x.
Очевидно, что V 1 = m 1/ρ1 и V 2 = m 2/ρ2. Подставляя их в формулу (1.3), получим
. (1.4)
Из формулы (1.3) найдем величину m 1:
Подставим ее в выражение (1.4). После преобразований получим
Обозначим
|
|
, 
.
В результате имеем гиперболическую зависимость плотности руды у от содержания в ней компонента x (рис.1.2):
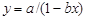, (1.5)
где a и b – постоянные коэффициенты.
Формула (1.5) представляет собою математическую модель зависимости.
Подобная зависимость часто используется на практике. Ее характер принципиально не изменится, если руда состоит из нескольких минералов, но появится разброс исходных данных около гиперболической зависимости, что вызвано колебаниями количественных соотношений минералов в руде и их состава.7
1.2.3. Основные виды математических моделей,
применяемых в геологии
Моделирование вообще и математическое моделирование в частности является эффективным средством изучения геологических систем, объектов и событий. Каждая модель служит некоторым их отражением и характеризует наиболее существенные особенности.
Модели можно разделить на материальные, аналоговые и символьные (рис.1.3).
Материальные модели представляют собой выполненные в определенном масштабе макеты геологических объектов. Например, существуют материальные модели кристаллических решеток минералов, модели идеальных кристаллов с различными наборами граней, морфологические модели рудных тел и др.
Аналоговые модели основаны на замене природных геологических процессов, явлений другими, воспроизводимыми в лаборатории, процессами, которые описываются одинаковыми математическими правилами и уравнениями. Например, движение подземных вод, процессы переноса в них вещества, явление диффузии и многие другие можно моделировать движением электрического тока в аналоговых устройствах.
Символьные модели, которые делятся на графические и математические, имеют особое значение при математическом моделировании. К графическим моделям относятся разнообразные геологические карты, разрезы, проекции, схемы и графики. Они позволяют наглядно изобразить геологические объекты и характеристики их свойств, а также дать интерпретацию многих операций математического моделирования.
Математические модели можно разделить на три группы. В первой группе анализируются характеристики в пределах однородных совокупностей свойств объектов вне связи их с пространственным размещением, это группа статистических моделей. Они бывают одномерные, двухмерные и многомерные.
Во второй группе учитываются пространственные координаты пунктов наблюдений, что позволяет изучать пространственные геологические поля. Модели делятся на детерминированные и вероятностные. В детерминированных моделях предполагается, что состояние системы однозначно определяется исходными или начальными данными и полностью предсказуемо в пространстве. Вероятностные модели характеризуются тем, что состояние системы и прогнозные значения свойств геологических объектов неоднозначно зависят от начальных или исходных данных и могут быть предсказаны с какой-то вероятностью в определенном диапазоне значений.
Третья группа охватывает случайные процессы, в которых учитывается фактор времени.
В настоящей книге будут рассмотрены модели первой и второй групп. Третья группа выходит за рамки дисциплины.
ОДНОМЕРНАЯ
СТАТИСТИЧЕСКАЯ МОДЕЛЬ
И ЕЕ ПРИМЕНЕНИЕ В ГЕОЛОГИИ
Глава
|
|
|
