Главная | Обратная связь | Поможем написать вашу работу! Архитектура Биология География Искусство История Информатика Маркетинг Математика Медицина Менеджмент Охрана труда Политика Правоотношение Разное Социология Строительство Физика Философия Финансы Химия Экология Экономика Электроника Расчет параболической зависимости, аппроксимирующей изменение мощности рудного тела   № п/п Исходные данные, м Произведения xi уi 1 2 0,7 4 8 16 1,4 2,8 0,49 2 6 1,3 25 125 625 6,5 32,5 1,69 3 7 2,6 49 343 2401 18,2 127,4 6,76 4 9 2,8 81 729 6561 25,2 226,8 7,84 5 12 2,0 144 1728 20738 24,0 288,0 4,00 6 14 1,8 196 2744 38416 25,2 352,8 3,24 7 16 1,0 256 4096 65536 16,0 256,0 1,00 8 19 0,4 381 6859 130321 7,6 144,4 0,16                                     Сумма 84 12,6 1116 18632 204612 124,1 1430,7 25,18 Среднее 10,5 1,575 139,5 2079 33076 15,51 178,8 3,148                     Сравнение фактических yi и теоретических у т мощностей, рассчитанных по уравнению параболы, свидетельствует об удовлетворительном их совпадении (табл.3.3). Расхождения d между фактическими и теоретическими значениями позволяют найти дисперсию случайных отклонений 0,104.   Таблица 3.3 Сравнение фактической и расчетной (теоретической) мощности   № п/п Исходные данные, м Расчетные величины xi уi y т, м d i 1 2 0,7 0,7 0,0 0,00 2 6 1,3 1,7 –0,4 0,16 3 7 2,6 2,2 0,4 0,16 4 9 2,8 2,4 0,4 0,16 5 12 2,0 2,3 –0,3 0,09 6 14 1,8 1,9 –0,1 0,01 7 16 1,0 1,4 –0,4 0,16 8 19 0,4 0,1 0,3 0,0,9                         Сумма 84 12,6 12,7 – 0,83 Среднее 10,5 1,575 1,6 – 0,104                 По формуле перехода от начальных моментов к центральным (2.14) найдем m 40 = 33076; m 30 = 2079; m 20 = 139,5; m 10 = 10,5; m 21 = 178,8; m 11 = 15,51; m 01 = 1,575; m 02 = 3,148; n = 8. Далее вычислим дисперсию исходных значений = 3,148 – 1,5752 = 0,667, откуда получим дисперсию, учтенную параболической зависимостью 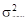= 0,667 – 0,104 = 0,563, и по формуле (3.26) определим корреляционное отношение: Корреляционное отношение близко к единице, следовательно, параболическая зависимость хорошо аппроксимирует эмпирические данные.7 3.1.7. Выбор порядка полинома при аппроксимации нелинейной зависимости Многие нелинейные зависимости могут быть аппроксимированы полиномом: ,                   (3.30) где m – порядок полинома; а 0, а 1, а 2, …, аm – коэффициенты полинома. Задача вычислений состоит в определении коэффициентов полинома с использованием метода наименьших квадратов. Чем выше порядок полинома, тем сложнее график, но при этом усиливается влияние случайных колебаний свойства, что отрицательно сказывается на надежности аппроксимации. Поэтому существует некоторый оптимальный порядок полинома, который наилучшим образом отражает исследуемую зависимость. Критерием выбора наилучшего порядка полинома, как и любой другой аппроксимирующей функции, является дисперсия  случайных отклонений фактических значений от теоретических с учетом степеней свободы k, .                                 (3.31) Таблица 3.4 Дисперсии отклонений n k 0 1 0,08346 0,9527 1 2 0,07835 0,1044 2 3 0,01745 0,0279 3 4 0,01569 0,0314 4 5 0,01039 0,0277 5 6 0,00949 0,0380

Количество степеней свободы k равно количеству постоянных коэффициентов в аппроксимирующей функции, в которой n – число наблюдений. Так, в квадратной параболе (3.27) три постоянных коэффициента, в параболе пятого порядка шесть коэффициентов, в синусоиде три коэффициента и т.д. При исследовании полинома повышают его порядок, начиная с m = 0, и анализируют дисперсию отклонений с учетом использованных степеней свободы k = m + 1. Как только остаточная дисперсия отклонений достигнет минимума, оптимальный порядок полинома получен, дальнейшее его повышение приведет к увеличению данной дисперсии. Для условий примера 3.3 наилучшая функция, аппроксимирующая исходные данные, – это полином четвертой степени (n = 4), что подтверждается данными табл.3.4.

3.1.8. Приведение нелинейных зависимостей

к линейному виду

Система уравнений (3.28), возникающая в результате применения метода наименьших квадратов к нелинейным зависимостям, лишь в редких случаях может быть решена алгебраическим путем. Простое решение системы возникает в случае полиномиальной зависимости. Система уравнений (3.28) для полиномов всегда является линейной. Поэтому по возможности стараются привести сложные для расчета зависимости к линейному или полиномиальному виду.

Например, показательная функция у = а е ^bx может быть приведена к линейному виду путем логарифмирования ln y = ln a + bx и замены переменной z = ln y,что приведет к линейному уравнению регрессии z = ln a + bx. Здесь неизвестными являются коэффициенты ln a и b. Существенно то, что отклонения d рассчитываются не от исходных значений у, а от их логарифмов, что не одно и то же.

Аналогично приводится к линейной логарифмическая функция y = a + b ln x путем замены переменной z = ln x, что дает уравнение y = a + bz.

Гиперболическая функция y = a /(1 + bx) приводится к общему знаменателю у + bxy = a, а потом делается замена z = xy. Получим линейную зависимость у + bz = a,обработка которой позволяет найти коэффициенты a и b. Подобные примеры можно продолжить и далее.