Главная | Обратная связь | Поможем написать вашу работу!

Пример выявления аномальных значений

Номер пробы n	Значения х	Квантиль t	Номер пробы n	Значения х	Квантиль t
1	0,06	-2,07	14	0,49	0,05
2	0,15	-1,57	15	0,50	0,15
3	0,21	-1,30	16	0,52	0,24
4	0,25	-1,10	17	0,53	0,34
5	0,28	-0,94	18	0,57	0,45
6	0,29	-0,80	19	0,60	0,56
7	0,32	-0,67	20	0,64	0,67
8	0,35	-0,56	21	0,67	0,80
9	0,38	-0,45	22	0,73	0,94
10	0,39	-0,34	23	0,75	1,10
11	0,42	-0,24	24	0,80	130
12	0,45	-0,15	25	1,14	1,57
13	0,47	-0,05	26	1,19	2,07

Вначале найдем среднее и дисперсию из всех 26 значений: = 0,502; s² = 0,06478; s = 0,2545. Далее вычислим среднее и дисперсию из 24 значений, исключив максимальные значения. Получим смещенные оценки 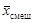= 0,451; = 0,03577; s = 0,1891. Вычислим нормированные значения исключенных значений: t ₂₅ = (1,14 – 0,451)/0,1891 = 3,64; t ₂₆ = (1,19 – 0,451)/0,1891 = 3,91. Поскольку нормированные значения t ₂₅ > 3 и t ₂₆ > 3, по правилу «трех сигм» оба исключенных значения являются аномальными. Однако полученный вывод является некорректным, так как он построен на смещенных оценках.

Оценим размер смещения, обусловленный исключением двух максимальных значений. Имеем p = 1 – n / N = 0,923. Вероятности p соответствует квантиль t = F ^–1(p) = 1,426. По формуле (2.25) найдем f (t) = 0,1443, по формуле (2.51) определим нормированное смещение у = 26/24×0,1443 = 0,1563. Из формулы (2.50) следует (1 – ty – t ²) = 0,03577/(1 – 1,426×0,1563 – 0,1563²) = = 0,04752; s = 0,218. Из формулы (2.49) получаем = х _смещ + + s _у = 0,451 + 0,218×0,1563 = 0,485. Полученные оценки приведены в табл.2.16.

Таблица 2.16

Результат вычисления истинных характеристик

Параметр	Исходная совокупность с учетом аномальных значений	Смещенные характеристики после исключения аномальных значений	Несмещенные «истинные» характеристики
Среднее значение	0,502	0,451	0,485
Дисперсия	0,06478	0,03577	0,4752
Среднеквадратичное отклонение	0,2545	0,1891	0,2180

По формуле (2.52) найдем смещенный критерий:

t _смещ = (3 + 0,1563)/ .

Отсюда следует, что, вместо t = 3 для проверки аномальности значений нужно пользоваться t _смещ = 3,638, что довольно существенно. Но и с учетом смещенного критерия исключенные значения являются аномальными.7

Поскольку смещение критерия t _смещ зависит только от отношения n / N, на основе формул (2.51) и (2.52) могут быть составлены таблицы t _смещ для различных значений t. Для примера приведена табл.2.17, соответствующая t = 3, т.е. правилу «трех сигм».

Аномальные значения можно выявить и на графике пробит-функции (рис.2.15), построенном по данным табл.2.15 по методике, описанной в подразделе 2.3.2. Большинство точек укладывается в одну линию, но две точки заметно отклоняются от нее, что свидетельствует об аномальности соответствующих им значений.

Таблица 2.17

Значения смещенного критерия t_с _мещ при заданном t = 3

n / N	0	1	2	3	4	5	6	7	8	9
0,00	3,000	3,019	3,034	3,048	3,061	3,073	3,085	3,096	3,107	3,117
0,01	3,128	3,138	3,148	3,157	3,167	3,176	3,186	3,195	3,204	3,213
0,02	3,221	3,230	3,239	3,247	2,256	3,264	3,272	3,280	3,289	3,297
0,03	3,305	3,313	3,320	3,328	3,336	3,344	3,351	3,359	3,367	3,374
0,04	3,382	3,389	3,397	3,404	3,411	3,419	3,426	3,433	3,440	3,448
0,05	3,455	3,462	3,469	3,476	3,483	3,490	3,497	3,504	3,511	3,518
0,06	3,525	3,532	3,538	3,545	3,552	3,559	3,566	3,572	3,579	3,586
0,07	3,592	3,599	3,606	3,612	3,619	3,626	3,632	3,639	3,645	3,652
0,08	3,658	3,665	3,671	3,678	3,684	3,691	3,697	3,704	3,710	3,717
0,09	3,723	3,729	3,736	3,742	3,748	3,755	3,761	3,767	3,774	3,780
0,10	3,786	3,793	3,799	3,805	3,811	3,818	3,824	3,830	3,836	3,842
0,11	3,849	3,855	3,861	3,867	3,873	3,879	3,886	3,892	3,898	3,904
0,12	3,910	3,916	3,922	3,928	3,935	3,941	3,947	3,953	3,959	3,965
0,13	3,971	3,977	3,983	3,989	3,995	4,001	4,007	4,013	4,019	4,025
0,14	4,031	4,037	4,043	4,049	4,055	4,061	4,067	4,073	4,079	4,085
0,15	4,091	4,097	4,103	4,109	4,115	4,121	4,127	4,133	4,139	4,145
0,16	4,151	4,157	4,163	4,169	4,175	4,181	4,187	4,193	4,198	4,204
0,17	4,210	4,216	4,222	4,228	4,234	4,240	4,246	4,252	4,258	4,264
0,18	4,269	4,275	4,281	4,287	4,293	4,299	4,305	4,311	4,317	4,323
0,19	4,328	4,334	4,340	4,346	4,352	4,358	4,364	4,370	4,376	4,381
0,20	4,387	4,393	4,399	4,405	4,411	4,417	4,423	4,429	4,434	4,440

Еще один способ выявления аномальных значений основан на применении критерия Титьена – Мура [14]. Если из нормально распределенной совокупности, содержащей N значений, исключить n максимальных или минимальных значений, то дисперсия уменьшится, и по степени ее уменьшения можно судить об аномальности исключенных значений. Вначале вычисляется величина

(2.53)

где – дисперсия исходной совокупности; – дисперсия после исключения n предполагаемых аномальных значений.

Если значение L окажется меньше критерия L _доп при заданной вероятности a, то исключенные значения являются аномальными. Для примера приведена табл.2.18 с вероятностью a = 0,05 [14].

Таблица 2.18

Критерий Титьена – Мура при a = 0,05

N	Количество исключенных значений n
N	1	2	3	4	5	6	7	8	9	10
3	0,003
4	0,051	0,001
5	0,125	0,018
6	0,203	0,055	0,010
7	0,273	0,106	0,032
8	0,326	0,146	0,064	0,022
9	0,372	0,194	0,099	0,045
10	0,418	0,233	0,129	0,070	0,034
11	0,454	0,270	0,162	0,098	0,054
12	0,489	0,305	0,196	0,125	0,076	0,042
13	0,517	0,337	0,224	0,150	0,098	0,060
14	0,540	0,363	0,250	0,174	0,122	0,079	0,050
15	0,556	0,387	0,276	0,197	0,140	0,097	0,066
16	0,575	0,410	0,300	0,219	0,159	0,115	0,082	0,055
17	0,594	0,427	0,322	0,240	0,181	0,136	0,100	0,072
18	0,608	0,447	0,337	0,259	0,200	0,154	0,116	0,086	0,062
19	0,624	0,462	0,354	0,277	0,209	0,168	0,130	0,099	0,074
20	0,639	0,484	0,377	0,299	0,238	0,188	0,150	0,115	0,088	0,066
25	0,696	0,550	0,450	0,374	0,312	0,262	0,222	0,184	0,154	0,126
Окончание табл.2.18
N	Количество исключенных значений n
N	1	2	3	4	5	6	7	8	9	10
30	0,730	0,599	0,506	0,434	0,376	0,327	0,283	0,245	0,212	0,183
35	0,762	0,642	0,554	0,482	0,424	0,376	0,334	0,297	0,264	0,235
40	0,784	0,672	0,588	0,523	0,468	0,421	0,378	0,342	0,310	0,280
45	0,802	0,696	0,618	0,556	0,502	0,456	0,417	0,382	0,350	0,320
50	0,820	0,722	0,646	0,588	0,535	0,490	0,450	0,414	0,383	0,355

Примерим критерий Титьена – Мура к данным табл.2.15. Дисперсия исходной совокупности = 0,06478; дисперсия после исключения двух значений = 0,03577. Следовательно,

Из табл.2.18 интерполяцией находим критерий L _доп = 0,560. Так как L < L _доп, то исключенные значения являются аномальными.

На графике пробит-функции при большом количестве данных можно выявить и другие особенности поведения случайной величины. На рис.2.16 показаны фактические данные по содержанию меди на колчеданном месторождении. Стрелками выделены две точки – нижняя и верхняя. В верхней точке проходит граница аномальных проб (более 16 %), в нижней точке – естественная природная граница кондиционных руд (около 0,5 %). Средняя часть графика близка к прямой линии, что соответствует нормальному закону распределения.

2.3.4. Выделение однородных совокупностей

Одна из сложных проблем при обработке статистических данных – это разделение неоднородной совокупности на однородные. Заключение о неоднородности совокупности лучше всего делать по гистограмме частот. Например, на рис.2.17 явно выделяются два максимума частот, соответствующие двум однородным совокупностям. Одна совокупность имеет моду при 27 % содержания железа, другая – при 55 %. Геологическая причина появления двух совокупностей заключается в том, что бедные руды возникли путем замещения алюмосиликатных пород, а богатые – карбонатных пород.

Для статистического исследования рекомендуется разделить данные опробования на две однородные совокупности. Это можно сделать двумя способами: 1) раздельным изучением руд, образованных по алюмосиликатным и карбонатным породам (геологический способ изучения); 2) аналитическим способом, что требует применения сложных расчетов при условии, что задан или известен закон распределения каждой совокупности

Возможна и обратная ситуация: наличие неоднородной совокупности на гистограмме позволяет сделать определенные геологические выводы.

Так, на рис.2.18 показано распределение стронция в апатите в логарифмическом масштабе. На гистограмме выделяются три однородные совокупности. Первая совокупность соответствует содержанию SrO 0,01-0,05 %, вторая 0,05-1 %, третья 1-13 %. Следовательно, имеется три разновидности апатита с различным содержанием стронция. Анализ адресов проб показывает, что они относятся к различным типам месторождений и горных пород. Наиболее чистыми по содержанию стронция являются апатиты из гранитоидов, ультрабазитов и метаморфических пород. Средние по содержанию стронция – это апатиты скарновых месторождений и некоторых массивов щелочных пород. Наиболее высокие содержания стронция наблюдаются в апатитах Хибинской группы месторождений.

Однородные совокупности, входящие в смешанную совокупность, различаются средними значениями и дисперсиями Важным показателем, определяющим возможность аналитического разделения смешанных совокупностей при условии нормального их распределения, является раздвиг распределений:

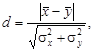(2.54)

который по смыслу близок к критерию t. Чем больше раздвиг, тем легче разделить неоднородную совокупность на однородные и определить их характеристики. Можно выделить несколько вариантов разделения:

1. Раздвиг очень большой (d > 4), гистограмма распадается на две самостоятельные гистограммы, не перекрывающие друг друга (рис.2.19, а).

2. Раздвиг большой (d = 2¸4), гистограмма является бимодальной, совокупности частично перекрываются (рис.2.19, б и рис.2.17). Однородные совокупности можно разделить либо аналитическим путем, либо используя геологическую информацию.

3. Раздвиг малый (d = 0,7¸2), гистограмма одномодальная, но имеет искаженную асимметричную форму (рис.2.19, в). Аналитическое разделение ее на однородные совокупности все же возможно.

4. Раздвиг незначительный (d < 0,7), гистограмма одномодальная (рис.2.19, г), разделить ее на однородные совокупности практически невозможно.

Таким образом, перед статистической обработкой данных необходимо стараться разделить неоднородную совокупность на однородные и удалить из расчетов аномальные значения.

ДВУХМЕРНАЯ

СТАТИСТИЧЕСКАЯ МОДЕЛЬ

И ЕЕ ПРИМЕНЕНИЕ В ГЕОЛОГИИ

Глава

Предыдущая 2 3 4 5 6 7 8910 11 12 13 14 15 16 17 Следующая

Воспользуйтесь поиском по сайту: