 |
Одномерной статистической модели
|
|
|
|
2.3.1. Точечная оценка погрешности среднего значения
Среднее значение 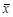 из n независимых значений случайной величины х также является случайной величиной. Если случайная величина х имеет дисперсию s2, то среднее значение
из n независимых значений случайной величины х также является случайной величиной. Если случайная величина х имеет дисперсию s2, то среднее значение  , как показано в подразделе 2.1.2, имеет дисперсию d2 в n раз меньше:
, как показано в подразделе 2.1.2, имеет дисперсию d2 в n раз меньше:
d2 = s2/ n или  . (2.46)
. (2.46)
Величину d можно рассматривать как абсолютную среднеквадратичную случайную погрешность среднего значения 
Если разделить обе части равенства (2.46) на среднее значение 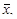 то получим относительную погрешность
то получим относительную погрешность
 , (2.47)
, (2.47)
где V – коэффициент вариации. Относительная погрешность может быть выражена в долях единицы или в процентах.
Формулы (2.46) и (2.47) играют большую роль: они показывают, что погрешность среднего значения прямо пропорциональна изменчивости случайной величины и обратно пропорциональна корню квадратному из числа измерений. Это позволяет решать две задачи: 1) оценивать абсолютную d или относительную t погрешность среднего значения при известном числе наблюдений n; 2) находить необходимое число измерений n для достижения заданной погрешности среднего значения.
8 Пример 2.6. В результате анализа 16 проб гранита рассчитано среднее содержание кремнезема 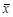 = 70,35 % и среднеквадратичное отклонение s2 = 3,20 %. Определить, чему равна среднеквадратичная погрешность среднего содержания и сколько дополнительно нужно взять проб, чтобы снизить относительную погрешность до 1 %.
= 70,35 % и среднеквадратичное отклонение s2 = 3,20 %. Определить, чему равна среднеквадратичная погрешность среднего содержания и сколько дополнительно нужно взять проб, чтобы снизить относительную погрешность до 1 %.
Абсолютная среднеквадратичная случайная погрешность d = = 3,20/  = 0,80 %; относительная случайная погрешность t = = 0,80/70,35 = 1,14 %.
= 0,80 %; относительная случайная погрешность t = = 0,80/70,35 = 1,14 %.
Продолжим задачу. Если t = 1 % = 0,01, то из формулы (2.47) получим  Из формулы (2.46) имеем n = s2/d2 = 3,202/0,702 = 21. Следовательно, дополнительно нужно взять и проанализировать 21 – 16 = 5 проб.7
Из формулы (2.46) имеем n = s2/d2 = 3,202/0,702 = 21. Следовательно, дополнительно нужно взять и проанализировать 21 – 16 = 5 проб.7
|
|
|
2.3.2. Интервальная оценка математического ожидания случайной величины
Обычно среднее значение случайной величины  находят по выборке из генеральной совокупности. Математическое ожидание случайной величины в генеральной совокупности М (х) обычно неизвестно. Его можно приближенно оценить с помощью выборочного среднего значения
находят по выборке из генеральной совокупности. Математическое ожидание случайной величины в генеральной совокупности М (х) обычно неизвестно. Его можно приближенно оценить с помощью выборочного среднего значения  которое является случайной величиной и имеет дисперсию d2. Чаще всего с достаточным основанием предполагается, что случайная величина
которое является случайной величиной и имеет дисперсию d2. Чаще всего с достаточным основанием предполагается, что случайная величина  как представляющая собою сумму многих случайных величин, имеет распределение, близкое к нормальному. Размах значений нормально распределенной величины составляет приближенно ±3d (ширина кривой нормального распределения на рис.2.7). Где-то в этом интервале и заключено математическое ожидание М (х). Наиболее вероятно, что оно совпадает со средним значением
как представляющая собою сумму многих случайных величин, имеет распределение, близкое к нормальному. Размах значений нормально распределенной величины составляет приближенно ±3d (ширина кривой нормального распределения на рис.2.7). Где-то в этом интервале и заключено математическое ожидание М (х). Наиболее вероятно, что оно совпадает со средним значением  которое является точечной оценкой математического ожидания. Менее вероятно, что математическое ожидание смещено в ту или иную сторону от среднего значения. Интервал возможных значений математического ожидания зависит от вероятности q = Ф(t) и выражается через коэффициент вероятности t соотношением
которое является точечной оценкой математического ожидания. Менее вероятно, что математическое ожидание смещено в ту или иную сторону от среднего значения. Интервал возможных значений математического ожидания зависит от вероятности q = Ф(t) и выражается через коэффициент вероятности t соотношением
 – t d < М (х) <
– t d < М (х) <  + t d. (2.48)
+ t d. (2.48)
Данный интервал называется доверительным интервалом или интервальной оценкой математического ожидания. Каждому значению вероятности q соответствует определенный коэффициент вероятности t (табл.2.6 и 2.7) и размер доверительного интервала:
| Вероятность q = Ф(t) | Коэффициент вероятности t | Доверительный интервал |
| 0,683 | 1 | 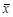 – d < М (х) < – d < М (х) <  + d + d
|
| 0,954 | 2 |  – 2d < М (х) < – 2d < М (х) <  + 2d + 2d
|
| 0,997 | 3 |  – 3d < М (х) < – 3d < М (х) <  + 3d + 3d
|
Используя данные примера 2.6, в котором известно среднее содержание кремнезема в граните  = 70,35 %, и d = 0,80 %, получаем доверительные интервалы:
= 70,35 %, и d = 0,80 %, получаем доверительные интервалы:
| Вероятность q | Доверительный интервал |
| 0,683 | 69,65 < М (х) < 71,15 |
| 0,954 | 68,75 < М (х) < 71,95 |
| 0,997 | 67,95 < М (х) < 72,75 |
|
|
|
Какую из вероятностей q принять за основу, нельзя решить математическим путем, так как ответ лежит в области принятия решений и должен опираться на какое-то логическое или экономическое обоснование. Практически в менее ответственных случаях принимают t = 2 и q = 0,954, в более ответственных случаях t = 3 и q = 0,997. При наличии достаточного обоснования могут приниматься и дробные значения t.
Если среднее значение  или другая оцениваемая величина подчиняются не нормальному, а другому закону распределения, то, естественно, вероятность q будет иная.
или другая оцениваемая величина подчиняются не нормальному, а другому закону распределения, то, естественно, вероятность q будет иная.
2.3.3. Выделение аномальных значений
Статистические характеристики и получаемые на их основе выводы имеют смысл лишь для однородных совокупностей. При объединении двух и более однородных совокупностей с различными статистическими характеристиками расчеты по объединенной совокупности обычно не имеют смысла. Искажение статистических характеристик происходит и в том случае, когда в однородную совокупность попадают единичные значения, значительно отличающиеся от среднего, называемые аномальными или ураганными. Поэтому актуальной является задача о разделении неоднородной совокупности на однородные, о выделении из неоднородных совокупностей аномальных значений. Данная задача имеет несколько способов решения при условии, что известен или задан закон распределения случайной величины.
Распространенный способ выделения аномальных значений называется правилом «трех сигм» и основан на том, что случайная величина при нормальном законе распределения практически полностью (на 99,7 %) заключена в пределах от 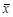 – 3s до
– 3s до  + 3s (см. рис.2.7). Если значение случайной величины отличается от среднего значения
+ 3s (см. рис.2.7). Если значение случайной величины отличается от среднего значения  больше чем на 3s, то оно является аномальным. Естественно, что испытуемое значение не должно участвовать в расчете среднего значения и среднеквадратичного отклонения. Для удобства расчетов можно нормировать случайную величину по формуле (2.24). Тогда правило «трех сигм» преобразуется: если нормированное значение | t | > 3, то оно является аномальным.
больше чем на 3s, то оно является аномальным. Естественно, что испытуемое значение не должно участвовать в расчете среднего значения и среднеквадратичного отклонения. Для удобства расчетов можно нормировать случайную величину по формуле (2.24). Тогда правило «трех сигм» преобразуется: если нормированное значение | t | > 3, то оно является аномальным.
8 Пример 2.7. Средняя зольность угля  = 6,5 %, среднеквадратичное отклонение s = 2,1 %. Определить, не является ли аномальной проба угля с зольностью 15 %.
= 6,5 %, среднеквадратичное отклонение s = 2,1 %. Определить, не является ли аномальной проба угля с зольностью 15 %.
|
|
|
Найдем нормированное значение t = (15 – 6,5)/2,1 = 4,05. Поскольку t > 3, проба является аномальной и относится к другой совокупности.
На основе приведенных данных можно определить, какие вообще значения зольности являются аномальными. Так как 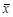 – 3s = = 6,5 – 3×2,1 = 0,2 %;
– 3s = = 6,5 – 3×2,1 = 0,2 %;  – 3s = 6,5 + 3×2,1 = 12,8 %, то аномальными являются значения зольности менее 0,2 и более 12,8 %.7
– 3s = 6,5 + 3×2,1 = 12,8 %, то аномальными являются значения зольности менее 0,2 и более 12,8 %.7
Если распределение случайной величины логнормальное, то правило «трех сигм» применяется к логарифмам значений, что используется при геохимическом методе поисков месторождений для выделения геохимических аномалий.
8 Пример 2.8. Среднее (фоновое) содержание меди  = = 0,018, дисперсия натуральных логарифмов
= = 0,018, дисперсия натуральных логарифмов 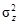 = 0,22. Определить, какие содержания меди надо считать аномальными.
= 0,22. Определить, какие содержания меди надо считать аномальными.
Используя формулы подраздела 2.2.3, найдем σ z =  = = 0,47;
= = 0,47;  = ln
= ln  –
– 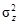 /2 = ln0,018 – 0,22/2 = –4,13. Нижний предел логарифмов z 1 =
/2 = ln0,018 – 0,22/2 = –4,13. Нижний предел логарифмов z 1 =  – 3s z = –4,13 – 3×0,47 = –5,54. Верхний предел логарифмов z 2 = ln
– 3s z = –4,13 – 3×0,47 = –5,54. Верхний предел логарифмов z 2 = ln  +
+ 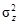 /2 = –4,13 + 3×0,47 = –2,72. Так как z = ln х, то х = e z и получаем нижний предел содержаний х 1 = е–5,54 = 0,004 %, верхний предел х 2 = е–2,72 = 0,066 %. Следовательно, аномальными являются содержания меди менее 0,004 и более 0,066 %. На практике нижним пределом обычно пренебрегают, полагая его равным нулю.7
/2 = –4,13 + 3×0,47 = –2,72. Так как z = ln х, то х = e z и получаем нижний предел содержаний х 1 = е–5,54 = 0,004 %, верхний предел х 2 = е–2,72 = 0,066 %. Следовательно, аномальными являются содержания меди менее 0,004 и более 0,066 %. На практике нижним пределом обычно пренебрегают, полагая его равным нулю.7
Наряду с правилом «трех сигм» существуют и другие правила выявления аномальных значений. Более общее правило состоит в том, что задается либо вероятность q, либо соответствующая ей предельная величина критерия t. Если нормированное значение превышает предельное значение t, то значение случайной величины является аномальным.
Следует учесть, что при исключении аномальных значений происходит искажение (смещение) статистических характеристик оставшейся совокупности. Так, если из нормально распределенной совокупности исключить одно или несколько максимальных значений, то уменьшатся среднее значение и дисперсия – возникает усеченное нормальной распределение. Это обстоятельство рекомендуется учитывать при выделении аномальных значений.
|
|
|
Обозначим смещенные характеристики усеченного распределения: среднее значение 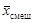 и дисперсия
и дисперсия  , тогда их связь с несмещенными характеристиками выражается формулами
, тогда их связь с несмещенными характеристиками выражается формулами
 (2.49)
(2.49)
 =
=  (1 – ty – y 2); (2.50)
(1 – ty – y 2); (2.50)
 , (2.51)
, (2.51)
где у – нормированное смещение среднего; n – число исключенных значений; N – общее число значений случайной величины; f (t) – функция плотности вероятности (2.25); t – квантиль нормального распределения, соответствующая вероятности p = 1 – n / N, т.е. t = F –1(1 – n / N).
Поскольку статистические характеристики изменяются, происходит и смещение критерия t:
 (2.52)
(2.52)
Из приведенных формул следует, что величины t, f (t), y, t смещ зависят только от отношения n / N.
8 Пример 2.9. Необходимо проверить аномальность максимальных значений табл.2.15.
Таблица 2.15
|
|
|


