 |
Расчет случайной погрешности химического анализа
|
|
|
|
| Номер пробы ni | Содержание меди, % | Разность xi – yi | Квадрат разности (xi – yi)2 | |||
| Основные пробы xi | Контрольные пробы yi | |||||
| 1 | 2,74 | 2,70 | 0,04 | 0,0016 | ||
| 2 | 2,14 | 2,44 | –0,30 | 0,0900 | ||
| 3 | 2,33 | 2,19 | 0,14 | 0,0196 | ||
| 4 | 2,57 | 2,54 | 0,03 | 0,0009 | ||
| 5 | 2,16 | 2,24 | –0,08 | 0,0064 | ||
| 6 | 1,27 | 1,21 | 0,06 | 0,0036 | ||
| 7 | 1,00 | 1,23 | –0,23 | 0,0529 | ||
| 8 | 0,95 | 0,59 | 0,36 | 0,1296 | ||
| 9 | 1,72 | 1,28 | 0,44 | 0,1936 | ||
| 10 | 2,06 | 1,76 | 0,30 | 0,0090 | ||
| 11 | 1,06 | 1,43 | –0,37 | 0,1369 | ||
| 12 | 1,83 | 1,83 | 0,00 | 0,0000 | ||
| 13 | 2,13 | 1,81 | 0,32 | 0,1024 | ||
| 14 | 3,04 | 3,16 | –0,12 | 0,0144 | ||
| 15 | 1,52 | 1,34 | 0,18 | 0,0324 | ||
| 16 | 1,48 | 1,63 | –0,15 | 0,0225 | ||
| 17 | 0,78 | 0,82 | –0,04 | 0,0016 | ||
| 18 | 0,92 | 0,60 | 0,32 | 0,1024 | ||
| 19 | 2,17 | 2,62 | –0,45 | 0,2025 | ||
| 20 | 2,96 | 2,56 | 0,40 | 0,1600 | ||
| 21 | 1,45 | 1,79 | –0,34 | 0,1156 | ||
| 22 | 1,82 | 1,83 | –0,01 | 0,0001 | ||
| 23 | 2,51 | 2,29 | 0,22 | 0,0484 | ||
| 24 | 1,70 | 2,18 | –0,48 | 0,2304 | ||
|
| ||||||
|
| ||||||
| Сумма | 44,31 | 44,07 | 0,24 | 1,7578 | ||
| Среднее | 1,85 | 1,84 | – | – | ||
| Абсолютная случайная погрешность 0,191 | ||||||
| Относительная случайная погрешность 10,4 % | ||||||
|
|
Для выявления случайной погрешности рекомендуется проводить графический анализ (рис.3.9) – облако точек должно группироваться около биссектрисы угла хОy. Если какие-то точки сильно удалены от биссектрисы, то соответствующие им пробы классифицируют как промахи, они должны быть исключены из расчета.
3.2.4. Внешний контроль химических анализов
В геологической практике принято регулярно оценивать систематическую погрешность измерений. Наиболее часто определяется погрешность опробования или ее составная часть – погрешность химического анализа, для чего выполняется внешний контроль анализов. Главное требование при изучении систематических погрешностей (или систематических расхождений) – неравноточность основных и контрольных измерений. Для выполнения этого условия основные пробы посылают в одну лабораторию, а контрольные – в другую, где анализ выполняют, как правило, по более совершенной методике. Сравнение анализов основных и контрольных проб позволяет оценить систематическую погрешность анализов.
|
|
|
Обозначим xi – данные основных проб, yi – данные контрольных проб. Для выявления систематической погрешности применяются графический и аналитический методы. При графическом анализе проверяется расположение точек графика. При отсутствии систематической погрешности они должны располагаться вдоль биссектрисы у = х. Из-за наличия неизбежных случайных погрешностей точки рассеиваются около биссектрисы, образуя облако. Если  облако точек смещено относительно биссектрисы, то можно предполагать, что в основных (а иногда и в контрольных) пробах имеется систематическая погрешность (рис.3.10).
облако точек смещено относительно биссектрисы, то можно предполагать, что в основных (а иногда и в контрольных) пробах имеется систематическая погрешность (рис.3.10).
|
|
Для более точного доказательства систематической погрешности применяются аналитические методы. Наиболее распространенный прием основан на сравнении средних значений  и
и 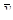 с помощью критерия
с помощью критерия
 при
при  , (3.34)
, (3.34)
где n – число контрольных проб.
Если критерий t окажется больше допустимого t доп, то систематическая погрешность доказана. Допустимое значение критерия t доп находят на основе распределения Стьюдента при вероятности b = 0,05 и числе степеней свободы k = n – 1 (см. табл.2.10). При увеличении числа контрольных проб распределение Стьюдента приближается к нормальному и в пределе t доп = 1,960.
Метод выявления систематической погрешности, основанный на сравнении средних значений  и
и 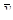 , обладает существенным недостатком: равенство средних еще не гарантирует наличия систематических расхождений при низких и высоких содержаниях. Последние могут быть направлены в разные стороны и в среднем компенсируют друг друга.
, обладает существенным недостатком: равенство средних еще не гарантирует наличия систематических расхождений при низких и высоких содержаниях. Последние могут быть направлены в разные стороны и в среднем компенсируют друг друга.
|
|
|
Более рациональной является методика, основанная на оценке коэффициентов уравнения регрессии y = ax + b. При отсутствии систематической погрешности должны выполняться условия а = 1 и b = 0. Поэтому вычисляют уравнение регрессии между содержаниями в основных и контрольных пробах и находят соответственно два критерия:
Таблица 3.6
|
|
|



