Главная | Обратная связь | Поможем написать вашу работу! Архитектура Биология География Искусство История Информатика Маркетинг Математика Медицина Менеджмент Охрана труда Политика Правоотношение Разное Социология Строительство Физика Философия Финансы Химия Экология Экономика Электроника Результаты распознавания объектов Номер испытуемого объекта Количество признаков объектов Вывод о принадлежности испытуемых объектов рудных безрудных 1 5 0 Рудный 2 0 6 Безрудный 3 1 3 "–"

Используя сведения по испытуемым объектам и данные табл.4.17, можно подсчитать, что для первого испытуемого объекта характерны признаки только рудных объектов, для второго – только безрудных, у третьего испытуемого объекта есть те и другие признаки, но больше «голосов» в пользу безрудных объектов (табл.4.18).7

Другой алгоритм распознавания основан на анализе образов рудных и безрудных объектов, которые в признаковом пространстве слагают два соответствующих облака, которые могут частично перекрывать друг друга. Принадлежность испытуемого объекта к образу рудных или безрудных объектов можно оценить по расстоянию точки испытуемого объекта от облаков. К какому облаку ближе точка, к тому образу и следует отнести испытуемый объект.

Существуют различные способы оценки расстояний между точкой и облаком. Можно рекомендовать следующий способ: вначале найти расстояния до всех точек облака, а потом взять среднее из них. Для оценки расстояния между точкой испытуемого объекта х _исп и точкой облака х_i применима формула

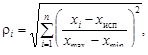                         (4.31)

где x _maxи x _min – максимальные и минимальные значения различных свойств i; x _max– x _min – размах свойств.

Далее вычислим среднее расстояние точки до облака:

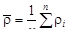.                                  (4.32)

8 Пример 4.9. Даны пять рудных, шесть безрудных и два испытуемых объекта, у которых изучены три свойства:

; ; .

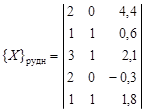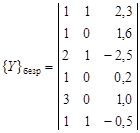Требуется определить принадлежность испытуемых объектов к рудным или к безрудным.

Вначале найдем максимальные и минимальные значения свойств:

; .

По формуле (4.31) определим расстояние точки первого испытуемого объекта от одной из точек облака рудных объектов:

.

Таким же способом найдем расстояние для всех остальных точек облаков и рассчитаем среднее расстояние до каждого облака по формуле (4.32). Для первого испытуемого объекта получим  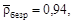следовательно, он ближе к рудным объектам. Второй испытуемый объект имеет  он ближе к безрудным.7

Следующая группа методов основана на разделении признакового пространства на области, в которых преобладают объекты одного типа. Чаще области выделяются путем проведения плоскостей (гиперплоскостей) между облаками рудных и безрудных объектов. Такой способ называется дискриминантным анализом.

Уравнение плоскости имеет вид

,                                (4.33)

где a_i – коэффициенты, определяющие ориентировку плоскости по отношению к осям координат признакового пространства и вычисляемые путем решения системы уравнений (4.29); b – коэффициент, влияющий на параллельное перемещение плоскости в пространстве.

Если подставить координаты x_i любой точки облака в уравнение (4.33), то получим дискриминант этой точки:

.                               (4.34)

По одну сторону от плоскости знак дискриминанта положительный, по другую – отрицательный. Следовательно, по знаку дискриминанта можно судить о том, в какую область пространства попадает точка испытуемого объекта, т.е. к какому образу следует отнести объект.

Если облака рудных и безрудных объектов разобщены между собой, то плоскость можно провести в любом месте между ними. Если облака частично перекрываются, то нужно провести разделяющую плоскость так, чтобы наименьшая часть точек попадала в чужую область, что достигается нахождением наилучшего значения коэффициента b. Подбор коэффициента b можно осуществлять вручную (а также и коэффициентов а_i), но можно вычислить его следующим способом. Вначале находят коэффициент p для каждой точки облаков:

.                                   (4.35)

Далее вычисляют средние значения и дисперсии значений р для рудных и безрудных объектов, т.е.  и  Обычно предполагают, что значения коэффициентов р подчиняются или близки к нормальному закону распределения, тогда определение коэффициентов b сводится к решению квадратного уравнения

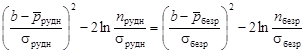.  (4.36)

8 Пример 4.10. Используя данные примера 4.7, необходимо найти уравнение плоскости, разделяющей образы рудных и безрудных объектов, и дискриминанты объектов.

Выпишем значения информативных свойств (второго и третьего):

Средние значения свойств:

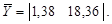
Матрица ковариации свойств: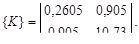

Составим систему уравнений (4.29):

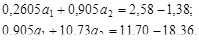
Решение системы дает коэффициенты  

Вычислим значения р для рудных и безрудных объектов по формуле (4.35):

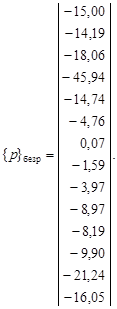
Средние значения  дисперсии 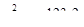 Подставив полученные значения в уравнение (4.36) и решая его, найдем один из корней b = 0,56, следовательно, уравнение плоскости (в данном случае – это прямая линия, рис.4.6) имеет вид

9,57 х ₁ – 1,427 х ₂ + 0,56 = 0,

а дискриминант выражается формулой

D = 9,57 х ₁ – 1,427 х ₂ + 0,56.

Значения дискриминанта отличаются от значений р лишь коэффициентом b = 0,56. Для рудных объектов значения дискриминанта, как правило, положительные, для безрудных – отрицательные. Только в трех случаях из 24 знак дискриминанта не отвечает принадлежности объектов, т.е. ошибка распознавания составляет 3/24 = 0,125 = = 12,5 %.7

Следует отметить, что на практике (например, при обогащении руд) может быть использована комбинация дискриминантного анализа с методом главных компонент (подраздел 4.2.2). Если на графике главных компонент рудные и безрудные объекты дают два различных облака, то между ними можно провести дискриминантную плоскость, как описано в данном подразделе (рис.4.7).

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ПРОСТРАНСТВЕННЫХ

ГЕОЛОГИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ

Глава

5.1. СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕ

В данной главе свойства будут изучены как функции координат пространства – пространственные переменные. В роли пространственных переменных могут выступать мощность пластообразных тел, абсолютные отметки кровли и почвы пласта, содержание компонентов в рудном теле и многие другие величины.

Пространство, в котором существует изучаемая величина, называется геологическим полем пространственной переменной. В каждой точке или области геологического поля с координатами x, у, z свойство принимает конкретное значение j(х, у, z). В общем случае в каждой точке или области геологического поля могут быть измерены несколько величин.

Значения пространственной переменной измеряют в пределах геологических объектов конечных размеров по какой-то сети в ограниченных областях геологического поля. В связи с этим рассмотримпараметры геометрии сети наблюдений и области измерений.

Геометрия сети наблюдений характеризуется формой, расположением и плотностью сети. Сеть бывает одномерная – вдоль линии, двухмерная – по площади и трехмерная – в объеме геологического тела. Измерения делят на непрерывные и дискретные (прерывистые). Для математической обработки непрерывные измерения обычно преобразуют в дискретные.

Наблюдения могут размещаться по равномерной, кратной или неравномерной сети. Равномерная сеть характеризуется постоянным шагом h – равным расстоянием между пунктами наблюдений. В двухмерной сети имеется два постоянных шага h ₁ и h ₂, которые образуют ячейку сети площадью s = h ₁ h ₂. Если h ₁ = h ₂, то сеть квадратная. Трехмерная сеть имеет три постоянных шага h ₁, h ₂, h ₃, образующих ячейку объемом v = h ₁ h ₂ h ₃. В реальных условиях не всегда удается соблюдать строго равномерную сеть наблюдений. Небольшими отклонениями от равномерной сети часто можно пренебречь. У кратной сети расстояния между пунктами наблюдений непостоянные, но кратные шагу h.

Плотность сети – количество наблюдений на единицу длины, площади или объема геологического объекта. Если сеть наблюдений отличается от равномерной, то можно говорить о средней плотности сети.

Обычно пространственная переменная предполагается непрерывной величиной, плавно меняющей свое значение в геологическом поле. Но возможны сравнительно резкие и даже скачкообразные изменения пространственной переменной, отражающие дискретность строения геологических объектов и позволяющие проводить внутри них геологические границы.

Геометрия области измерения характеризуется формой, размером и ориентировкой. Форма области может быть точечной, линейной, сферической, цилиндрической и пр. Во многих случаях формой области можно пренебречь, полагая ее точечной.

Размер области наблюдения влияет на некоторые характеристики. Например, при увеличении размера области уменьшается дисперсия величин. Размером области измерения также часто пренебрегают, считая измерения точечными, тем более что размеры области обычно на порядок ниже шага сети наблюдений.

При уменьшении размеров области некоторые измерения стремятся к предельному значению величины в данной точке, что характерно для непрерывных величин, например для мощности пластообразных геологических тел. В других случаях такой предел отсутствует из-за дискретности строения геологических объектов (например, руда состоит из зерен рудных и нерудных минералов). В этих случаях принято говорить о средних значениях пространственной переменной в некоторой малой области геологического поля.

Ориентировка области измерений имеет значение для анизотропных геологических тел, а их большинство. При различной ориентировке линейных или цилиндрических областей в анизотропной среде можно получить разные результаты. Обычно стараются линейные пробы располагать по направлению наибольшей изменчивости свойств, т.е. по мощности рудных тел или пластов горных пород.

Результаты измерений пространственных переменных сводят в матрицу, в которой присутствуют значения величины  j и координаты пунктов наблюдений (центров областей измерений) х, у, z:

.                  (5.1)

Напомним, что n – количество объектов, k – количество величин. В зависимости от количества учитываемых координат пространственные переменные и геологические поля делятся на одно-, двух- и трехмерные.

5.2. ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

И ГЕОЛОГИЧЕСКИХ ПОЛЕЙ

Математическое моделирование геологического поля ставит своей целью описание поведения пространственной переменной по имеющимся результатам наблюдений, а также прогнозирование ее значений в заданных точках или областях геологического поля. Попутно могут быть решены задачи оценки погрешности прогнозирования, рациональной плотности сети измерений и другие.

Реальные геологические поля пространственных переменных обладают большой сложностью. Математические модели геологических полей не позволяют дать их исчерпывающую характеристику, а отражают лишь наиболее существенные черты. Для каждого геологического поля можно построить много математических моделей, различающихся характером предположений о поведении величин в пространстве.

Математические модели геологических полей делятся на детерминированные и вероятностные. В детерминированных моделях предполагается, что пространственная переменная является неслучайной функцией координат и однозначно зависит от местоположения пунктов измерений. В тех пунктах, где проводились измерения, значения пространственной переменной принимают фактическими, а в промежутках между ними находят путем интерполяции. Способ интерполяции определяет вид математической модели. Среди детерминированных моделей можно выделить модели линейные, полиномиальные, обратных расстояний и сплайн-модели.

В вероятностных моделях предполагается, что значения пространственной переменной (в том числе и в пунктах измерений) содержат элементы случайности. Различают две группы математических моделей: случайные функции и геостатистические модели. В разных группах по-разному объясняется появление случайной составляющей.

Случайные функции основаны на предположении о том, что значения пространственной переменной j(х) испытывают случайные колебания δ(х) около неслучайной составляющей, называемой математическим ожиданием m (x):

j(х) = m (x) + d(х).                              (5.2)

В геологической литературе математическое ожидание называют также регулярной, координированной, закономерной составляющей или трендом. Математическое ожидание иногда делят на регулярную f (x) и периодическую w(х) составляющие:

m (x) = f (x) + w(х).                               (5.3)

Может быть несколько периодических составляющих, различающихся амплитудой и длиной волны.

Геостатистические модели содержат предположение о том, что случайный результат измерений вызван случайным расположением пунктов наблюдений. Любое перемещение сети наблюдений приводит к получению новых результатов, но при этом остается неизменным средний квадрат разности между результатами измерений в пунктах, отстоящих друг от друга на шаг h. Полусумма среднего квадрата разностей называется вариограммой γ(h)

.                   (5.4)

Геостатистические модели различаются способом аппроксимации эмпирической вариограммы теоретической вариограммой и последующей интерполяцией результатов наблюдений.

5.3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ

ГЕОЛОГИЧЕСКИХ ПОЛЕЙ

5.3.1. Линейная интерполяционная модель

В основе модели лежит предположение о том, что между пунктами измерений значения пространственной переменной меняются по закону прямой линии. При густой сети измерений и слабой изменчивости величин предположение может быть близким к действительности и не повлечет за собой существенных погрешностей при прогнозировании значений между пунктами измерений. Может быть противоположная ситуация, когда величина настолько изменчива, что какое-нибудь разумное предположение о ее поведении между пунктами измерений сделать невозможно. В этом случае линейная модель выбирается из соображений максимальной простоты, что обеспечивает высокую достоверность прогнозирования. Подобные соображения используют, например, для оконтуривания рудных тел при подсчете запасов, когда сложные контуры тел заменяют многоугольниками, состоящими из прямолинейных отрезков.

Если в пункте с координатой х ₁ измерено значение пространственной переменной j₁, в пункте х ₂ – значение j₂, то при линейной интерполяции в любом пункте х между х ₁ и х ₂ интерполированное (прогнозное) значение

.                         (5.5)

Линейную интерполяцию можно представить графически в виде отрезков ломаной линии, опирающейся на измеренные значения j₁, j₂, …, j _n (табл.5.1, рис.5.1).

Таблица 5.1 Предыдущая13141516171819202122232425262728Следующая Поделиться: Воспользуйтесь поиском по сайту: ©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...