Главная | Обратная связь | Поможем написать вашу работу! Архитектура Биология География Искусство История Информатика Маркетинг Математика Медицина Менеджмент Охрана труда Политика Правоотношение Разное Социология Строительство Физика Философия Финансы Химия Экология Экономика Электроника Результаты измерения мощности Рудного тела   Номер пункта Расстояние от начальной точки, м Мощность, м 1 0,0 2,2 2 7,0 1,9 3 20,1 2,5 4 28,6 4,2 5 34,8 3,8 6 44,0 3,1 7 54,9 3,9 8 62,1 2,6

Линейная интерполяция может быть выполнена и в двухмерном пространстве внутри треугольника, образованного тремя пунктами наблюдений, не лежащими на одной прямой. По данным в вершинах треугольника можно найти уравнение плоскости:

j = ах + by + c. (5.6)

Уравнение позволяет вычислять интерполированное значение j в любой точке с заданными координатами х и у внутри треугольника. Если имеется много пунктов наблюдений, то охваченная ими площадь разбивается на несколько треугольников и в каждом из них рассчитывается свое интерполяционное уравнение (5.6).

8 Пример 5.1. Имеются три вертикальные скважины, в которых определены абсолютные отметки кровли пласта (табл.5.2). Необходимо рассчитать абсолютную отметку кровли пласта с координатами х = 240 м, у = 200 м.

Составим систему уравнений:

Решение системы дает коэффициенты а = –0,206; b = –0,341; с = 247,1. Следовательно, интерполяционное уравнение (5.6) имеет вид

z = –0,206 х – 0,341 у + 247,1.

Подставляя в него заданные координаты, найдем абсолютную отметку кровли в точке х = 240 м, у = 200 м:

z = –0,206∙240 – 0,341∙200 + 247,1 = 129,5 м.

Зная коэффициенты уравнения (5.6), из примера можно извлечь дополнительную геологическую информацию об элементах залегания кровли пласта. Азимут простирания a = arctg(– b / a), а угол падения g = arctg . В данном примере имеем a = = arctg(–0,341/0,206) = –59° = 301°, g = arctg 22°.7

Можно распространить линейную интерполяцию и на трехмерное пространство, которое разделяется на совокупность тетраэдров. Каждый тетраэдр образован четырьмя пунктами измерений, не лежащими на одной плоскости. Внутри тетраэдра интерполяция осуществляется с помощью уравнения (гиперплоскости)

j = ах + by + cz + d,

которое опирается на вершины тетраэдра и рассчитывается аналогично приведенному в примере 5.1.

Следует отметить, что линейная интерполяционная модель, как и другие детерминированные модели, не позволяет оценить погрешность интерполяции без привлечения дополнительных данных. Чтобы решить эту задачу, надо выполнить дополнительные измерения пространственной переменной внутри интервалов интерполяции и сравнить интерполированные и измеренные данные. Статистическая обработка таких материалов позволяет выявить, как погрешность интерполяции зависит от расстояния между пунктами наблюдений.

5.3.2. Полиномиальная модель

В основе модели лежит предположение о том, что поведение пространственной переменной нелинейное и может быть описано полиномиальной функцией, значения которой совпадают с фактическими данными в пунктах измерений. Полиномиальная функция может быть одно-, двух- и трехмерной. Простейшая одномерная полиномиальная функция имеет вид

j(х) = a ₀ + a ₁ x + a ₂ x ² + … + a_kx^k.                  (5.7)

Порядок полинома k на единицу меньше числа измерений n.

Полиномиальная модель редко применяется на практике, так как по мере увеличения числа измерений степень полинома растет, а при высоких степенях полинома интерполированные значения вычисляются с большой погрешностью и испытывают столь сильные изменения, что часто переходят границы реальности.

8 Пример 5.2. По данным табл.5.1 необходимо рассчитать полиномиальную модель.

Поскольку таблица содержит восемь пунктов измерений, необходимо иметь полином седьмого порядка. Подобный полином содержит восемь неизвестных коэффициентов, для нахождения которых составим систему из восьми уравнений:

а ₀ + 0,0 а ₁ + 0,0² а ₂ + 0,0³ а ₃ +

+ 0,0⁴ а ₄ + 0,0⁵ а ₅ + 0,0⁶ а ₆ +

+ 0,0⁷ а ₇ = 2,2;

а ₀ + 7,0 а ₁ + 7,0² а ₂ + 7,0³ а ₃ +

+ 7,0⁴ а ₄ + 7,0⁵ а ₅ + 7,0⁶ а ₆ +

+ 7,0⁷ а ₇ = 1,9;

а ₀ + 20,1 а ₁ + 20,1² а ₂ + 20,1³ а ₃ + 20,1⁴ а ₄ + 20,1⁵ а ₅ + 20,1⁶ а ₆ + 20,1⁷ а ₇ = 2,5;

а ₀ + 28,6 а ₁ + 28,6² а ₂ + 28,6³ а ₃ + 28,6⁴ а ₄ + 28,6⁵ а ₅ + 28,6⁶ а ₆ + 28,6⁷ а ₇ = 4,2;

а ₀ + 34,8 а ₁ + 34,8² а ₂ + 34,8³ а ₃ + 34,8⁴ а ₄ + 34,8⁵ а ₅ + 34,8⁶ а ₆ + 34,8⁷ а ₇ = 3,8;

а ₀ + 44,0 а ₁ + 44,0² а ₂ + 44,0³ а ₃ + 44,0⁴ а ₄ + 44,0⁵ а ₅ + 44,0⁶ а ₆ + 44,0⁷ а ₇ = 3,1;

а ₀ + 54,9 а ₁ + 54,9² а ₂ + 54,9³ а ₃ + 54,9⁴ а ₄ + 54,9⁵ а ₅ + 54,9⁶ а ₆ + 54,9⁷ а ₇ = 3,9;

а ₀ + 62,1 а ₁ + 62,1² а ₂ + 62,1³ а ₃ + 62,1⁴ а ₄ + 62,1⁵ а ₅ + 62,1⁶ а ₆ + 62,1⁷ а ₇ = 2,6.

Решение системы дает коэффициенты а ₀, а ₁, а ₂, ¼, а ₇, которые позволяют составить уравнение полинома (5.7) и построить график (рис.5.2). Численные значения по осям графика такие же, как на рис.5.1.7

5.3.3. Модель обратных расстояний

В основу модели положена идея о том, что влияние измерений убывает обратно пропорционально квадрату расстояния r от пункта измерения (как в законе всемирного тяготения или в электрическом поле заряженных частиц), поэтому модель часто называют потенциальной. Интерполированное значение j в каждой точке находят как средневзвешенное из измеренных значений в соседних пунктах n:

                                 (5.8)

Если расстояние r равно нулю, то в данном пункте принимается измеренное фактическое значение. Для прогнозирования берут три-пять ближайших пунктов измерений или ограничиваются каким-то произвольным радиусом R. В расчет принимают все пункты измерений в пределах этого радиуса. За пределами радиуса влияние измеренных значений не учитывается.

8 Пример 5.3. Используя данные табл.5.1, построим интерполяционную модель обратных расстояний (рис.5.3).

Все расчеты проведем по четырем соседним пунктам измерений. Вначале берем первые четыре пункта и по формуле (5.8) находим значения кривой между первым и третьим пунктами. Далее, чтобы найти значения кривой между третьим и четвертым пунктами, необходимо брать в расчет слева и справа по два пункта (второй, третий, четвертый и пятый). Передвигаясь далее на один пункт, повторим расчеты по следующим четырем пунктам (с третьего по шестой). В результате получим кривую между четвертым и пятым пунктами. Подобные операции повторяют до конечного пункта. Такой прием называется «расчет в скользящем окне размером в четыре наблюдения». Полученные результаты представлены на рис.5.3. Численные значения по осям графика такие же, как на рис.5.1.

На графике виден недостаток метода обратных расстояний. В пунктах измерения касательная к кривой всегда горизонтальная, что не соответствует действительности. Тем не менее, метод широко применяется на практике, когда другие методы не работают.7

5.3.4. Сплайн-модель

Сплайн – это кусочно-непрерывная гладкая функция, состоящая из множества полиномиальных функций третьего порядка, плавно переходящих друг в друга. Сплайн позволяет построить плавный график пространственной переменной, хорошо согласующийся с геологическими представлениями, и поэтому весьма популярен. Его можно уподобить гибкой упругой линейке, опирающейся на ординаты фактических значений пространственной переменной. Концы линейки могут быть свободными или закрепленными с заданным углом наклона. Сплайн бывает одно-, двух- и трехмерным.

Рассмотрим методику расчета одномерного сплайна. Пусть имеется n пунктов измерений с координатами х ₁, х ₂, …, х_n. В каждом пункте измерено значение пространственной переменной j₁, j₂, …, j _n. Между пунктами измерений имеется n – 1 отрезок. Каждый отрезок представлен полиномом третьего порядка:

j = а + bx + cx ² + dx ³.                          (5.9)

В каждом полиноме четыре неизвестных коэффициента a, b, с, d. Следовательно, всего имеем 4(n – 1) неизвестный коэффициент. Их нужно подобрать такими, чтобы выполнялись следующие условия:

· в пунктах х ₁, х ₂, …, х_n значения полиномов должны совпадать с измеренными значениями j₁, j₂, …, j _n;

· в пунктах стыковки соседних полиномов х ₂, х ₃, …, х_{n- 1} не должно быть изломов, т.е. наклоны линий должны быть одинаковыми, что сводится к равенству первых производных от полиномов (5.9);

· в тех же пунктах стыковки не должно быть скачка кривизны, что соответствует равенству вторых производных от полиномов (5.9);

· в начальном и конечном пунктах должны быть заданы граничные условия.

Нахождение коэффициентов a, b, с, d сводится к решению системы 4(n – 1) уравнения первой степени, которые получаются следующим образом.

Каждое значение полинома должно совпадать с левым измеренным значением каждого отрезка пространственной переменной, что дает n – 1 уравнение:

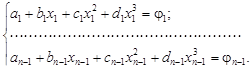
Каждое значение полинома должно совпадать с правым измеренным значением каждого отрезка пространственной переменной, что дает еще n – 1 уравнение:

В n – 2 пунктах стыковки должны быть равны первые производные соседних полиномов (j¢ = b + 2 cx + 3 dx ²) – равенство касательных:

В тех же n – 2 пунктах стыковки должны быть равны вторые производные соседних полиномов (j¢¢ = 2 с + 6 dx) – равенство кривизны:

Нужны еще два уравнения, учитывающие граничные условия в конечных пунктах х ₁ и х_n. Чаще других применяется условие, что в конечных пунктах кривизна нулевая (концы упругой линейки не закреплены), т.е. вторые производные должны быть нулевыми:

Могут быть заданы и другие условия, например наклон касательной (т.е. первой производной) в крайних пунктах.

В результате получится необходимое число уравнений 4(n – 1). Решение системы уравнений дает все необходимые коэффициенты полиномов, что позволяет рассчитывать (прогнозировать) значения пространственной переменной между пунктами измерений.

При большом числе пунктов измерений получается довольно громоздкая система уравнений первой степени, и, хотя ее решение на компьютере не составляет труда, объем вычислений довольно значителен.

Чтобы избежать большого объема вычислений, рекомендуется применять скользящий сплайн. Для скользящего сплайна берут четыре или шесть смежных пунктов измерений, по ним рассчитывают уравнения сплайна, а для построения и прогнозирования выбирают один полином, занимающий среднее положение. Потом осуществляется перемещение на один пункт измерения (скольжение) и расчет повторяется. Эти операции доводят до конечного пункта измерений. Исключение делается для первого отрезка, для которого используют первое уравнение, и для последнего отрезка, для которого используют последнее уравнение.

8 Пример 5.4. По данным табл.5.1 необходимо рассчитать скользящий сплайн.

Возьмем первые шесть пунктов измерений и составим необходимую систему уравнений. Между шестью пунктами имеются пять отрезков, следовательно, нужно рассчитать пять кубических полиномов, содержащих 20 коэффициентов.

Первое условие – все полиномы должны проходить через левую точку отрезков:

а ₁₁ + a ₁₂ + а ₁₃ + а ₁₄ = 2,2;

а ₂₁ + 7,0 а ₂₂ + 7,0² а ₂₃ + 7,0³ а ₂₄ = 1,9;

а ₃₁ + 20,1 а ₃₂ + 20,1² а ₃₃ + 20,1³ а ₃₄ = 2,5;

а ₄₁ + 28,6 а ₄₂ + 28,6² а ₄₃ + 28,6³ а ₄₄ = 4,2;

а ₅₁ + 34,8 а ₅₂ + 34,8² а ₅₃ + 34,8³ а ₅₄ = 3,8.

Все полиномы должны проходить через правую точку отрезков:

а ₁₁ + 7,0 a ₁₂ + 7,0² а ₁₃ + 7,0³ а ₁₄ = 1,9;

а ₂₁ + 20,1 а ₂₂ + 20,1² а ₂₃ + 20,1³ а ₂₄ = 2,5;

а ₃₁ + 28,6 а ₃₂ + 28,6² а ₃₃ + 28,6³ а ₃₄ = 4,2;

а ₄₁ + 34,8 а ₄₂ + 34,8² а ₄₃ + 34,8³ а ₄₄ = 3,8;

а ₅₁ + 44,0 а ₅₂ + 44,0² а ₅₃ + 44,0³ а ₅₄ = 3,1.

Второе условие – на стыках соседних отрезков должны быть равны первые производные:

a ₁₂ + 2∙7,0 а ₁₃ + 3∙7,0² а ₁₄ = а ₂₂ + 2∙7,0 а ₂₃ + 3∙7,0² а ₂₄;

а ₂₂ + 2∙28,6 а ₂₃ + 3∙28,6² а ₂₄ = а ₃₂ + 2∙28,6 а ₃₃ + 3∙28,6² а ₃₄;

а ₃₂ + 2∙34,8 а ₃₃ + 3∙34,8² а ₃₄ = а ₄₂ + 2∙34,8 а ₄₃ + 3∙34,8² а ₄₄;

а ₄₂ + 2∙44,0 а ₄₃ + 3∙44,0² а ₄₄ = а ₅₂ + 2∙44,0 а ₅₃ + 3∙44,0² а ₅₄.

Третье условие – на стыках соседних отрезков должны быть равны вторые производные:

2 а ₁₃ + 6∙7,0 а ₁₄ = 2 а ₂₃ + 6∙7,0 а ₂₄;

2 а ₂₃ + 6∙28,6 а ₂₄ = 2 а ₃₃ + 6∙28,6 а ₃₄;

2 а ₃₃ + 6∙34,8 а ₃₄ = 2 а ₄₃ + 6∙34,8 а ₄₄;

2 а ₄₃ + 6∙44,0 а ₄₄ = 2 а ₅₃ + 6∙44,0 а ₅₄.

Четвертое условие – на свободных концах первого и последнего отрезков примем граничные условия – вторые производные равны нулю:

2 а ₁₃ + 6∙0,0 а ₁₄ = 0;

2 а ₅₃ + 6∙44,0 а ₅₄ = 0.

Всего получено 20 уравнений первой степени с 20 неизвестными коэффициентами. Решение системы дает значения коэффициентов:

а ₁₁ = 2,200000; а ₁₂ = –0,069706; а ₁₃ = 0,005753; а ₁₄ = 0,000274;

а ₂₁ = 1,955657; а ₂₂ = 0,035012; а ₂₃ = –0,009206; а ₂₄ = 0,000438;

а ₃₁ = 21,556675; а ₃₂ = –2,890512; а ₃₃ = 0,136342; а ₃₄ = –0,001975;

а ₄₁ = –73,310478; а ₄₂ = 7,060588; а ₄₃ = –0,211599; а ₄₄ = 0,002080;

а ₅₁ = 22,811948; а ₅₂ = 1,225829; а ₅₃ = 0,026517; а ₅₄ = –0,000201.

Далее происходит перемещение исходных измерений на один шаг, все расчеты повторяют. Перемещение доводится до конца исходных данных. Конечный результат виден на рис.5.4. Очевидно преимущество полученного графика перед графиками рис.5.2 и 5.3.7

Более сложным является расчет двухмерного сплайна. В литературе не удалось найти полное решение двухмерного сплайна для произвольно расположенных пунктов измерений. Имеющиеся публикации рассчитаны только на прямоугольную сеть, причем вычисляются сплайны в двух перпендикулярных направлениях, а в промежутках между ними используется интерполяция.

Теоретически можно построить и трехмерный сплайн, но на практике его, по-видимому, не применяют.

ВЕРОЯТНОСТНЫЕ МОДЕЛИ

ГЕОЛОГИЧЕСКИХ ПОЛЕЙ

5.4.1. Модель на основе случайной функции

Основой случайной функции служит предположение, что измеренные значения являются случайными функциями координат и содержат две составляющие: математическое ожидание m (x) (закономерная изменчивость, или тренд) и случайные колебания d(x) относительно его [см. формулу (5.2)].

Если математическое ожидание – величина постоянная, то случайная функция называется стационарной, в противном случае – нестационарной. Математическое ожидание позволяет прогнозировать значения пространственной переменной между пунктами измерений, тогда как случайные колебания служат для оценки погрешности прогнозирования.

Стационарная случайная функция может обладать еще одним свойством. Если на любом ее отрезке характеристики одинаковые, то функция эргодичная, что редко используется в геологической практике.

Измеренные значения в отдельных точках называются реализациями случайной функции. Случайную функцию можно изобразить на графике, на котором точки пунктов измерений имеют случайные отклонения d от плавной линии математического ожидания m (x) (рис.5.5). Отклонения бывают положительные, отрицательные и нулевые.

Случайная функция имеет три главные характеристики: математическое ожидание, дисперсию случайных колебаний и автокорреляционную функцию.

Математическое ожидание может рассматриваться как тренд, заданный на основе теоретических соображений (зависимость плотности от состава руды, кривая радиоактивного распада) или эмпирическим способом, чаще всего в виде полинома. Эмпирический полином является приближенной оценкой математического ожидания. Вычисление тренда осуществляется по методу наименьших квадратов (см. подраздел 3.1.5), а наилучший порядок полинома находят согласно подразделу 4.1.3. Возможен еще один метод оценки математического ожидания путем сглаживания исходных данных способом скользящего окна.

Математическое ожидание стационарной случайной функции, как отмечалось, величина постоянная и равная среднеарифметическому из всех измеренных значений. Если из нестационарной случайной функции вычесть математическое ожидание, то, согласно формуле (5.2), она превратится в стационарную с нулевым математическим ожиданием. Во многих случаях математическое ожидание (закономерная изменчивость, или тренд) слабо проявлено, тогда им пренебрегают, полагая случайную функцию стационарной.

Дисперсия случайной функции равна дисперсии отклонений d(х):

.                             (5.10)

Если из дисперсии извлечь квадратный корень, то можно получить среднеквадратичное отклонение s_d.

Автоковариационная функция

,                     (5.11)

где m – количество слагаемых под знаком суммы; h – шаг измерений.

Особый интерес представляет автокорреляционная функция

.                                (5.12)

Она является аналогом коэффициента корреляции случайных величин, колеблется в пределах от –1 до +1 и характеризует зависимость между отклонениями d на расстоянии h.

Автокорреляционная функция зависит от шага измерений h. При нулевом шаге она равна единице, при увеличении шага убывает, приближаясь к нулю. В идеальном виде функция показана на рис.5.6. Шаг, при котором автокорреляционная функция неотличима от нуля, называется радиусом автокорреляции R. Он является важной величиной, характеризующей радиус влияния отдельного измерения.

Следует отметить, что шаг и радиус автокорреляции являются векторными величинами. В изотропной среде радиус влияния одинаков по всем направлениям. В анизотропной среде, а геологические объекты – большей частью анизотропные тела, радиус автокорреляции зависит от направления. Чем сильнее проявлена изменчивость в каком-либо направлении, тем меньше радиус автокорреляции.

Таблица 5.3 Предыдущая13141516171819202122232425262728Следующая Поделиться: Воспользуйтесь поиском по сайту: ©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...