 |
Результаты измерений пространственной переменной
|
|
|
|
И некоторые вычисленные данные
| Номер пункта n | Исходные измерения f (x) | Среднее значение a 0/2 | Отклонение d0(x) | Первая гармоника w1(x) | Отклонение d1(x) | Вторая гармоника w2(x) | Отклонение d2(x) | |
| 1 | 2,36 | 3,14 | –0,78 | 0,34 | –1,12 | –0,38 | –0,74 | |
| 2 | 2,08 | 3,14 | –1,06 | 0,31 | –1,37 | –0,30 | –1,07 | |
| 3 | 1,95 | 3,14 | –1,19 | 0,26 | –1,45 | –0,14 | –1,31 | |
| 4 | 7,68 | 3,14 | 4,54 | 0,20 | 4,34 | 0,05 | 4,29 | |
| 5 | 5,72 | 3,14 | 2,58 | 0,12 | 2,46 | 0,23 | 2,23 | |
| 6 | 3,08 | 3,14 | –0,06 | 0,03 | –0,09 | 0,35 | –0,44 | |
| 7 | 2,20 | 3,14 | –0,94 | –0,06 | –0,88 | 0,38 | –1,26 | |
| 8 | 2,76 | 3,14 | –0,38 | –0,14 | –0,24 | 0,30 | –0,54 | |
| 9 | 1,32 | 3,14 | –1,82 | –0,22 | –1,60 | 0,14 | –1,74 | |
| 10 | 1,02 | 3,14 | –2,12 | –0,28 | –1,84 | –0,05 | –1,79 | |
| 11 | 3,24 | 3,14 | 0,10 | –0,32 | 0,42 | –0,23 | 0,65 | |
| 12 | 4,90 | 3,14 | 1,76 | –0,34 | 2,10 | –0,35 | 2,45 | |
| 13 | 4,48 | 3,14 | 1,34 | –0,34 | 1,68 | –0,38 | 2,05 | |
| 14 | 2,30 | 3,14 | –0,84 | –0,31 | –0,53 | –0,30 | –0,23 | |
| 15 | 1,97 | 3,14 | –1,17 | –0,26 | –0,91 | –0,14 | –0,77 | |
| 16 | 2,27 | 3,14 | –0,87 | –0,20 | –0,67 | 0,05 | –0,73 | |
| 17 | 2,08 | 3,14 | –1,06 | –0,12 | –0,94 | 0,23 | –1,18 | |
| 18 | 1,45 | 3,14 | –1,69 | –0,03 | –1,66 | 0,35 | –2,01 | |
| 19 | 3,85 | 3,14 | 0,71 | 0,06 | 0,65 | 0,38 | 0,28 | |
| 20 | 5,18 | 3,14 | 2,04 | 0,14 | 1,90 | 0,30 | 1,60 | |
| 21 | 6,34 | 3,14 | 3,20 | 0,22 | 2,98 | 0,14 | 2,84 | |
| 22 | 3,93 | 3,14 | 0,79 | 0,28 | 0,51 | –0,05 | 0,57 | |
| 23 | 2,33 | 3,14 | –0,81 | 0,32 | –1,13 | –0,23 | –0,89 | |
| 24 | 2,11 | 3,14 | –1,03 | 0,34 | –1,37 | –0,35 | –1,02 | |
| 25 | 1,90 | 3,14 | –1,24 | 0,34 | –1,58 | –0,38 | –1,20 | |
|
|
| |||||||
| Дисперсия |
| 2,790 | - | 2,734 | - | 2,666 | ||
Отклонения δ(х) дают возможность вычислить остаточные дисперсии:
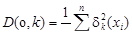, (5.22)
которые образуют убывающий ряд.
Разность соседних остаточных дисперсий дает дисперсию текущей гармоники k:
. (5.23)
Ее можно выразить в процентах от дисперсии пространственной переменной D = 2,790, принимаемой за 100 %.
Для вычисления гармоник, часть которых приведена в табл.5.7, применим преобразованную формулу (5.14):
. (5.24)
|
|
|
Таблица 5.8
Результаты расчета всех гармоник
| Номер гармоники k | Длина волны L / k | Коэффициент | Ампли-туда A | Дисперсия отклонений D (o, k) | Дисперсия гармоник | ||||
| аk | bk | D (k) | D (k),% | ||||||
| 0 | – | 3,140 | 0,000 | 0,000 | 2,790 | 0,000 | 0,0 | ||
| 1 | 24,0 | 0,335 | –0,058 | 0,340 | 2,734 | 0,056 | 2,0 | ||
| 2 | 12,0 | –0,376 | 0,054 | 0,380 | 2,665 | 0,070 | 2,5 | ||
| 3 | 8,0 | –1,828 | 0,535 | 1,905 | 0,912 | 1,753 | 62,8 | ||
| 4 | 5,0 | –0,154 | –0,070 | 0,169 | 0,898 | 0,014 | 0,5 | ||
| 5 | 4,8 | 0,084 | 0,040 | 0,093 | 0,894 | 0,004 | 0,2 | ||
| 6 | 4,0 | 0,597 | –0,883 | 1,066 | 0,317 | 0,577 | 20,7 | ||
| 7 | 3,4 | 0,469 | 0,042 | 0,471 | 0,210 | 0,107 | 3,8 | ||
| 8 | 3,0 | 0,241 | 0,178 | 0,300 | 0,166 | 0,044 | 1,6 | ||
| 9 | 2,7 | –0,041 | 0,128 | 0,135 | 0,156 | 0,009 | 0,3 | ||
| 10 | 2,4 | –0,146 | 0,263 | 0,301 | 0,110 | 0,046 | 1,7 | ||
| 11 | 2,2 | –0,243 | 0,326 | 0,406 | 0,027 | 0,084 | 3,0 | ||
| 12 | 2,0 | –0,088 | 0,000 | 0,088 | 0,027 | 0,000 | 0,0 | ||
|
| |||||||||
| Сумма | – | – | – | – | – | 2,764 | 99,1 | ||
|
|
Коэффициенты ak и bk позволяют рассчитать амплитуды всех гармоник по формуле (5.16), а отклонения – их дисперсии по формуле (5.22).
Результаты расчетов по всем 12 гармоникам суммированы в табл.5.8. Отметим, что отношение L / k – это длина волны гармоники k. В таблице приведены длина волны, коэффициенты ak и bk, амплитуда А, дисперсии отклонений D (o, k), их разности – дисперсии гармоник D (k) и они же, выраженные в процентах от дисперсии пространственной переменной.
Вычисления показали, что главное значение имеют третья гармоника с длиной волны 8 м (рис.5.12, б), ее доля составляет 62,8 %, и шестая гармоника с длиной волны 4 м (рис.5.12, в), ее доля 20,7 %. Остальные гармоники играют малую роль.
Следовательно, можно ограничиться двумя важнейшими гармониками, которые в сумме дают 83,5 % от дисперсии пространственной переменной (рис.5.12, г).
Данные табл.5.8 позволяют построить спектр амплитуд (рис.5.13).7
5.4.3. Периодограммный анализ
Периодическая изменчивость не обязательно должна быть синусоидальной, она может иметь любую форму. Можно выявить периодическую изменчивость любой формы путем последовательного перебора длин волн, кратных шагу наблюдений. Такая методика, по-видимому, не описана в литературе. Предлагается назвать ее периодограммным анализом.
|
|
|
Таблица 5.9
Расчет периодической изменчивости
и отклонений при длине волны L = 5 м
| Номер столбца | ||||
| 1 | 2 | 3 | 4 | 5 |
| Исходные данные | ||||
| 2,36 | 2,08 | 1,95 | 7,68 | 5,72 |
| 3,08 | 2,20 | 2,76 | 1,32 | 1,02 |
| 3,24 | 4,90 | 4,48 | 2,30 | 1,97 |
| 2,27 | 2,08 | 1,45 | 3,85 | 5,18 |
| 6,34 | 3,93 | 2,33 | 2,11 | 1,90 |
| Средние по столбцам (периодическая изменчивость) | ||||
| 3,46 | 3,04 | 2,59 | 3,45 | 3,16 |
| Отклонения от средних | ||||
| –1,10 | –0,96 | –0,64 | 4,23 | 2,56 |
| –0,38 | –0,84 | 0,17 | –2,13 | –2,14 |
| –0,22 | 1,86 | 1,89 | –1,15 | –1,19 |
| –1,19 | –0,96 | –1,14 | 0,40 | 2,02 |
| 2,88 | 0,89 | –0,26 | –1,34 | –1,26 |
| ________________ Дисперсия исходных данных 2,790 | ||||
| Дисперсия отклонений 2,689 | ||||
| Дисперсия периодической изменчивости 0,101 | ||||
