Способ относительных разниц

Способ цепной подстановки

Определение величины влияния отдельных факторов на при­рост результативных показателей является одной из важнейших методологических задач в АХД. В детерминированном анализе для этого используются следующие способы: цепной подстановки, аб­солютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования, балансовый и др.

Наиболее универсальным из них является способ цепной подстанов­ки. Он используется для расчета влияния факторов во всех типах де­терминированных факторных моделей: аддитивных, мультиплика­тивных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме резуль­тативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных значений результативного показа­теля, которые учитывают изменение одного, затем двух, трех и по­следующих факторов, допуская, что остальные не меняются. Срав­нение значений результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя. Порядок применения этого способа рассмотрим на примере, приведенном в табл. 4.1.

Как нам уже известно, объем валового выпуска продукции (ВП) зависит от двух основных факторов первого порядка: численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфактор- ную мультипликативную модель:

ВП = ЧР ГВ.

Алгоритм расчета способом цепной подстановки для этой мо­дели:

ВП₀ = ЧР₀ • ГВ₀ = 100 • 4 = 400 млн руб.;

ВП_усл= ЧРу ■ ГВ₀ = 120 -4 = 480 млн руб.; ВП₂ = ЧР, • TBj = 120 • 5 = 600 млн руб.

Таблица 4.1 Показатель Условное обозначе­ние Уровень показателя Изменение базовый текущий абсолют­ное относи­тельное, % Валовой выпуск продукции, млн руб. ВП     +150 +50 Среднесписочная численность рабочих ЧР     +20 +20 Среднегодовая выра­ботка продукции одним рабочим, млн руб. ГВ     +1 +25 Количество отрабо- тай­ных дней одним рабочим за год Д   208,3 +8,3 +4,17 Среднедневная выра­ботка рабочего, тыс. руб. ДВ     +4 +20 Средняя продолжи­тельность смены, ч П   7,5 -0,5 -5 Среднечасовая выра­ботка продукции одним рабочим, тыс. руб. ЧВ 2,5 3,2 +0,7 +28

 

Как видим, второй показатель выпуска продукции отличается от первого тем, что при его расчете принята численность рабочих текущего периода вместо базового. Среднегодовая выработка про- ' дукции одним рабочим в том и другом случае базовая. Значит, за счет роста численности рабочих выпуск продукции увеличился на ' 80 млн руб. (480-400).

Данные для факторного анализа валового выпуска продукции

Третий показатель выпуска продукции отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо базового. Количество же работников в обоих случаях — отчетного периода. Отсюда за счет повышения производительности труда выпуск продукции увеличился на 120 млн руб. (600-480).

Таким образом, увеличение выпуска продукции вызвано следу­ющими факторами:

а) рост численности рабочих + 80 млн руб.;

б) повышение уровня производительности

труда +120 млн руб.

Итого + 200 млн руб.

Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:

АВП_чр + АВП_гв = АВП_общ.

Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.

Если требуется определить влияние четырех факторов, то в этом случае рассчитывается не один, а три условных значения результа­тивного показателя, т.е. количество условных значений результа­тивного показателя на единицу меньше числа факторов. Схемати­чески это можно представить следующим образом.

Уровень результативного показателя	Условия расчета результативного показателя
Фактор 1	Фактор II	Фактор III	Фактор IV
Базовый	'о	'о	Ч)	'о
Условный 1	*1	1о	'о	'о
Условный 2	ч		'0	'о
Условный 3"	ч	м		ч>
Текущий	ч	11

 

Общее изменение результативного показателя:

AY_o6ui=Y,-Y₀,

в том числе за счет:

л у =v — Y ■ AY = Y -Y

А усл1 ^I0' ^ziIB усл2 уел 1'

AY =Y -Y • AY =Y - Y

С ^слЗ усл2> ^ziID M услЗ"

Проиллюстрируем это на четырехфакторной модели выпуска продукции:

ВП = ЧР д п чв.

Исходные данные для решения задачи приведены в табл. 4.1: ВП₀ = ЧР₀ ■ Д₀ • П₀ • ЧВ₀ = 100 • 200 • 8 • 2,5 = 400 млн руб.;

ВП_усл1 = ЧР, • До • п₀ • ЧВ₀= 120 • 200 • 8 ■ 2,5 = 480 млн руб.;

ВГ1_усл2 - ЧР, • Д₁ • П₀ • ЧВ₀ = 120 • 208,3 ■ 8 • 2,5 = 500 млн руб.;

ВП_усл3 = ЧР, • Д; • П, • ЧВ₀ = 120 • 208,3 • 7,5 ■ 2,5 = = 468,75 млн руб.;

ВП, = ЧР, • Д, • П, • ЧВ, = 120 • 208,3 • 7,5 • 3,2 = 600 млн руб.

Объем выпуска продукции в целом вырос на 200 млн руб. (600 — 400), в том числе за счет изменения:

а) количества рабочих

ДВП_чр= ВП_усл, - ВП₀ = 480 - 400 = +80 млн руб.;

б) количества отработанных дней одним рабочим за год

АВП_Д = ВП_усл2 - ВП_усл1 = 500 - 480 = +20 млн руб.;

в) средней продолжительности рабочего дня

АВП_п = ВП_усл3 - ВП_усл2 = 468,75 - 500 = -31,25 млн руб.;

г) среднечасовой выработки

ДВП_чв = ВП, - ВП_усл3 = 600 - 468,75 = +131,25 млн руб.

Итого +200 млн руб.

Используя способ цепной подстановки, необходимо знать правила последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько каче­ственных показателей, то сначала следует изменить величину фак­торов первого порядка, а потом более низкого. В приведенном примере объем производства продукции зависит от четырех фак­торов: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выра­ботки. Согласно рис. 2.3 количество рабочих по отношению к ва­ловому выпуску продукции — фактор первого уровня, количество отработанных дней — второго уровня, продолжительность рабоче­го дня и среднечасовая выработка — факторы третьего уровня: Это и обусловило последовательность размещения факторов в модели и, соответственно, очередность определения их влияния.

Таким образом, применение способа цепной подстановки тре­бует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.

Способ абсолютных разниц

Способ абсолютных разниц применяется для расчета влияния факторов на прирост результативного показателя в детерминиро­ванном анализе, но только в мультипликативных моделях (Y = х, х

х х₂ • х₃..... х_п) и моделях мультипликативно-аддитивного типа:

Y= (а — Ь)с и Y = а(Ь — с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД.

При его использовании величина влияния факторов рассчиты­вается умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые на­ходятся справа от него, и на фактическую величину факторов, рас­положенных слева от него в модели.

Алгоритм расчета для мультипликативной четырехфакторной мо­дели валового выпуска продукции выглядит следующим образом:

ВП = ЧР Д П ЧВ.

ДВП_чр = ДЧР • До • п₀ • ЧВ₀ = (+20) ■ 200 • 8,0 • 2,5 = +80 000;

ДВПд = 4Pj • ДД • П₀ • ЧВ₀ = 120 • (+8,33) • 8,0 • 2,5 = +20 000;

ДВП_п = ЧР, ■ Д, • ДП ■ ЧВ₀ = 120 • 208,33 ■ (-0,5) • 2,5 = -31 250;

ДВП_чв = 4Pj • Д_х • П] • ДЧВ = 120 • 208,33 • 7,5 • (+0,7) = +131 250

Итого +200 000

Таким образом, с помощью способа абсолютных разниц полу­чаются те же результаты, что и способом цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сум­ма прироста результативного показателя за счет отдельных факто­ров равнялась его общему приросту.

Рассмотрим алгоритм расчета факторов этим способом в моделях мультипликативно-аддитивного вида. Для примера возьмем фак­торную модель прибыли от реализации продукции:

П = УРП(Ц-С), где П — прибыль от реализации продукции;

УРП — объем реализации продукции;

Ц — цена единицы продукции;

С — себестоимость единицы продукции.

Прирост суммы прибыли за счет изменения:

объема реализации продукции ДП_урп = ДУРП (Ц₀ — С₀);

Способ относительных разниц

Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях. Здесь используются относитель­ные приросты факторных показателей, выраженные в виде коэф­фициентов или процентов. Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y= abc.

Дс

Изменение результативного показателя определяется следу­ющим образом:

 

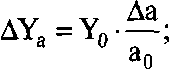
AY_b=(Y₀ + AY

AY_c=(Y₀+AY_a+AY_b)^

Согласно данному алгоритму для расчета влияния первого фак­тора необходимо базовую величину результативного показателя умножить на относительный прирост первого фактора, выражен­ного в виде десятичной дроби.

Чтобы рассчитать влияние второго фактора, нужно к базовой величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на от­носительный прирост второго фактора.

Влияние третьего фактора определяется аналогично: к базовой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.

ДПц = УРП, • АЦ; ДПС = УРП, (—ДС).

цены реализации себестоимости продукции

Закрепим рассмотренную методику на примере, приведенном в табл. 4.1:

 

ДЧР

----- = 400----- = +80 млн руб.;

ДВПЦР=ВП,

чр

о

ЧР_П 100

 

8,33

ДВПд = (ВП₀ + ДВП_ЧР) • = (400 + 80) • = +20 млн руб.;

3 Анализ хоз.деятельности пред.

ДВП_п = (вп₀ + ДВП_ЧР + ДВПд) ■ — = (400 + 80 + 20) • =

П_п 8

^Lo

= -31,25 млн руб.;

о

ДЧВ

ДВП_чв = (вп₀ + ДВП_ЧР + ДВПд + ДВПд) ■

ЧВ

= (400 + 80 + 20-31,25)=+131,25 млн руб.

2,5

Как видим, результаты расчетов такие же, как и при использо­вании предыдущих способов.

Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитывать влияние большого комплекса факто­ров (8—10 и более). В отличие от предыдущих способов здесь значи­тельно сокращается число вычислительных процедур, что обуслов­ливает его преимущество.

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: