Проверка эффективности применявшейся методики тренировки

Для проверки эффективности методики тренировки выдвигаем гипотезы:

– нулевую – H₀: об отсутствии различия между средним исходным показателем скоростных качеств и средним показателем скоростных качеств , достигнутым после двух месяцев тренировок ();

– конкурирующую – H₁: о наличии разницы между ними ().

Предположение об ухудшении скоростных качеств после тренировок, т.е. о том, что , в данном случае лишено здравого смысла, поэтому мы имеем дело с односторонней критической областью.

Ранее мы получили, что s_d ² = 26 уд². Следовательно,

уд.

Наблюдаемое значение t -критерия Стьюдента равно:

.

По таблице (Приложение 4) ищем t_крит для a = 0,05, числа степеней свободы k = n – 1 = 10 – 1 = 9 и односторонней критической области. Находим, что t_крит = 1,83. Сравнение t_набл и t_крит позволяет сделать вывод: так как t_набл (3,10) > t_крит (1,83), с вероятностью 95% (a = 0,05) должна быть принята конкурирующая гипотеза (H₁: ). Следовательно, применение данной методики развития скоростных качеств у спортсменов эффективно. Средний исходный показатель скоростных качеств статистически достоверно увеличился на 5,0 ударов.

 

Расчет и построение доверительного интервала для генеральной средней арифметической

Так как распределение выборки d, составленной из разностей парных значений, согласуется с нормальным законом распределения, а генеральная дисперсия d_i неизвестна, точные значения границ доверительного интервала, в котором с доверительной вероятностью P будет находиться среднее арифметическое значение генеральной совокупности , найдем из следующего двойного неравенства:

Для рассматриваемой задачи оно будет иметь вид:

По таблице критерия Стьюдента (Приложение 4) мы нашли, что для уровня значимости a = 0,05, числа степеней свободы k = n – 1 = 10 – 1 = 9 и двухсторонней критической области t_a = 2,26.

Стандартную ошибку среднего арифметического найдем по формуле:

уд.

Доверительный интервал для среднего арифметического прироста количества ударов за 10 с в генеральной совокупности равен:

1,35 уд. 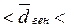8,65 уд.

Следовательно, с доверительной вероятностью P = 0,95 можно утверждать, что в результате тренировки улучшение показателя скоростных качеств будет находиться в пределах от 1,35 до 8,65 ударов за 10 с.

Для построения доверительного интервала необходимо выбрать масштаб. Выберем масштаб 1 уд ≡ 1 см.

 

Доверительный интервал для

Вариант 2: критерий непараметрический

Примечание: В качестве примера возьмем приведенные в таблице 5.4 результаты измерения показателя скоростных качеств у спортсменов перед началом тренировок (они обозначены индексом В, были получены в результате измерений на I этапе деловой игры) и после двух месяцев тренировок (они обозначены индексом Г).

 

От выборок В и Г перейдем к выборке, составленной из разностей парных значений d_i = N_i^Г – N_i^В и определим квадраты этих разностей. Данные занесем в расчетную таблицу 5.4.

 

Таблица 5.4 – Расчет квадратов парных разностей значений d_i²

№ п/п	NiВ, уд	NiГ, уд	di = NiГ – NiВ, уд	di2, уд2
			-7
			-5
			-1
			S = 27	S = 347

 

Пользуясь таблицей 5.4, найдем среднее арифметическое парных разностей:

уд.

Далее рассчитаем сумму квадратов отклонений d_i от по формуле:

уд.²

Определим дисперсию для выборки d_i:

уд.²

Далее необходимо выборку, составленную из разностей парных значений d_i, проверить на нормальность распределения.

Выдвигаем гипотезы:

– нулевую – H₀: о том, что генеральная совокупность парных разностей d_i имеет нормальное распределение;

– конкурирующую – H₁: о том, что распределение генеральной совокупности парных разностей d_i отлично от нормального.

Проверку проводим на уровне значимости a = 0,05.

Для этого составим расчетную таблицу 5.3.

Порядок заполнения таблицы 5.5 аналогичен порядку заполнения таблицы 5,3 и был описан в первом варианте выполнения V этапа.

 

 

Таблица 5.5 – Данные расчета критерия Шапиро и Уилка W_набл для выборки, составленной из разностей парных значений d_i

№ п/п	di, уд	k	dn - k + 1-dk=Dk	ank	Dk×ank
	-7		8 – (–7) = 15	0,5739	8,6085
	-5		7 – (–5) = 12	0,3291	3,9492
	-1		7 – (–1) = 8	0,2141	1,7128
			7 – 0 = 7	0,1224	0,8568
			6 – 5 = 1	0,0399	0,0399

 

По таблице 5.5 находим:

;

.

Наблюдаемое значение критерия W_набл находим по формуле:

.

Проверим правильность выполнения расчетов критерия Шапиро и Уилка (W_набл) его расчетом на ПЭВМ по программе «Статистика».

Расчет критерия Шапиро и Уилка (W_набл) на ПЭВМ позволил установить, что:

.

Далее по таблице критических значений критерия Шапиро и Уилка (Приложение 3) ищем W_крит для n = 10. Находим, что W_крит = 0,842. Сравним величины W_крит и W_набл.

Делаем вывод: так как W_набл (0,839) < W_крит (0,842), должна быть принята конкурирующая гипотеза о распределении генеральной совокупности d_i, отличном от нормального. Поскольку выборки попарно зависимые, а распределение парных разностей отличается от нормального, для оценки эффективности применявшейся методики развития скоростных качеств следует использовать непараметрический U -критерий Уилкоксона.

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: