 |
Нормальный закон распределения результатов измерений
|
|
|
|
Многие ряды распределения, встречающиеся в статистических наблюдениях, можно охарактеризовать формулами разных математических функций. Функции или законы распределения случайных величин бывают: биноминальное, геометрическое, равномерное, нормальное и др. Самым важным в статистике является нормальное распределение.
Нормальное распределение – это совокупность объектов, в которой крайние значения некоторого признака – наименьшее и наибольшее – появляются редко; чем ближе значение признака к среднему значению, тем чаще оно встречается. Например, распределение студентов по их весу приближается к нормальному.
Нормальный закон (закон Гаусса) распределения результатов измерений непрерывных величин наиболее часто встречается и в спортивной практике.
Нормальное распределение описывается формулой, впервые предложенной английским математиком Муавром в 1733 году:
(5.1)
где p и e – математические константы (p = 3,141; e = 2,718); 
и s – соответственно, среднее арифметическое и среднее квадратическое отклонение результатов измерений; xi – результаты измерений; f(x) – так называемая функция плотности распределения.
Плотность распределения – это количество признака в единице интервала.
Формула (5.1) позволяет получить в виде графика кривую нормального распределения (рисунок 5.1), которая симметрична относительно центра группирования (как правило, это значение среднего арифметического ).
 |
Рисунок 5.1 – Кривая нормального распределения
Эта кривая может быть получена из полигона распределения при бесконечно большом числе наблюдений и интервалов (см. рисунок 2.1 II этапа игры).
Чтобы избежать неудобств, связанных с расчётами для каждого конкретного случая по достаточно сложной формуле (5.1), используют так называемое нормированное (или стандартное) нормальное распределение, для которого составлены подробные таблицы.
|
|
|
Нормированное нормальное распределение имеет параметры = 0 и σ = 1. Это распределение получается, если пронормировать нормально распределённую величину x по формуле:
.
Плотность распределения вероятностей нормированного нормального распределения записывается в виде:
.
На кривой нормированного нормального распределения (рисунок 5.2) указаны в процентах доли площадей, соответствующих отмеченным значениям нормированного отклонения u, по отношению к общей площади под кривой, равной 1 (100 %). Эти площади определяют вероятности попадания случайной величины в соответствующие интервалы.
Рисунок 5.2 – Кривая нормированного распределения
4. Основные свойства кривой нормального распределения (рисунок 5.1)
1. Кривая симметрична относительно среднего арифметического (моды, медианы).
2. При x = 
.
3. При 
.
4. Площадь, заключенная между кривой f(x) и осью x, равна единице.
5. Кривая имеет две точки перегиба при 
.
5. Влияние 
и σ на вид кривой нормального распределения
1. Изменение среднего арифметического значения не меняет форму кривой, а приводит лишь к сдвигу кривой вдоль оси X: 
при s = const.
 |
Рисунок 5.3 – Влияние на вид кривой нормального распределения
2. С увеличением s максимальная ордината кривой убывает, а сама кривая становится более пологой, при уменьшении s кривая становится более островершинной. При любых значениях и s площадь, ограниченная кривой и осью X, одинакова и равна единице.
В результате спортивной тренировки средняя арифметическая должна улучшаться (в зависимости от вида спорта или увеличиваться, или уменьшаться), а стандартное отклонение s должно уменьшаться. С увеличением стабильности и устойчивости спортивных результатов, составляющих нормально распределенные выборки, кривая распределения становится более островершинной.
|
|
|
Рисунок 5.4 – Влияние s на вид кривой нормального распределения
6. Вероятности попадания в области 
, 
, 
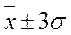. Правило трёх сигм
 |
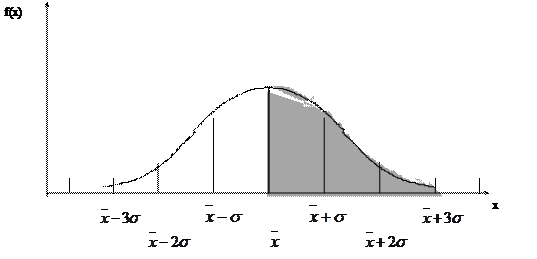Рисунок 5.5 – Вероятность попадания результатов, составляющих нормально распределенную выборку, на заданный участок кривой:
68,27 % всех результатов попадает на участок от 
до 
;
95,45 % всех результатов попадает на участок от 
до 
;
99,73 % всех результатов попадает на участок от 
до 
Правило трех сигм заключается в том, что практически все результаты, составляющие нормально распределенную выборку, находятся в пределах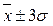 
.
Это правило можно использовать при решении следующих важных задач:
1. Оценки нормальности распределения выборочных данных. Если результаты находятся примерно в пределах 
и в области среднего арифметического результаты встречаются чаще, а вправо и влево от него – реже, то можно предположить, что результаты распределены нормально.
2. Выявление ошибочно полученных результатов. Если отдельные результаты отклоняются от среднего арифметического значения на величины, значительно превосходящие 3 s, нужно проверить правильность полученных величин. Часто такие «выскакивающие» результаты могут появиться в результате неисправности прибора, ошибки в измерении и расчетах.
3. Оценка величины s. Если размах варьирования R = Xmax – Xmin, разделить на 6, то мы получим грубо приближенное значение s.
Задавшись процентом попаданий P%, можно найти область
X ± u×s, где u – число сигм, согласно таблице 5.1:
Таблица 5.1 – Процентные точки нормированного нормального распределения
| P% | 99,9 | |||
| u | 1,64 | 1,96 | 2,58 | 3,29 |
|
|
|
