 |
Интервальные оценки параметров генеральной совокупности
|
|
|
|
Доверительный интервал. Доверительная вероятность
Под термином «оценка» понимаются как сами значения параметров генеральной совокупности, полученные по выборке, так и правило, по которому они получены. При формировании интервальных оценок определяют границы интервалов, между которыми с той или иной вероятностью находятся истинные значения параметров.
Вероятности, признанные достаточными для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик, называют доверительными.
В качестве доверительных вероятностей принято выбирать значения 0,9; 0,95; 0,99; 0,999 (их еще выражают в процентах).
(1 – α) – доверительная вероятность, а α – уровень значимости
(α = 0,1; 0,05; 0,01; 0,001), задающий вероятность того, что оцениваемый генеральный параметр выходит за границы доверительного интервала.
Выбор доверительной вероятности производится исследователем, исходя из практических соображений о той ответственности, с какой делаются выводы о генеральных параметрах. Как правило, в научных исследованиях в области спорта считается достаточной доверительная вероятность 0,95 (95 %).
Интервал, в котором с заданной доверительной вероятностью находится оцениваемый генеральный параметр, называется доверительным интервалом.
Иными словами, доверительным интервалом Jp называют случайный интервал (Q1, Q2), который накрывает неизвестную характеристику Q с доверительной вероятностью p.
 |
Границы доверительного интервала Jp называют:
Q1 = Q* - e1 – нижней доверительной границей;
Q2 = Q* + e2 – верхней доверительной границей.
Значения e1 и e2 могут совпадать (при симметричном распределении Q*) и быть разными (при несимметричном распределении Q*). Они характеризуют точность, а вероятность p – надежность определения Q. Между надежностью и точностью существует обратная зависимость: чем выше надежность, тем ниже точность определения Q и наоборот.
|
|
|
С увеличением числа измерений при заданном p повышается точность определения Q (уменьшаются e1 и e2).
Для точного расчета границ доверительного интервала необходимо знать закон распределения выборочной характеристики Q*.
Построение доверительного интервала для оценки среднего значения генеральной совокупности
Чтобы найти границы доверительного интервала для среднего значения генеральной совокупности необходимо выполнить следующие действия:
1) по полученной выборке объема n вычислить среднее арифметическое  и стандартную ошибку среднего арифметического
и стандартную ошибку среднего арифметического  по формуле:
по формуле:
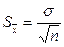 ;
;
2) задать доверительную вероятность 1 – α, исходя из цели исследования;
3) по таблице t -распределения Стьюдента (Приложение 4) найти граничное значение tα в зависимости от уровня значимости α и числа степеней свободы k = n – 1;
4) найти границы доверительного интервала по формуле:
 .
.
Примечание: В практике научных исследований, когда закон распределения малой выборочной совокупности (n < 30) неизвестен или отличен от нормального, пользуются вышеприведенной формулой для приближенной оценки доверительных интервалов.
Доверительный интервал при n ≥ 30 находится по следующей формуле:
 ,
,
где u a – процентные точки нормированного нормального распределения, которые находятся по таблице 5.1.
Порядок работы на V этапе
1. Проверить на нормальность распределения малую (n < 30) выборку, составленную из разностей парных значений результатов измерений исходного показателя скоростных качеств у «спортсменов» (эти результаты обозначены индексом В) и показателя, достигнутого после двухмесячных тренировок (эти результаты обозначены индексом Г).
|
|
|
2. Выбрать критерий и оценить эффективность метода тренировки, используемого для ускоренного развития скоростных качеств у «спортсменов».
3. Рассчитать и графически построить на числовой прямой доверительные интервалы генеральных средних арифметических выборок В и Г.
Отчет
о работе на V этапе игры
(образец)
Тема: Оценка эффективности методики тренировки.
Цели:
1. Ознакомиться с особенностями нормального закона распределения результатов тестирования.
2. Приобрести навыки по проверке выборочного распределения на нормальность.
3. Приобрести навыки оценки эффективности методики тренировки.
4. Научиться рассчитывать и строить доверительные интервалы для генеральных средних арифметических малых выборок.
Вопросы:
1. Сущность метода оценки эффективности методики тренировки.
2. Нормальный закон распределения. Сущность, значение.
3. Основные свойства кривой нормального распределения.
4. Правило трех сигм и его практическое применение.
5. Оценка нормальности распределения малой выборки.
6. Какие критерии и в каких случаях используются для сравнения средних попарно зависимых выборок?
7. Что характеризует доверительный интервал? Методика его определения.
Вариант 1: критерий параметрический
Примечание: В качестве примера возьмем приведенные в таблице 5.2 результаты измерения показателя скоростных качеств у спортсменов до начала тренировок (они обозначены индексом В, были получены в результате измерений на I этапе деловой игры) и после двух месяцев тренировок (они обозначены индексом Г).
От выборок В и Г перейдем к выборке, составленной из разностей парных значений di = NiГ – NiВ и определим квадраты этих разностей. Данные занесем в расчетную таблицу 5.2.
Таблица 5.2 – Расчет квадратов парных разностей значений di2
| № п/п | NiВ, уд | NiГ, уд | di = NiГ – NiВ, уд | di2, уд2 |
| -2 | ||||
| S = 50 | S = 484 |
Пользуясь таблицей 5.2, найдем среднее арифметическое парных разностей:
|
|
|
 уд.
уд.
Далее рассчитаем сумму квадратов отклонений di от  по формуле:
по формуле:
 уд.2
уд.2
Определим дисперсию для выборки di:
 уд.2
уд.2
Далее необходимо выборку, составленную из разностей парных значений di, проверить на нормальность распределения.
Выдвигаем гипотезы:
– нулевую – H0: о том, что генеральная совокупность парных разностей di имеет нормальное распределение;
– конкурирующую – H1: о том, что распределение генеральной совокупности парных разностей di отлично от нормального.
Проверку проводим на уровне значимости a = 0,05.
Для этого составим расчетную таблицу 5.3.
Таблица 5.3 – Данные расчета критерия Шапиро и Уилка Wнабл для выборки, составленной из разностей парных значений di
| № п/п | di, уд | k | dn - k + 1-dk=Dk | ank | Dk×ank |
| -2 | 17 – (–2) = 19 | 0,5739 | 10,9041 | ||
| 7 – 0 = 7 | 0,3291 | 2,3037 | |||
| 6 – 3 = 3 | 0,2141 | 0,6423 | |||
| 6 – 3 = 3 | 0,1224 | 0,3672 | |||
| 6 – 4 = 2 | 0,0399 | 0,0798 | |||
Порядок заполнения таблицы 5.3:
1. В первый столбец записываем номера по порядку.
2. Во второй – разности парных значений di в неубывающем порядке.
3. В третий – номера по порядку k парных разностей. Так как в нашем случае n = 10, то k изменяется от 1 до n /2 = 5.
4. В четвертый – разности Dk, которые находим таким образом:
– из самого большого значения d10 вычтем самое малое d1 и полученное значение запишем в строке для k = 1,
– из d9 вычтем d2 и полученное значение запишем в строке для k = 2 и т.д.
5. В пятый – записываем значения коэффициентов ank, взятые из таблицы, используемой в статистике для расчета критерия Шапиро и Уилка (W) проверки нормальности распределения (Приложение 2) для n = 10.
6. В шестой – произведение Dk × ank и находим сумму этих произведений:
 ;
;
 .
.
Наблюдаемое значение критерия Wнабл находим по формуле:
 .
.
Проверим правильность выполнения расчетов критерия Шапиро и Уилка (Wнабл) его расчетом на компьютере по программе «Статистика».
Расчет критерия Шапиро и Уилка (Wнабл) на компьютере позволил установить, что:
|
|
|
 .
.
Далее по таблице критических значений критерия Шапиро и Уилка (Приложение 3) ищем Wкрит для n = 10. Находим, что Wкрит = 0,842. Сравним величины Wкрит и Wнабл.
Делаем вывод: так как Wнабл (0,874) > Wкрит (0,842), должна быть принята нулевая гипотеза о нормальном распределении генеральной совокупности di. Следовательно, для оценки эффективности применявшейся методики развития скоростных качеств следует использовать параметрический t -критерий Стьюдента.
|
|
|


