Математические модели динамики возрастного состава стада

Попытаемся промоделировать те процессы, которые определяют изменения возрастной структуры стада. В основу анализа мною положены модели соотношения пополнения и убыли (Никольский, 1961а, 1963), запрограммированные и проанализированные В. В. Меншуткиным (1964а, 1965). Остановимся на их рассмотрении несколько подробнее.

Возьмем нерестовую популяцию с определенным распределением возрастов и допустим, что смертность ее особей неселективна и осуществляется с интенсивностью в 10 и 90% (табл. 61, 62 и рис. 37).

Рис. 37. Изменения среднего возраста популяции в зависимости от интенсивности вылова. Вылов 10 и 90%; смертность рыб старше 7 лет-100%; пополнение имеет постоянный возрастной состав: 3 года-20%; 4 года-60%; 5 лет-20% (по Никольскому, 1963)

Таблица 61. Влияние неселективной смертности нерестовой популяции на ее возрастную структуру (смертность-90%; смертность рыб старше 7+-100%; распределение пополнения: 3+-20%, 4+ -60%, 5+-20%)

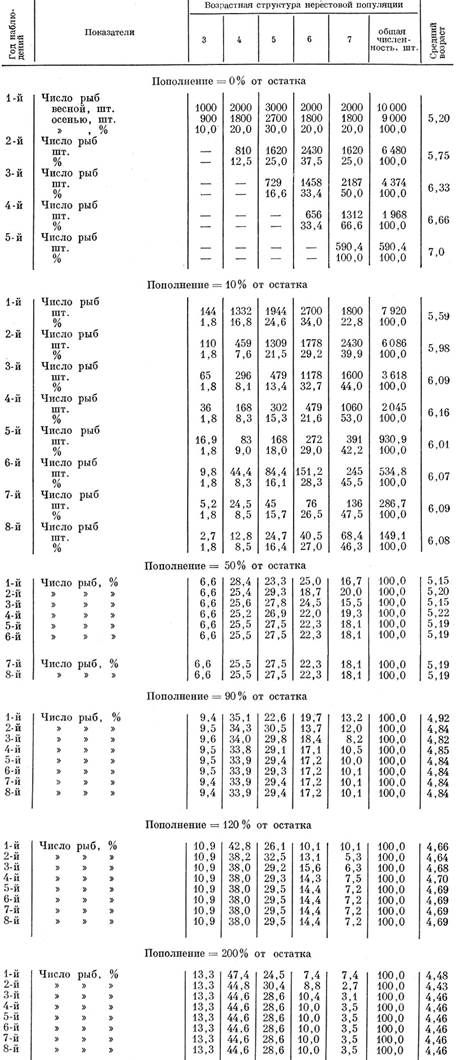
Таблица 62. Влияние неселективной смертности нерестовой популяции на ее возрастную структуру (смертность - 10%; смертность рыб старше 7+ -100%; распределение пополнения: 3 Г. -20%, 4 Г. -60%, 5 Г. -20%)

Естественно, что разовая неселективная гибель с любой интенсивностью, когда из каждой возрастной группы изымается такой же процент, какой она составляет в стаде, не меняет возрастной структуры стада.

8 первом примере исключим пополнение. На следующий год обе популяции при изъятии 10 и 90% сдвинутся на одну возрастную группу вправо, т. е. постареют на 1 год. Предельный возраст рыб в популяции - 7 лет. Это мы учитываем путем исключения из возрастного ряда рыб старше семилетнего возраста. При повторном изъятии такой же интенсивности повторится та же картина, и так будет продолжаться до тех пор, пока оставшиеся рыбы не достигнут предельного возраста и не погибнут от старости.

Проанализируем теперь, как будет изменяться возрастная структура нерестовой популяции при различной величине пополнения нерестового стада, причем примем, что возрастной состав пополнения (3-годовики - 20%; 4-годовики - 60; 5-годовики - 20%) остается неизменным. Исходная численность в случае изъятия 10 и 90% принята одинаковой, хотя это в данном случае не имеет практического значения. Расчет нами проведен для пополнения 10, 50, 90, 120 и 200% от остатка. Как видно из полученных данных, при одинаковой относительной величине пополнения и при изъятии 10 и 90% изменения возрастной структуры стада и среднего возраста популяции оказываются одинаковыми. До того момента (в наших моделях до пятилетнего возраста), пока в стаде остаются еще рыбы исходного ряда, наблюдаются некоторые колебания среднего возраста. Изменения среднего возраста в первые годы объясняются тем, какая по численности возрастная группа исходного ряда достигает предельного возраста и исключается из нерестового стада. Начиная же с момента, когда все стадо образуется уже ранее поступившими пополнениями, устанавливается стабильный средний возраст, одинаковый у популяций при изъятии и 10и 90% и не зависящий от абсолютной численности стада. Чем больший процент составляет пополнение по отношению к остатку, тем моложе оказывается средний возраст нерестовой популяции (рис. 38).

Рис. 38. Изменения возрастного состава промысловой популяции при изъятии 90 и 10% при различной величине пополнения (по Никольскому, 1963). Возрастной состав пополнения: 3-годовики - 20%; 4-годовики - 60%; 5-годовики - 20%; 1 - средний возраст популяции при вылове 90 и 10% и распределении пополнения: в первый год - 0%, во второй - 10%, в третий - 50%, в четвертый - 90%, в пятый - 120%; 2 - средний возраст популяции при вылове 90 и 10% и распределении пополнения: в первый год - 120%, во второй - 90%, в третий - 50%, в четвертый - 10%, в пятый - 0%

Мы попытались определить, как будет меняться возрастная структура нерестовой популяции, если ее численность остается стабильной. Такая стабильность достигается, если смертность составляет немногим более 43 %, а пополнение 100%. Ход изменений возрастного состава и среднего возраста популяции и в этом случае (табл. 63 и рис. 39) оказывается аналогичным тому, что наблюдается при вылове 10% и пополнении свыше 50%, когда численность популяции увеличивается, и при вылове 90%, когда численность популяции снижается.

Рис. 39. Изменение среднего возраста промысловых популяций при вылове 90 и 10 % и различном возрастном составе пополнения (по Никольскому, 1963). Возрастной состав пополнения непостоянен. Средний возраст пополнения: первый год - 3,9 г, второй - 3,7 г, третий - 3,4 г, четвертый - 3,2 г, пятый - 3,0 г

Таблица 63. Ход изменений возрастного состава и среднего возраста популяции при смертности 43% и пополнении 100% (возрастной состав пополнения тот же, что и в табл. 61 и 62). смертность рыб старше 7 лет - 100%

Проследим теперь, что произойдет, если интенсивность смертности будет увеличиваться из года в год, но соотношение пополнения и остатка будет оставаться прежним, т. е. пополнение будет составлять 50% от остатка при стабильном возрастном составе пополнения (табл. 64).

Таблица 64. Ход изменений возрастного состава и среднего возраста популяции при неизменном пополнении (50%) и распределении пополнения во всех случаях: 3-годовики - 20%; 4-годовики - 60%; 5-годовики - 20%

Как видно, никакого омоложения возрастного состава популяции не происходит. Средний возраст популяции остается примерно таким же, а небольшие колебания среднего возраста, как и в ранее рассмотренных случаях, связаны с тем, какая по мощности возрастная группа исходного ряда достигла предельного возраста и выбыла из состава стада.

Приведенные модельные примеры наглядно показывают, что неселективная смертность сама по себе не меняет структуры популяции. Изменения в возрастном составе популяции вызываются изменением величины и характера соотношения пополнения и остатка.

В табл. 65 и на см. рис. 38 и 39 показано, что произойдет в случае, если пополнение будет увеличиваться от 0% от остатка в первый год промысла до 120% на пятый год промысла. Как видно из приведенных цифр, в обоих случаях, и при вылове в 90%, и при вылове в 10%, и одинаковой возрастной структуре пополнения изменения, как возрастной структуры стада, так и среднего возраста будут сходны; при улучшении условий воспроизводства, т.е. увеличении процента пополнения по отношению к остатку, будет наблюдаться вне зависимости от интенсивности смертности омоложение стада.

Таблица 65. Ход изменений возрастного состава и среднего возраста популяции при распределении пополнения: в первый год - 0%, во второй год - 10%, в третий год - 50%, в четвертый год - 90%, в пятый год - 120% и соотношении отдельных возрастов в пополнении: 3-годовики - 20%, 4-годовики - 60%, 5-годовики - 20%

Обратная картина получается при прогрессирующем снижении относительной величины пополнения (табл. 66).

Таблица 66. Ход изменений возрастного состава и среднего возраста популяции при распределении пополнения: в первый год-120%, во второй год-90%, в третий год-50% в четвертый год-10%, в пятый год - 0% и соотношении возрастов в пополнении: 3-годовики - 20%, 4-годовики - 60% и 5-годовики - 20%

При уменьшении пополнения от 120 до 0% и при смертности 90 и 10% наблюдается сходная картина: постепенное увеличение среднего возраста облавливаемой популяции. Разная интенсивность смертности сама по себе и в этом случае не отражается на изменениях возрастной структуры популяции.

Посмотрим теперь, как будет изменяться возрастной состав нерестовой популяции при одной и той же интенсивности смертности (в нашем случае 10%), но при разной структуре пополнения. Как видно из табл. 67, при большем среднем возрасте пополнения происходит постарение стада, при меньшем - омоложение.

Таблица 67. Ход изменений возрастного состава и среднего возраста популяции при пополнении 90% и смертности 10%

Рассмотрим теперь такой случай, когда в результате ускорения роста особей в популяции происходит прогрессирующее омоложение возрастной структуры пополнения, которое меняется следующим образом (табл. 68).

Таблица 68. Условно принимаемая возрастная структура пополнения при ускорении роста особей в популяции

В итоге (убыль при расчете принята равной 10 и 90%) (см. табл. 66, 67 и 68) в зависимости от интенсивности пополнения средний возраст с большей или меньшей скоростью снижается, т. е. популяция омолаживается. При 10%-ном пополнении этот процесс идет значительно медленнее, чем при пополнении 90%.

Хотя приведенные примеры вычислены искусственно, нетрудно видеть, что для большинства из приведенных схем легко подобрать аналоги в природе. Например, данные см. табл. 61 и 62 отражают картину, очень напоминающую различные фазы динамики возрастного состава норвежской сельди, а данные табл. 69 и 70 - изменения, происходящие в стаде сельди Канала или у многих стад разных видов камбал.

Таблица 69. ход изменений возрастного состава и среднего возраста популяции при смертности 10 % и непостоянной структуре пополнения: 1-й год наблюдений: 3-годовики - 30 %, 4-годовики - 50 %, 5-годовики - 20 %; 2-й год наблюдений: 3-годовики - 40%, 4-годовики - 50 %, 5-годовики - 10 %; 3-й год наблюдений: 3-годовики - 60 %, 4-годовики - 40 %; 4-й год наблюдений: 3-годовики - 80 %, 4-годовики - 20 %; 5-й год наблюдений: 3-годовики - 100 %

Проведенный анализ позволяет сделать следующие общие выводы. Неселективная смертность любой интенсивности нерестовой популяции сама по себе еще не вызывает изменения возрастной структуры и среднего возраста стада. Омоложение возрастного состава стада может иметь место при: а) относительном увеличении процента пополнения по отношению к остатку и б) омоложении возрастной структуры пополнения. Наоборот, уменьшение процента пополнения по отношению к остатку и прогрессирующее увеличение среднего возраста пополнения приведут к увеличению среднего возраста нерестовой популяции. Таким образом, усиленный вылов молоди - неполовозрелых рыб - вызовет относительное сокращение пополнения и тем самым постарение нерестовой популяции.

П. В. Тюрин (1967) прав, подчеркивая, что при увеличении численности стада рыб следует ожидать уменьшения процента старших возрастных групп за счет высокой численности младших поколений. Наоборот, при сокращении численности стада за счет сокращения пополнения наблюдается повышение удельного веса старших возрастных групп в стаде. Омоложение стада далеко не всегда является результатом интенсивного вылова.

В приведенных выше моделях допущен ряд упрощений по сравнению с процессами, происходящими в естественных популяциях. Как известно, основное свойство популяций всех организмов, позволяющее им существовать многие тысячелетия в состоянии относительной стабильности, - это свойство саморегуляции в соответствии с обеспеченностью пищей.

На изменения соотношения пополнения и остатка популяция автоматически реагирует через изменение темпа роста половозрелых особей и их плодовитости изменением величины и структуры пополнения.

В приведенных выше моделях я искусственно отчленял один процесс от другого, в природе же они взаимосвязаны.

Таблица 70. ход изменений возрастной структуры и среднего возраста популяции при смертности 90% и изменяющейся структуре пополнения: 1-й год наблюдений: 3-годовики - 30 %, 4-годовики - 50 %, 5-годовики - 20 %; 2-й год наблюдений: 3-годовики - 40 %, 4-годовики - 50 %, 5-годовики - 10 %; 3-й год наблюдений: 3-годовики - 60 %, 4-годовики - 40 %; 4-й год наблюдений: 3-годовики - 80 %, 4-годовики - 20 %; 5-й год наблюдений: 3-годовики - 100 %

Схематически этот процесс в популяциях, у которых не нарушена система регуляторных связей со средой, рисуется в следующем виде: уменьшение численности нерестового стада в условиях стабильной кормовой базы приводит к увеличению относительной численности пополнения, что достигается повышением плодовитости оставшейся части стада вследствие ускорения темпа роста неполовозрелой части стада и более быстрого достижения половой зрелости. Кроме того, ранее созревшие особи раньше достигают предельного возраста и раньше гибнут от старости. Все эти процессы в их взаимодействии несложно изобразить в виде математической модели, в основу которой положен тот же принцип, что и в рассмотренных ранее (табл. 71).

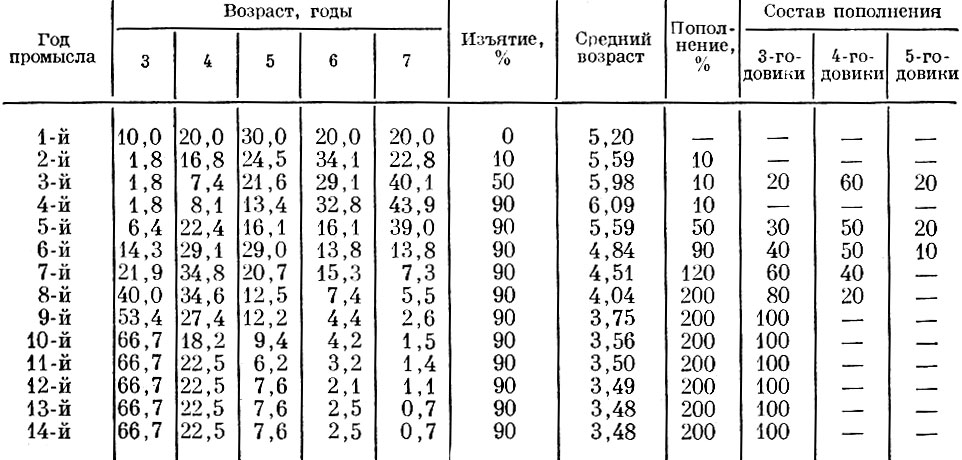
Таблица 71. Модель динамики популяции с регуляторными механизмами (изменение возрастного состава и процента пополнения) и запаздыванием реакции на три года (возраст половой зрелости). смертность рыб старше 7 лет - 100 %

В этой модели (см. табл. 71) мы имеем случай, когда смертность популяции возрастает, пополнение с опозданием на три года (возраст достижения половой зрелости) тоже возрастает и происходит омоложение возраст-но го ряда пополнения.

Темп этих процессов принят тот же, что и в ранее рассмотренных моделях, а сокращение продолжительности жизни пропорционально сдвигу в возрасте достижения половой зрелости. Мы не включали в модель того, что у части особей, созревающих ранее, несколько уменьшается естественная продолжительность жизни, хотя это также очень просто промоделировать. Ход процесса при этом изменится очень незначительно.

Исходная численность популяции на четвертый квартал первого года 10 000 шт., численное соотношение отдельных возрастных групп в стаде: 3-годовики - 1000, 4-годовики - 2000, 5-годовики - 3000, 6-го-довики - 2000, 7-годовики - 2000.

На второй год в первом квартале возраст соответственных возрастных групп увеличивается на 1 год и полностью отмирают 8-летние особи. Численность популяции равняется 10000 шт., численность 7-годовиков, ставших 8-годовиками, будет 10000-2000 = 8000.

К началу второго квартала второго года нерестовая популяция получает пополнение в составе 10% от ее численности (от 8000); возрастной состав пополнения: 3-годовики - 20%, 4-годовики - 60%, 5-годовики - 20%.

Во втором и третьем кварталах второго года происходит изъятие части (10%) нерестовой популяции. Таким образом, численность популяции становится (8000 + 10% от 8000) 9:10 = 7920 экз.

На третий год в первом квартале возраст соответственных возрастных групп увеличивается на 1 год и отмирают 8-годовики. В дальнейшем по этому принципу в связи с заданными параметрами меняются численность, возрастной состав и средний возраст нерестовой популяции.

Во второй, третий и четвертый годы при стабильном и малочисленном пополнении (10%) средний возраст рыб в популяции увеличивается и при постоянно растущем проценте изъятия (от 10 до 90) резко сокращается ее численность. В последующие годы при постоянном проценте изъятия (90) численность нерестовой популяции продолжает уменьшаться.

С пятого по девятый год наблюдений, когда созревает пополнение годов с повышенным изъятием, увеличивается относительная численность ежегодного пополнения нерестовой популяции (с 10 до 200%) и изменяется его возрастной состав (средний возраст пополнения уменьшается).

Действие этих двух факторов приводит к изменению возрастного состава и среднего возраста популяции. Средний возраст рыб в популяции уменьшается довольно резко - с 6,09 до 3,75.

В последующие 5 лет (10-14-й годы наблюдений) изъятие, пополнение в его возрастной состав стабильны. По мере увеличения возраста и отмирания старших поколений уменьшается (более постепенно) средний возраст популяции, и с 13-го года возрастной состав популяции стабилизируется. Это означает, что поколения, составлявшие нерестовую популяцию до стабилизации исходных параметров, полностью заменились более молодыми. Соотношения численностей этих последующих поколений полностью диктуются исходными параметрами (считая с десятого года наблюдений). Начиная с девятого года наблюдений, популяция доведена до такого состояния, когда ее регуляторные механизмы перестают реагировать на изменения обеспеченности пищей. Мы не приводим здесь модели, в которой процессы идут в обратном направлении, т. е. смертность снижается, темп роста замедляется и связанная с ним структура пополнения меняется - пополнение происходит в более позднем возрасте.

В моделях этого типа устранен недостаток первых двух типов: в них включен комплекс регуляторных механизмов (естественно, не все), который делает эти модели еще более близкими к действительности. Рассмотренный тип модели был изучен на электронно-вычислительной машине В. В. Меншуткиным (1965).

Конечно, в большинстве случаев промысел носит селективный характер, отбирая из стада более крупных рыб или рыб какого-нибудь одного пола. Но во многих случаях, особенно при облове нерестовых популяций, промысел не селективен (например, лов ходовых лососей заездками или ходовой воблы неводами) и в улове рыбы разного размера и возраста содержатся в том же соотношении, что и в облавливаемой нерестовой популяции. Поправка на селективность всегда может быть введена в модель.

Как это хорошо показал еще Г. Н. Монастырский (1940) на примере северокаспийской воблы, мы можем, зная возрастной состав уловов, темп роста, относительную численность пополнения, легко промоделировать процесс перестройки структуры популяции, а тем самым по биологическим показателям, характеризующим популяцию, оценить и изменения ее численности и биомассы.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: