Количество воспроизведенных слов

№ испытуемого	Низкая скорость	Средняя скорость	Высокая скорость

№ 11.4. Группа из 5 испытуемых была обследована с помощью трех экспериментальных заданий, направленных на изучение интеллектуальной настойчивости (Сидоренко Е.В., 1984). Каждому испытуемому индивидуально предъявлялись три одинаковые анаграммы: четырехбуквенная, пятибуквенная и шестибуквенная.

Длительность попыток решения анаграмм (сек)

Код испытуемого	4-буквенная анаграмма	5-буквенная анаграмма	6-буквенная анаграмма

 

Можно ли считать, что фактор длины анаграммы влияет на длительность попыток ее решения?

 

№ 11.5. В исследовании Cиэрс (1940) (Гласс, Стенли) детям давались обычные арифметические задачи, а затем одной случайно выбранной половине сообщалось, что они не выдержали испытания, а остальным – обратное. Затем у каждого ребенка спрашивали, сколько секунд ему потребовалось бы для решения новой задачи. Экспериментатор вычислял разность между ожидаемым временем решения задачи (в сек), которое называл ребенок, и результатом ранее выполненного задания. Полагали, что провалившиеся на предыдущем испытании могли проявить некоторую неуверенность при оценке своих намерений.

Проверяемая на уровне значимости р=0,05 гипотеза состоит в том, что дисперсия совокупности детских оценок, имеющих отношение к оценке их возможностей, постоянна независимо от того, сообщалось детям о плохих результатах испытаний или об удачном решении первой задачи. Сиэрс получила следующие данные:

 

Учащиеся, которым сообщалось о положительном результате	Учащиеся, которым сообщалось о неудаче
N1 = 12	N2 = 12
S2= 8,16	S2 = 90,45

 

№ 11.6. Изучалось образование условного рефлекса у собаки под действием некоторого ранее индифферентного раздражителя. Количественным признаком служило время (в сек.) между моментом включения условного раздражителя и моментом начала слюноотделения. Исследование было поставлено на пяти собаках, причем на каждой проделано шесть опытов. Результаты представлены в таблице.

 

Номера собак	Результаты опытов

Для повышения точности общего результата следует увеличить число подопытных животных или следует увеличить число опытов на каждом из них?

 

№ 11.7. Из совокупности 2500 десятых классов, изучающих геометрию, для участия в эксперименте было выбрано случайным образом 48 классов. Исследователь хотел оценить эффективность 2 различных методов и окружающих условий в процессе изучения геометрии, а также определить их взаимодействия. Случайным образом классы приписывались в равных количествах четырем комбинациям окружающих условий и методов. По окончании одного семестра исследователь провел одну и ту же контрольную работу по геометрии в каждом классе. Так как выборочным элементом является «класс», то в качестве элемента анализа рассматривается средний класс (округленный до ближайшего целого) по критерию успеваемости. Результаты представлены в таблице.

 

	Фактор В, условия
Лекция в классе (1)	Программированное обучение (2)
Фактор А, методы	Традиционные (1)	2, 5, 6, 7, 4, 6, 7, 8, 4, 6, 7, 10	9, 12, 14, 15, 10, 13, 14, 16, 10, 13, 14, 17
Современные (2)	10, 13, 14, 16, 10, 13, 14, 17, 11, 13, 15, 17	21, 25, 31, 33, 22, 26, 32, 34, 22, 30, 32, 35

 

№ 11.8. Сравнить три варианта метода преподавания (А.В.С), которые отличаются всего одним признаком – применением наглядного материала. Был проведен эксперимент, состоящий в том, что каждому из трех равных по объему случайных контингентов учеников из параллельных классов преподавание определенного учебного материала осуществлялось только по одному из указанных вариантов. В заключение была проведена контрольная работа, результаты которой оценивались в баллах. Первичные данные эксперимента представлены в таблице.

Определить: А) Однородны ли дисперсии оценок, полученных учениками, обучение которых проводилось с различным использованием наглядного материала, для критерия Кохрана G_0,05=0,547.

Б) Одинаково ли эффективны эти три метода преподавания.

 

Метод А	Метод В	Метод С
Оценки в баллах

№ 11.9. Определить влияют ли метод преподавания и предыдущая успеваемость ученика на успешность усвоения нового материала. Пусть первый фактор (А) – это наглядность в преподавании; он имеет три уровня. Второй фактор (В) – это предыдущая успеваемость школьников; пусть он имеет по-прежнему пятнадцать уровней.

 

	Уровни А
А1	А2	А3
Уровни В	В1
В2
В3
В4
В5
В6
В7
В8
В9
В10
В11
В12
В13
В14
В15

 

№ 11.10. Влияет ли семейное положение на свободное время (в часах), проводимое не дома. Обусловлено ли время, проводимое вне дома семейным положением и полом? (А.Д.Резник).

 

Пол	№ п/п	Свободное время (в часах), проводимое не дома
холостые	женатые	разведенные
мужчины
женщины

 

№ 11.11. Экспериментально исследовалось влияние двух факторов на успешность прохождения крысами лабиринта. Один из факторов – степень подвижности (активности) крысы, другой – условия воспитания, в различной мере способствующие формированию активности животного. Было три уровня первого фактора, по которым все крысы подразделялись на три группы: подвижных, уравновешенных и вялых, и два уровня второго фактора, по которым каждая из трех групп делилась на две подгруппы: воспитывающиеся в свободных условиях и воспитывающихся в стесненных условиях. В каждую из подгрупп (блоков) входило восемь крыс. Определить значимость факторов на успешность выполнения задания.

 

	k	Степень активности крысы (Аj)
А1 -подвижные	А2- уравновешенные	А3- вялые
Условия воспитания   Bj	Свободные В1
Стесненные В2

12. ФАКТОРНЫЙ АНАЛИЗ

Факторный анализ – комплекс аналитических методов, позволяющих выявить скрытые (латентные) признаки, а также причины их возникновения и внутренние закономерности их взаимосвязи. Главная цель факторного анализа – уменьшение размерности описания исходных данных при условии минимальных потерь исходной информации.

Основные задачи факторного анализа

1. Исследование структуры взаимосвязей переменных. В этом случае каждая группировка переменных будет определяться фактором, по которому эти переменные имеют максимальные нагрузки.

2. Идентификация факторов как скрытых (латентных) переменных– причин взаимосвязи исходных переменных.

3. Вычисление значений факторов для испытуемых как новых, интегральных переменных. При этом число факторов существенно меньше числа исходных переменных. В этом смысле факторный анализ решает задачу сокращения количества признаков с минимальными потерями исходной информации.

Исходной информацией для проведения факторного анализа является корреляционная матрица, или матрица интерколяций показателей тестов.

Проблема числа факторов.

Для определения числа факторов были предложены критерии Кайзера-Гуттмана и критерий отсеивания Р.Кеттелла.

Критерий Кайзера: число факторов равно числу компонент, собственные значения которых больше 1 (Eigenvalue, λ>1).

Критерий отсеивания Р.Кеттелла (scree-test), требует построения графика собственных значений. Количество факторов определяется приблизительно по точке перегиба на графике собственных значений до его выхода на пологую прямую после резкого спада. При этом проверяется три гипотезы: если К – точка перегиба, то возможное количество факторов равно К-1, К и К+1.

Окончательное решение о числе факторов принимается после интерпретации факторов.

Проблема общности.

Единичная дисперсия каждой переменной может быть представлена в факторном анализе как сумма ее общности и характерности:

1=h_i²+e_i²,

где h_i²- общность переменной с номером i; e_i² – ее характерность.

Общность – это часть дисперсии переменной, обусловленная действием общих факторов. Общность - показатель участия переменной в факторном анализе, насколько она влияет на факторную структуру.

Переменная с большей общностью имеет значительную степень перекрытия (большую долю дисперсии) с одним или несколькими факторами. Низкая общность подразумевает, что все корреляции между переменными и факторами невелики.

Общность переменной i равна сумме квадратов ее нагрузок по всем М факторам (по строке факторных нагрузок):

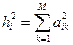
Характерность - часть ее дисперсии, обусловленная спецификой данной переменной и ошибками измерения.

Различия в методах факторного анализа определяются тем, как решается проблема общностей.

Методы факторного анализа – различные способы получения факторной структуры при заданном числе факторов. Наиболее распространенные: анализ главных компонент, метод главных осей, факторный анализ образов, метод не взвешенных наименьших квадратов, обобщенный метод наименьших квадратов, метод максимального правдоподобия.

Анализ главных компонент преобразует набор коррелирующих переменных в другой набор – некоррелирующих переменных.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: