 |
Операции над множествами и их свойства.
|
|
|
|
О.В. Собенина
ДИСКРЕТНАЯ МАТЕМАТИКА
Учебное пособие

Воронеж 2012
ФГБОУ ВПО «Воронежский государственный технический университет»
О.В. Собенина
ДИСКРЕТНАЯ МАТЕМАТИКА
Утверждено Редакционно-издательским советом университета
В качестве учебного пособия
Воронеж 2012
УДК 519.1
Собенина О.В. Дискретная математика: учеб. пособие / О.В. Собенина. Воронеж: ФГБОУ ВПО «Воронежский государственный технический университет», 2012. 196 с.
В учебном пособии излагаются основы современной дискретной математики: теория множеств, бинарные отношения, теория графов, алгебра высказываний. Каждый раздел иллюстрирован примерами, содержит задачи и упражнения для развития навыков решения основных типов задач.
Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлению 230100.62 «Информатика и вычислительная техника» (профиль «Системы автоматизированного проектирования в машиностроении»), дисциплине «Дискретная математика».
Учебное пособие подготовлено в электронном виде в текстовом редакторе Word и содержится в файле «diskret.doc».
Библиогр.: 10 назв.
| Рецензенты: | кафедра вычислительной математики и прикладных информационных технологий Воронежского государственного университета (зав. кафедрой д-р техн. наук, проф. Т.М. Леденева); канд. физ.-мат. наук, доц. В.Н. Дурова |
Ó Собенина О.В., 2012
Ó Оформление. ФГБОУ ВПО
«Воронежский государственный
технический университет», 2012
ВВЕДЕНИЕ
Дискретная математика – область математики, занимающаяся изучением свойств дискретных структур, которые возникают как внутри математики, так и в ее приложениях. Дискретность (от лат discretus – разделенный, прерывистый) – прерывность; противопоставляется непрерывности. Например, система целых чисел (в противоположность системе действительных чисел) является дискретной; дискретное изучение какой-либо величины во времени – это изменение, происходящее через определенные промежутки времени (скачками).
|
|
|
В отличие от дискретной математики классическая математика в основном занимается изучением свойств объектов непрерывного характера. Использование классической математики или дискретной математики как аппаратов исследования связано с тем, какие задачи ставит перед собой исследователь, и в связи с этим, какую модель изучаемого явления он рассматривает: дискретную или непрерывную.
Дискретная математика представляет собой важное направление в математике, в котором можно выделить характерные для дискретной математики предметы исследования, методы и задачи, специфика которых обусловлена в первую очередь необходимостью отказа в дискретной математике от основополагающих понятий классической математики – предела и непрерывности. В связи с этим для многих задач дискретной математики сильные средства классической математики оказываются, как правило, малоприемлемыми.
Элементы дискретной математики возникли в глубокой древности. Развиваясь с другими разделами математики, они явились их составной частью. Типичными для того времени были задачи, связанные со свойствами целых чисел и приведшие затем к созданию теории чисел. К их числу могут быть отнесены отыскания алгоритмов сложения и умножения натуральных чисел (2-е тыс. до н. э.), задачи о суммировании и вопросы делимости натуральных чисел в пифагорейской школе (6 в. до н. э.) и т.д.
Стремление к строгости математических рассуждений и анализ рабочего инструмента математики – логики – привели к выделению еще одного важного раздела математики – математической логики (19-20 вв.).
|
|
|
Однако наибольшего развития дискретная математика достигла в связи с запросами практики, приведшими к появлению новой науки – кибернетики и ее теоретической части – математической кибернетики (20 в.)
Дискретная математика включает в себя такие математические разделы, как теория множеств и отношений, теория графов, теория алгоритмов, комбинаторный анализ, математическую логику и другие, которые наиболее интенсивно стали развиваться в связи с внедрением вычислительной техники. Теория графов является эффективным аппаратом формализации современных инженерных задач, связанных с дискретными объектами. Такие задачи возникают при проектировании интегральных схем и схем управления, при исследовании автоматов и логических цепей, при системном анализе, автоматизированном управлении производством и дискретной оптимизации. Широкое применение дискретная математика нашла в современной вычислительной технике: в теоретическом программировании, при проектировании ЭВМ и сетей ЭВМ, баз данных, систем логического управления. Элементы математической логики применяются при решении проблем функционально-логического проектирования.
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
1.1. Основные понятия и определения теории множеств
Любое понятие дискретной математики можно определить с помощью понятия множества, которое является одним из фундаментальных понятий и было сформулировано впервые немецким математиком Г. Кантором.
Под множеством понимается любая совокупность определенных и различимых между собой объектов, мыслимая как единое целое.
Можно говорить о множестве стульев в комнате, людей, живущих в г. Воронеже, студентов в группе, о множестве натуральных чисел, букв в алфавите, состояний системы и т. п. При этом о множестве можно вести речь только тогда, когда элементы множества различимы между собой. Например, нельзя говорить о множестве капель в стакане воды, так как невозможно четко и ясно указать каждую отдельную каплю.
Отдельные объекты, из которых состоит множество, называют элементами множества. Так, число 3 – элемент множества натуральных чисел, а буква б – элемент множества букв русского алфавита.
|
|
|
Общим обозначением множества служит пара фигурных скобок { }, внутри которых перечисляются элементы множества. Для обозначения конкретных множеств используют различные прописные буквы A, S, X... или прописные буквы с индексами А 1, А 2. Для обозначения элементов множества в общем виде используют различные строчные буквы а, s, x... или строчные буквы с индексами а 1, а 2...
Для указания того, что некоторый элемент а является элементом множества S, используется символ Î принадлежности множеству. Запись a Î S означает, что элемент a принадлежит множеству S, а запись x Ï S означает, что элемент х не принадлежит множеству S. Записью х 1, x 2,......, xn Î S пользуются в качестве сокращения для записи x 1Î S, x 2Î S,..., xn Î S.
Как правило, считается, что все элементы множества различны. Множество с повторяющимися элементами называется мультимножеством. Мультимножества играют важную роль в комбинаторике. В дальнейшем будут рассматриваться множества с различными элементами.
Будем использовать следующие обозначения для числовых множеств:
 – множество натуральных чисел, т.е.
– множество натуральных чисел, т.е. 
 – множество целых чисел, т.е.
– множество целых чисел, т.е.  = {0, ±1, ±2, …};
= {0, ±1, ±2, …};
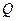 – множество рациональных чисел,
– множество рациональных чисел, 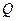 ={
={  /
/  \
\  ,
,  Î
Î  ;
;  ¹ 0};
¹ 0};
 – множество вещественных чисел;
– множество вещественных чисел;
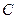 – множество комплексных чисел.
– множество комплексных чисел.
Множества бывают конечными и бесконечными. Множество называют конечным, если число его элементов конечно, т. е. если существует натуральное число n, являющееся числом элементов множества. Множество называют бесконечным, если оно содержит бесконечное число элементов. Количество элементов конечного множества называется мощностью и обозначается  = n, если множество X содержит n элементов.
= n, если множество X содержит n элементов.
Важным понятием теории множеств является понятие пустого множества. Пустым множеством называют множество, не содержащее ни одного элемента. Пустое множествообозначают символом  Например:
Например:
{ x Î R | x 2- x +1=0}= 
Понятие пустого множества играет очень важную роль при задании множеств с помощью описания. Так, без понятия пустого множества мы не могли бы говорить о множестве отличников группы или о множестве вещественных корней квадратного уравнения, не убедившись предварительно, есть ли вообще в данной группе отличники или имеет ли данное уравнение вещественные корни. Введение пустого множества позволяет совершенно спокойно оперировать с множеством отличников группы, не заботясь о том, есть или нет в рассматриваемой группе отличники. Пустое множество будем условно относить к конечным множествам.
|
|
|
Множество, содержащие все элементы, находящиеся в рассмотрении, называется универсальным или универсумом и обозначается U.
Для того чтобы оперировать с конкретными множествами, нужно уметь их задавать. Существуют два способа задания множеств: перечисление и описание. Задание множества способом перечисления соответствует перечислению всех элементов, составляющих множество. Так, множество отличников группы можно задать, перечислив студентов, которые учатся на отлично, например {Иванов, Петров, Сидоров}. Для сокращения записи Х ={ х 1, х 2,..., хn } иногда вводят множество индексов I ={1, 2,..., n } и пишут X ={ xi }, i Î I. Такой способ удобен при рассмотрении конечных множеств, содержащих небольшое число элементов, но иногда он может применяться и для задания бесконечных множеств, например {2, 4, 6, 8...}. Естественно, что такая запись применима, если вполне ясно, что понимается под многоточием.
Описательный способ задания множества состоит в том, что указывается характерное свойство, которым обладают все элементы множества. При этом используется запись
X ={ x | x обладает свойством Q (x)}.
Выражение в скобках читается: множество всех элементов х, которые обладают свойством Q (x). Так, если М — множество студентов группы, то множество A отличников этой группы запишется в виде А ={ х Î М | х – отличник группы},
что читается следующим образом: множество А состоит из элементов х множества М, обладающих тем свойством, что х является отличником группы.
В тех случаях, когда не вызывает сомнений, из какого множества берутся элементы х, указание о принадлежности х множеству М можно не делать. При этом множество А запишется в виде
А={ х | х – отличник группы}.
Приведем несколько примеров задания множеств методом описания: { x | x – четное} – множество четных чисел;
{ х | х 2–1=0} – множество {+1, –1}.
Пусть Z – множество целых чисел. Тогда { x Î Z | 0< x £7} есть множество {1, 2, 3, 4, 5, 6, 7}.
Множество нечетных чисел можно определить как { x | x =2 k +1 для некоторого k Î Z }.
|
|
|
Способ задания множества с помощью свойств таит некоторые опасности, поскольку «неправильно» заданные свойства могут привести к противоречию. Приведем один из наиболее типичных парадоксов – парадокс Рассела. Рассмотрим множество всех множеств, которые не являются своими собственными элементами:  . Спросим теперь, является ли множества К своим элементом? Если К Î К, то должно выполняться свойство, задающее множество К, т.е. К Ï К, что приводит к противоречию. Если К Ï К, то, поскольку выполняется свойство, задающее К, приходим к тому, что К Î К, а это противоречит предположению. Таким образом, не всякое свойство приводит к осмысленному заданию множества.
. Спросим теперь, является ли множества К своим элементом? Если К Î К, то должно выполняться свойство, задающее множество К, т.е. К Ï К, что приводит к противоречию. Если К Ï К, то, поскольку выполняется свойство, задающее К, приходим к тому, что К Î К, а это противоречит предположению. Таким образом, не всякое свойство приводит к осмысленному заданию множества.
Кроме того, множество можно задать с помощью характеристической функции, значения которой указывают является ли (да или нет) х элементом множества Х:
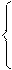



Заметим, что для любых элементов  = 0;
= 0; 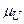 = 1.
= 1.
Пример. Пусть на универсуме U ={ a,b,c,d,e } определено множество X ={ a,c,d }, тогда

Для произвольных множеств X и Y можно определить два типа отношений – отношение равенства и отношение включения.
Два множества считаются равными, если они состоят из одних и тех же элементов. Принято обозначение X = Y, если X и Y равны, и X  Y – иначе.
Y – иначе.
Легко видеть, что для любых множеств X, Y, Z справедливы соотношения
 ,
,
 ,
,
( и
и  )
)  .
.
Из определения равенства множеств вытекает, что порядок элементов в множестве несуществен. Так, например, множества {3, 4, 5, 6} и {4, 5, 6, 3} представляют собой одно и то же множество.
Если каждый элемент множества X является элементом множества Y, то говорят, что X включено в Y и обозначают 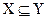 :
:
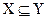
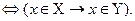
В этом случае говорят, что множество X является подмножеством множества Y. В частности X и Y могут совпадать, поэтому  называется также отношением нестрогого включения. Отметим некоторые свойства подмножества, вытекающее из его определения:
называется также отношением нестрогого включения. Отметим некоторые свойства подмножества, вытекающее из его определения:
 ,
,
(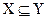 и
и  .
.
Если 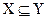 и
и  , то говорят, что X есть собственное подмножество Y и обозначают
, то говорят, что X есть собственное подмножество Y и обозначают 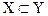 , отношение между множествами в этом случае называется отношением нестрогого включения. Для отношения строгого включения справедливо
, отношение между множествами в этом случае называется отношением нестрогого включения. Для отношения строгого включения справедливо
(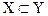 и
и  .
.
Невключение подмножества X в множество Y обозначается 
Пример. Пусть Y — множество студентов группы, а Х – множество отличников той же группы. Так как каждый отличник группы является в то же время студентом этой группы, то множество X является подмножеством множества Y.
Замечание. Не следует смешивать отношение принадлежности Î и отношение включения  . Хотя
. Хотя  и
и  , неверно, что
, неверно, что  , поскольку единственным элементом множества
, поскольку единственным элементом множества  является {0}.
является {0}.
Пример. Справедливы следующие включения: N Ì Z, Z Ì Q, Q Ì R, R Ì C.
Заметим, что если X является подмножеством Y и наоборот, то X и Y состоят из одних и тех же элементов, поэтому
 и
и 
Таким образом, чтобы доказать равенство двух множеств, надо установить два включения.
Пример. Покажем, что множества М1 ={ x | sin x = 1} и M2 ={ x | x =  ,
, 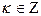 } совпадают.
} совпадают.
Если x  М1, то x является решением уравнения sin x =1. Но это значит, что x можно представить в виде x =
М1, то x является решением уравнения sin x =1. Но это значит, что x можно представить в виде x =  и поэтому x
и поэтому x  М2. Таким образом,
М2. Таким образом,  . Если x
. Если x  М2 , т.е. x =
М2 , т.е. x =  , то sin x =1, т.е.
, то sin x =1, т.е. 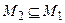 . Следовательно, М1 = М2.
. Следовательно, М1 = М2.
Для каждого множества X существует множество, элементами которого являются различные подмножества множества X. Такое множество называется семейством множества или булеаном множества X и обозначается P (X) Так как  включено в любое множество, то
включено в любое множество, то  .
.
Пример. Пусть 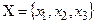 . Тогда
. Тогда

Операции над множествами и их свойства.
Диаграммы Эйлера-Венна
Для получения новых множеств из уже существующих используют операции над множествами. Рассмотрим основные из них.
Объединением множеств X и Y называется множество  , все элементы которого являются элементами множества X или Y:
, все элементы которого являются элементами множества X или Y:
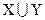 ={ x
={ x  x
x  или
или  }.
}.
Пересечением множеств X и Y называется множество  , элементы которого являются элементами обоих множеств X и Y:
, элементы которого являются элементами обоих множеств X и Y:
 ={ x | x
={ x | x  X и x
X и x  Y}.
Y}.
Очевидно, что выполняются включения

 ;
; 

Разностью множеств X и Y называется множество  всех тех элементов X, которые не принадлежат Y:
всех тех элементов X, которые не принадлежат Y:
 ={ x
={ x  x
x  и
и 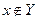 }.
}.
Дополнением множества X называется множество  всех тех элементов x, которые не принадлежат множеству X:
всех тех элементов x, которые не принадлежат множеству X:
 .
.
Симметрической разностью (или кольцевой суммой) множеств X и Y называется множество
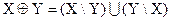 .
.
Замечание.  .
.
Универсальное множество графически изображают в виде множества точек прямоугольника, отдельные области внутри этого прямоугольника соответствуют различным подмножествам универсального множества. Такое представление универсального множества и его подмножеств называется диаграммой Эйлера-Венна. На диаграмме Эйлера-Венна можно проиллюстрировать все основные операции над множествами (рис. 1.1-1.5).

Операции над множествами обладают определенными свойствами и удовлетворяют некоторым соотношениям. Рассмотрим следующие утверждения.
Утверждение 1.2.1. Для любых множеств X, Y, Z выполняются следующие тождества (основные свойства операций):
1. Коммутативность операций 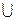 и
и  :
:

2. Ассоциативность операций  и
и  :
:


3. Законы дистрибутивности


4.  .
.
5.  .
.
6. Законы комплиментарности: 

7. Законы идемпотентности: 
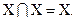
8. Законы де Моргана: 
 .
.
(Август де Морган (1806–1871) – английский математик).
9. Закон двойного дополнения 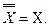
10. Законы поглощения


Докажем один из законной дистрибутивности:

Доказательство. Чтобы доказать равенство двух множеств А = В нужно доказать, что А Í В и В Í А. Докажем, что 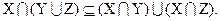 Для доказательства этого включения выберем произвольный элемент из множества
Для доказательства этого включения выберем произвольный элемент из множества  и покажем, что он принадлежит множеству
и покажем, что он принадлежит множеству  . Итак, пусть
. Итак, пусть  . Тогда
. Тогда  и
и  . Если
. Если  , то
, то  , а значит,
, а значит,  . Если
. Если 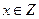 , то
, то  , а значит,
, а значит,  . Таким образом,
. Таким образом,
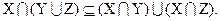
Теперь докажем, что  Пусть
Пусть  . Если
. Если  , то
, то  и
и  , отсюда следует, что
, отсюда следует, что  и
и  , т.е.
, т.е.  . Если
. Если  , то
, то  и
и 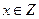 . Отсюда следует, что
. Отсюда следует, что  и
и  , т.е.
, т.е.  . Итак,
. Итак,  Таким образом, получили, что
Таким образом, получили, что  и
и  ,
,
а это значит, что эти два множества равны.
Доказательство можно оформить в более формализованном виде, используя “{” для системы высказываний, объединенных союзом “и”, “[”- для системы высказываний, объединенных союзом «или».
Докажем, один из законов де Моргана:  .
.
С одной стороны,

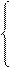

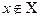







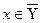

 .
.
С другой стороны,




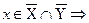

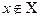





Так как  и
и  , то
, то  , что и требовалось доказать.
, что и требовалось доказать.
Утверждение 1.2.2.Следующие предложения о произвольных множествах попарно эквивалентны:
1)  ; 2)
; 2) 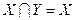 ; 3)
; 3)  ; 4)
; 4) 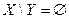 ; 5)
; 5)  .
.
Доказательство. 1  2. Так как
2. Так как  , то достаточно показать, что
, то достаточно показать, что  влечет
влечет  . Но если
. Но если  , то по условию
, то по условию  , и, следовательно,
, и, следовательно,  .
.
2  3. Так как
3. Так как  , то
, то  . По закону поглощения и закону коммутативности имеем
. По закону поглощения и закону коммутативности имеем 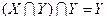 . Тогда
. Тогда  .
.
3  4. Предположим, что
4. Предположим, что  . Так как
. Так как  , то по закону де Моргана, закону ассоциативности, закону коммутативности, закону комплиментарности и закону 4 имеем
, то по закону де Моргана, закону ассоциативности, закону коммутативности, закону комплиментарности и закону 4 имеем
 .
.
4  5. Предположим, что
5. Предположим, что  , т. е.
, т. е.  . Тогда
. Тогда  . По закону де Моргана и закону двойного отрицания получаем
. По закону де Моргана и закону двойного отрицания получаем  .
.
5  1. Предположим, что
1. Предположим, что  и не выполняется условие
и не выполняется условие  , т. е. найдется элемент x такой, что
, т. е. найдется элемент x такой, что  и
и 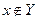 . Тогда
. Тогда 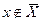 и, значит,
и, значит, 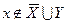 , а это противоречит равенству
, а это противоречит равенству 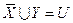 .
.
Отметим, что операция \ выражается через операции  и
и  . По закону де Моргана и закону двойного отрицания справедливо соотношение
. По закону де Моргана и закону двойного отрицания справедливо соотношение  , т. е. операция
, т. е. операция 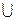 также выражается через операции
также выражается через операции  и
и  . По определению операция
. По определению операция  тоже выражается через
тоже выражается через  и
и  . Таким образом, любая из определенных операций над множествами выражается через операции
. Таким образом, любая из определенных операций над множествами выражается через операции  и
и  .
.
Пересечение и объединение могут быть определены для любого множества множеств  , где индексы
, где индексы  пробегают множество
пробегают множество  . Пересечение
. Пересечение  {
{ 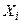 |
|  Î
Î  } и объединение
} и объединение 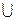 {
{  |
|  Î
Î  } задаются равенствами
} задаются равенствами
 {
{ 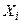 |
| 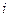 Î
Î  } = {
} = {  |
|  Î
Î 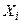 для всех
для всех 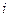 Î
Î  },
},
 {
{ 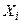 |
| 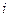 Î
Î  } = {
} = {  |
|  Î
Î  для некоторого
для некоторого 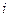 Î
Î  }.
}.
Вместо  {
{ 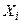 |
| 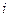 Î
Î  } и
} и 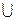 {
{ 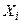 |
| 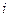 Î
Î  } часто пишут соответственно
} часто пишут соответственно 
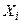 и
и 
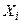 , а иногда просто
, а иногда просто  ,
,  , если из контекста ясно, какое множество I имеется в виду. Если I = {1,2,…, n }, то
, если из контекста ясно, какое множество I имеется в виду. Если I = {1,2,…, n }, то 


 и
и 

 , а также
, а также  и
и 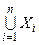 .
.
Совокупность множеств  называется покрытием множества X, если
называется покрытием множества X, если  Если при этом
Если при этом  >0 и
>0 и 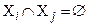 для всех i
для всех i  , то
, то  называется разбиением множества X.
называется разбиением множества X.
Пример. Пусть X ={ a, b, c, d, e, f }. Тогда {{ a, b, d }, { c, f }, { e }} – разбиение множества X, а {{ a, b, d }, { в, c, f }, { в, e }} – покрытие множества X.
Одним из важных понятий теории множеств является понятие декартова произведения множеств. Декартовым (прямым) произведением множеств X и Y называется множество упорядоченных пар вида
 {(x, y)
{(x, y)  x
x 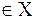 и
и  }.
}.
Пример. Пусть X ={1,2}, Y ={3,4,5}. Тогда  {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5)},
{(1,3), (1,4), (1,5), (2,3), (2,4), (2,5)},  {(3,1), (3,2), (4,1), (4,2), (5,1), (5,2)},
{(3,1), (3,2), (4,1), (4,2), (5,1), (5,2)},  {(1,1), (1,2), (2,1), (2,2)}.
{(1,1), (1,2), (2,1), (2,2)}.
Две пары (x, y) и (u, v) считаются равными тогда и только тогда, когда x = u и y = v
Аналогично можно определить декартово произведение n множеств 

Если  , то n -я степень множества X определяется как
, то n -я степень множества X определяется как 

Пример. Множество  равно множеству равно множеству
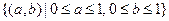 , которому соответствует множество точек на плоско-сти, имеющих неотрицате-льные координаты, не превос-ходящие единицы (рис. 1.6). , которому соответствует множество точек на плоско-сти, имеющих неотрицате-льные координаты, не превос-ходящие единицы (рис. 1.6).
| Рис. 1.6 
|
Мощность множества
1.Пусть заданы два конечных множества X и Y, причем N (X)=  ; N (Y)=
; N (Y)=  , тогда количество элементов в объединении двух множеств X и Y определяется по формуле
, тогда количество элементов в объединении двух множеств X и Y определяется по формуле 

 N(
N( )=N(X)+N(Y)-N(
)=N(X)+N(Y)-N( ).
).
В самом деле, N(X)+N(Y) есть число элементов, которые мы получим, перечисливвсе элементы множества X, а затем – все элементы множества Y. Но в этом случае общие элементы (их число равно 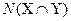 будут перечислены дважды, то есть
будут перечислены дважды, то есть  N(X)+N(Y), откуда и следует приведенная формула.
N(X)+N(Y), откуда и следует приведенная формула.
Справедлива следующая теорема: если  – произвольные множества, то
– произвольные множества, то

(Эта формула доказывается методом математической индукции).
Метод подсчета по данной формуле, состоящий в поочередном сложении и вычитании, называется методом включений и исключений.
2. Для любого разбиения конечного множества


