 |
Геометрический метод минимизации булевой функции
|
|
|
|
Рассмотрим элементарную конъюнкцию ранга r (т.е. содержащую r пропозициональных переменных).
K(X 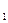 ,...,Xr)=X
,...,Xr)=X 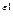 ... Х
... Х 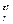 ,
,
где 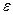 = 0,1; Х
= 0,1; Х 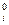 =
= 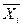 ,
, 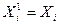 . Очевидно, что множество N
. Очевидно, что множество N  , соответствующее конъюнкции К, есть (3-r)- мерная грань. Число r называется рангом этой грани.
, соответствующее конъюнкции К, есть (3-r)- мерная грань. Число r называется рангом этой грани.
Пример.Конъюнкциям
K 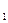 (
(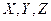 )=
)= 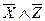
К 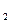 (
(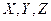 )=
)= 
К 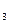 (
(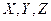 )=
)=  ,
,
соответствуют грани, имеющие ранги 2, 2, и 1. Первые две грани являются одномерной гранью (ребром), а третья - двумерной гранью.
Отметим очевидные свойства введенного соответствия между булевой функцией f и подмножеством 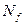 .
.
Если f (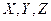 ) = g (
) = g (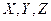 ) Ú h (
) Ú h (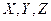 ), то
), то
1)  ,
, 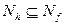 ;
;
2) Nf = Ng 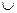 Nh.
Nh.
В частности, если f (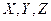 ) обладает ДНФ, т. е.
) обладает ДНФ, т. е.
f (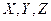 )=
)= 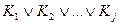 , то
, то 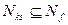 и
и 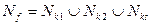 , т.е. ДНФ функции f соответствует покрытие множества N
, т.е. ДНФ функции f соответствует покрытие множества N 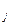 гранями Nk
гранями Nk 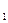 ,., Nks
,., Nks
Пусть r, - ранг грани Nk i (он равен рангу конъюнкции k 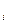 ) Число r, определенное формулой
) Число r, определенное формулой

называется рангом покрытия. Тогда задача о минимизации булевой функции принимает следующую геометрическую постановку: для данного множества 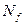 найти такое покрытие гранями, принадлежащими
найти такое покрытие гранями, принадлежащими 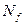 ,
, 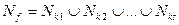 , чтобы его ранг был наименьшим.
, чтобы его ранг был наименьшим.
Приведем также определения сокращенной и тупиковой ДНФ сгеометрической точки зрения.
Грань 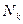 , содержащаяс в
, содержащаяс в 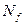 , называется максимальной относительно
, называется максимальной относительно 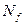 , если не существует грани
, если не существует грани 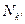 , такой, что
, такой, что
1) 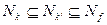 ;
;
2) размерность грани 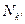 больше размерности грани Nk.
больше размерности грани Nk.
Конъюнкция К, соответствующая максимальной грани 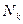 , называется простой импликантой функции f.
, называется простой импликантой функции f.
ДНФ, являющаяся дизъюнкцией всех простых импликант функции f, называется сокращенной ДНФ.
Покрытие множества 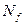 , состоящее из максимальных относительно
, состоящее из максимальных относительно
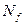 граней, называется неприводимым, если совокупность граней, получающаяся из исходной путем выбрасывания любой грани, не будет покрытием
граней, называется неприводимым, если совокупность граней, получающаяся из исходной путем выбрасывания любой грани, не будет покрытием 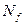 .
.
ДНФ, соответствующая неприводимому покрытию множества 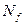 , называется тупиковой в геометрическом смысле.
, называется тупиковой в геометрическом смысле.
|
|
|
Теорема 5.7.1. Понятия тупиковой ДНФ и тупиковой ДНФ в геометрическом смысле эквивалентны.
Алгоритм минимизации функций, зависящих от трех переменных, состоит в следующих четырех шагах:
1. Нанести множество N 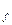 , на трехмерный куб. Использовать или табличное задание функции, отметив вершины, в которых f (
, на трехмерный куб. Использовать или табличное задание функции, отметив вершины, в которых f (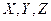 ) = 1, или СДНФ функции и тогда каждому слагаемому СДНФ поставить в соответствие вершину.
) = 1, или СДНФ функции и тогда каждому слагаемому СДНФ поставить в соответствие вершину.
2.Если отмеченными окажутся все вершины куба, то данная функция тождественно истинна.
3. Если отмечены все вершины какой-либо грани, то для построения минимальной формы заменить все четыре вершины одной переменной - названием грани.
4. Если отменены вершины какого-либо ребра то в минимизированной форме им соответствует конъюнкция - название ребра.
Чтобы получить минимизированную форму, надо выбирать ребра, покрывающие вершины так, чтобы меньшим числом ребер покрыть все отмеченные вершины.
5. Если существует вершина, которая не образует ребро ни с какой другой вершиной, то в минимизированной форме ей соответствует конъюнкция - название вершины.
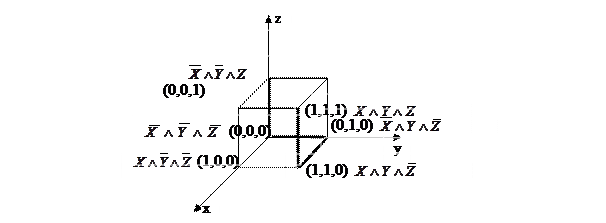
Пример. Минимизировать булеву функцию f (0,1,1)= f (1,0,0)= f (1,0,1)=0 геометрическим методом.
Так как функция задана перечислением наборов, на которых функция принимает значение 0, то на остальных она принимает эначение1, т.е.
f (0,0,0)= f (0,0,1)= f (0,1,0)= f (1,1,0)= f (1,1,1)=1.
На рис. 5.2 изображено геометрическое представление данной булевой функции с указанием наборов и соответствующих им элементарных конъюнкций.

 ;
; 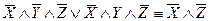 ;
; 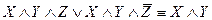 ;
;
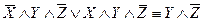 .
.
Из геометрического представления булевой функции следует, что осуществить покрытие вершин можно не единственным образом, поэтому существует для данной булевой функции две различные минимизированные формы 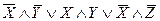 и
и 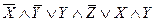 .
.
Замечание. При n= 3 геометрический метод минимизации булевых функций аналогичен минимизации с помощью прямоугольной таблицы, называемой минимизирующей картой (картой Карно) [4].
|
|
|
Задачи и упражнения
1. Упростить следующие ПФ, используя равносильные преобразования:
а) 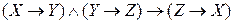 ,
,
б)  ,
,
в) 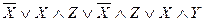 ,
,
г)  ,
,
д) 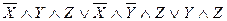 ,
,
е) 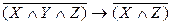 .
.
2. Составить таблицы истинности следующих ПФ и определить их тип:
а)  ,
,
б)  ,
,
в) 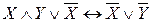 ,
,
г) 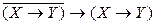 ,
,
д) 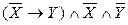 .
.
3. Доказать равносильность
а) 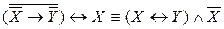 ,
,
б) 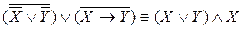 ,
,
в) 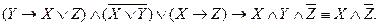
4. Определить конъюнктивное разложение по переменной  следующих ПФ:
следующих ПФ:
а)  ,
,
б) 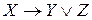 ,
,
в) 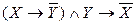 .
.
5. Определить дизъюнктивное разложение по переменной 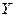 следующих ПФ:
следующих ПФ:
а) 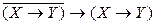 ,
,
б) 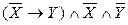 ,
,
в) 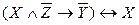 .
.
6. Привести к нормальным и совершенным нормальным формам следующие ПФ:
а)  ,
,
б) 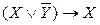 ,
,
в) 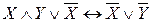 .
.
7. Запишите символически следующие суждения:
а) «вертолет является средством передвижения по воздуху, имеет двигатель, пилотскую кабину, систему управления, несущий винт, помещение для пассажиров или грузов»;
б) «подготовка специалистов высокой квалификации возможна лишь на базе всемерного развития вузовской науки, усиления связи вузовской, академической и отраслевой науки, обеспечения единства научной и учебной работы, широкого привлечения студентов к научным исследованиям»;
в) «если я поеду автобусом и автобус опоздает, то я опоздаю на работу; если я опоздаю на работу и стану огорчаться, то я не попадусь на глаза моему начальнику; если я не сделаю в срок важную работу, то я начну огорчаться и попадусь на глаза моему начальнику. Следовательно, если я поеду автобусом, а автобус опоздает, то я сделаю в срок важную работу».
8. Минимизировать булевы функции методом Квайна и геометрическим методом
а) 
б) 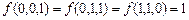
в) 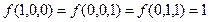 г)
г) 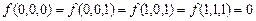
|
|
|


