 |
Основные тождества алгебры множеств
|
|
|
|
Для любых множеств A, B, C справедливы следующие тождества:
1. Коммутативность.
а) A È B = B È A (для объединения);
б) A Ç B = B Ç A (для пересечения).
2. Ассоциативность.
а) A È (B È C) = (A È C) È C (для объединения);
б) A Ç (B Ç C) = (A Ç B) Ç C (для пересечения).
3. Дистрибутивность.
а) A È (B Ç C) = (A È B) Ç (A È C) (для объединения относительно пересечения);
б) A Ç(B È C) = (A Ç B)È(A Ç C) (для пересечения относительно объединения).
4. Закон де Моргана.
а) 
= 
Ç 
(дополнение к объединению есть пересечение дополнений);
б) 
= È (дополнение к пересечению есть объединение дополнений).
5. Идемпотентность.
а) A È A = A (для объединения);
б) A Ç A = A (для пересечения).
6. Поглощение.
а) A È (A Ç B) = A;
б) A Ç (A È B) = A.
7. Расщепление (склеивание).
а) (A È B) Ç (A È ) = A;
б) (A Ç B) È (A Ç ) = A.
8. Двойное дополнение.
= A.
9. Закон исключенного третьего. 
A È = U.
10. Операции с пустым и универсальным множествами.
а) A È U = U;
б) A È Æ = A;
в) A Ç U = A;
г) A Ç Æ = Æ;
д) 
= U;
е) 
= Æ.
11. А \ В = A Ç .
Чтобы доказать некоторое тождество A = B, нужно доказать, что, во-первых, если x Î А, то x Î В и, во-вторых, если x Î В, то x Î А. Докажем таким образом, например, свойство дистрибутивности для объединения (тождество 3а)):
A È (B Ç C) = (A È B) Ç (A È C).
1. Сначала предположим, что некоторый элемент x принадлежит левой части тождества, т.е. x Î A È (B Ç C), и докажем, что x принадлежит правой части, т.е. x Î(A È B) Ç (A È C).
Действительно, пусть x Î A È (B Ç C). Тогда либо x Î A, либо x Î B Ç C. Рассмотрим каждую из этих возможностей.
Пусть x Î A. Тогда x Î A È B и x Î A È C (это верно для любых множеств B и C). Следовательно, x Î(A È B) Ç (A È C).
|
|
|
2. Предположим, что некоторый элемент x принадлежит правой части тождества, т.е. x Î (A È B) Ç (A È C), и докажем, что x принадлежит левой части, т.е. x Î A È (B Ç C).
Действительно, пусть x Î (A È B) Ç (A È C). Тогда x Î A È B, и одновременно x Î A È C. Если x Î A È B, то либо x Î A, либо x Î B, если. x Î A È C, то либо x Î A, либо x Î C. Пусть x Î A, Тогда x Î A È (B Ç C) и утверждение доказано. Если x Ï A, то одновременно должны выполняться условия x Î B и x Î C, т.е. x Î B Ç C. Но тогда x Î B Ç C и x Î A È (B Ç C), что также доказывает наше утверждение.
Доказательство тождеств можно проиллюстрировать с помощью диаграмм Венна.
Основные тождества алгебры множеств можно использовать для доказательства других тождеств.
Пример 1.14.
Доказать тождество (A È B) \ В = A Ç .
Преобразуем левую часть тождества, используя тождество 11:
(A È B) \ В = (A È B) Ç .
Затем используем закон дистрибутивности (тождество 3б):
(A È B) Ç = A Ç È B Ç .
Используем закон исключенного третьего (тождество 9):
B Ç = Æ.
Получим
A Ç È B Ç = A Ç È Æ.
Используем свойство пустого множества (тождество 10б):
A Ç È Æ = A Ç .
Тождество доказано.
Пример 1.15.
Доказать тождество:
A \ (В \ C) = (A \ В)È (A Ç C).
Множества, стоящие в левой и правой частях тождества, изобразим с помощью диаграмм Эйлера – Венна (рис. 1.2).
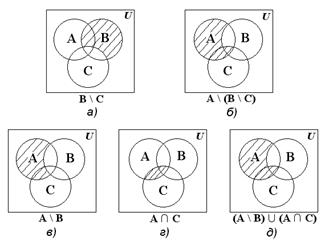
Рис. 1.2
Рис. 1.2 б) и рис. 1.2 д) иллюстрируют равенство множеств A \ (В \ C) и (A \ В)È (A Ç C).
Докажем тождество из нашего примера, воспользовавшись тождествами:
А \ В = A Ç , = È , 
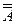= A, A Ç(B È C) = (A Ç B)È(A Ç C).
Получим:
A \ (В \ C) = A Ç 
= A Ç 
= A Ç (
È 
) = A Ç ( È C) = (A Ç ) È (A Ç C) = (A \ В)È (A Ç C).
Основные тождества алгебры множеств можно также использовать для упрощения формул алгебры логики.
|
|
|
Пример 1.16.
Упростить выражение:
(A È B) Ç ( È B) Ç (A È ).
Используя закон коммутативности (тождество 1б), поменяем местами вторую и третью скобки:
(A È B) Ç ( È B) Ç (A È ) = (A È B) Ç (A È ) Ç ( È B).
Применим закон расщепления (тождество 7а) для первой и второй скобок:
(A È B) Ç (A È ) Ç ( È B) = A Ç ( È B).
Воспользуемся законом дистрибутивности (тождество 3б):
A Ç ( È B) = A Ç È A Ç B.
Используем закон исключенного третьего (тождество 9):
A Ç = Æ.
Получим
A Ç È A Ç B = Æ È A Ç B.
Используем свойство пустого множества (тождество 10б):
Æ È A Ç B = A Ç B.
Итак,
(A È B) Ç ( È B) Ç (A È ) = A Ç B.
Эквивалентность множеств
Определение 1.2. Если каждому элементу множества A сопоставлен единственный элемент множества B и при этом всякий элемент множества B оказывается сопоставленным одному и только одному элементу множества A, то говорят, что между множествами A и B существует взаимно однозначное соответствие. Множества A и B в этом случае называют эквивалентными или равномощными.
Эквивалентность множеств обозначается следующим образом: A ~ B.
Эквивалентность множеств обладает следующим свойством транзитивности.
Если A ~ B и B ~ C, то A ~ C.
Докажем это свойство. Так как A ~ B, то для всякого элемента a Î А существует единственный элемент b Î B. Но так как B ~ C, то для всякого элемента b Î B существует единственный элемент c Î C. Сопоставим этот элемент элементу a Î А. Значит, для всякого элемента a Î А существует единственный элемент c Î C и для всякого элемента c Î C существует единственный элемент a Î А. Следовательно, A ~ C.
Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда количество элементов в них одинаково. Например, множества А = {4, 5, 6} и В = { x, y, z } эквивалентны, A ~ B. Взаимно однозначное соответствие может быть установлено между элементами 4 и x, 5 и y, 6 и z.
Мощностью конечного множества А (обозначается ç А ç) называется число элементов этого множества. Например, мощность множества А = {1, 2} равна ç А ç= 2.
Пример 1.17.
Ранее (разд. 1.1) мы рассматривали множество всех подмножеств данного множества А, которое называется множеством-степенью и обозначается P (A). Множество P (A) состоит из 2 n элементов. Таким образом, ç P (A) ç = 2 n.
|
|
|
Рассмотрим задачу определения мощности объединения n конечных множеств.
Пусть n = 2 и A и B – два пересекающихся множества. Докажем с помощью диаграммы Эйлера – Венна следующее соотношение:
ç А È B ç= ç А ç+ ç B ç– ç А Ç B ç. (1.1)
Из рис. 1.3 видим, что
ç А È B ç= n 1+ n 2+ n 3;
ç А ç= n 1+ n 2;
ç B ç= n 2+ n 3;
ç А Ç B ç= n 2.
Рис. 1.3
Очевидно, что n 1+ n 2+ n 3 = (n 1+ n 2) +(n 2+ n 3) – n 2, что и доказывает формулу ().
Формула (1.1) справедлива и для случая, если множества A и B не пересекаются. В этом случае
ç А È B ç= ç А ç+ ç B ç.
Пусть n = 3 и A, B и С – три пересекающихся множества. В этом случае справедливо следующее соотношение:
ç А È B È С ç= ç А ç+ ç B ç+ ç C ç– ç А Ç B ç– ç А Ç C ç– ç B Ç C ç+ ç А Ç B Ç C ç. (1.2)
Из рис. 1.4 видим, что
ç А È B È С ç= n 1+ n 2+ n 3+ n 4+ n 5+ n 6+ n 7;
ç А ç= n 1+ n 2+ n 4+ n 5;
ç B ç= n 2+ n 3+ n 5+ n 6;
ç С ç= n 4+ n 5+ n 6+ n 7;
ç А Ç B ç= n 2+ n 5;
ç А Ç C ç= n 4+ n 5;
ç B Ç C ç= n 5+ n 6;
ç А Ç B Ç C ç= n 5.
Рис. 1.4
Очевидно, что
n 1+ n 2+ n 3+ n 4+ n 5+ n 6+ n 7 =(n 1+ n 2+ n 4+ n 5) + (n 2+ n 3+ n 5+ n 6) +(n 4+ n 5+ n 6+ n 7) – (n 2+ n 5) – (n 4+ n 5) – (n 5+ n 6) + n 5,
что и доказывает формулу (1.2).
Формула (1.2) справедлива и для случая, если множества A, B и С попарно не пересекаются. В этом случае
ç А È B È С ç= ç А ç+ ç B ç+ ç C ç.
В общем случае мощность объединения n множеств определяется по формуле:
ç А 1È А 2 È…È Аn ç= ç А 1ç+ç А 2ç+…+ ç Аn ç– (ç А 1Ç А 2ç+ ç А 1Ç А 3ç+ … +ç Аn –1Ç Аn ç)+ ç А Ç B Ç C ç+ (ç А 1Ç А 2 Ç А 3ç + … +ç Аn –2Ç Аn –1Ç Аn ç) – … + (–1) n – 1 ç А 1Ç А 2 …Ç Аn ç. (1.3)
Эта формула выводится индукцией по n, [3].
Если множества Аi попарно не пересекаются, т.е. Аi Ç Аj = Æ, i ¹ j,то получим частный случай формулы (1.3):
|
|
|
ç А 1È А 2 È…È Аn ç= ç А 1ç+ç А 2ç+…+ ç Аn ç.
В общем случае справедливо неравенство
ç А 1È А 2 È…È Аn ç£ ç А 1ç+ç А 2ç+…+ ç Аn ç.
Понятие эквивалентности годится и для бесконечных множеств. Пусть, например, A = {1, 2, 3, …, n,…}, B = {– 1, –2, …, – n, …}. Тогда A ~ B. Взаимно однозначное соответствие устанавливается по правилу: элементу n Î A соответствует элемент – n Î B, т.е. n «– n.
Пример 1.18.
A = {1, 2, 3, …, n,…}, B = {2, 4 …, 2 n, …}. Тогда A ~ B. Взаимно однозначное соответствие устанавливается по правилу: n «2 n.
Пример 1.19.
A = {1, 2, 3, …, n,…} – множество натуральных чисел, B = {…, – n, …– 2, –1, 0, 1, 2, …, n, …} – множество всех целых чисел.
Перепишем множество B следующим образом:
B = {0, –1, 1, – 2, 2, …, – n, n, …}, так, что 0 будет на первом месте, –1 на втором, 1 на третьем, –2 на четвертом и т.д. Нетрудно заметить, что отрицательные числа будут стоять на местах с четными номерами, а 0 и положительные числа – на местах с нечетными номерами. Поэтому взаимно однозначное соответствие между множествами A и B устанавливается по правилу: для всякого n ³ 0 элементу a = 2 n +1 из множества A (т.е. нечетному элементу) соответствует элемент b = n из множества B; элементу a = 2 n из множества A (т.е. четному элементу) соответствует элемент b = – n из множества B. Таким образом, реализуется взаимно однозначное соответствие между множествами A и B: 1 «0, 2 «–1, 3 «1, 4 «–2 и т.д.
Примеры 1.18 и 1.19 показывают, что множество может быть эквивалентно своему подмножеству. Так, в примере 1.18 B Ì A, а в примере 1.19 A Ì B. И в том, и в другом случае A ~ B.
Установить эквивалентность множеств, т.е. установить взаимно однозначное соответствие между их элементами можно различными путями. На рис. 1.5 показано, что множества точек двух отрезков [ a, b ] и [ c, d ] эквивалентны.
Рис.1.5
Таким же образом можно установить эквивалентность множеств точек двух интервалов. На рис.1.6 показано, что множества точек любого интервала (a, b) эквивалентно множеству точек всей прямой.
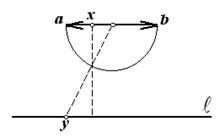
Рис. 1.6
Для установления эквивалентности двух множеств можно применять следующую теорему.
Теорема Бернштейна. Если множество A эквивалентно части множества B, а множество B эквивалентно части множества A, то множества A и B эквивалентны.
Применим теорему Бернштейна для доказательства того, что множество точек любого отрезка эквивалентно множеству точек любого интервала.
Пусть A = [ a, b ] – произвольный отрезок, а B = (c, d) – произвольный интервал.
Пусть A 1 = [ a 1, b 1] – любой внутренний интервал отрезка [ a, b ], A 1Ì A. Тогда A 1 ~ B.
Пусть B 1 = (c 1, d 1) – любой внутренний отрезок интервала (c, d), B 1Ì B. Тогда B 1 ~ A.
|
|
|
Таким образом, выполняются условия теоремы Бернштейна. Поэтому A ~ B.
Итак, все интервалы, отрезки и вся прямая эквивалентны между собой.
Счетные множества
Определение 1.3. Множество, эквивалентное множеству натуральных чисел N = {1, 2, 3, …, n,…}, называется счетным.
Можно сказать также, что множество счетно, если его элементы можно перенумеровать.
Пример 1.20.
Следующие множества являются счетными.:
1. A 1 = {–1, –2, …, – n, …};
2. A 2 = {2, 22, …, 2 n,…};
3. A 3 = {2, 4, …, 2 n,…};
4. A 4 = {…, – n, …, – 1, 0, 1, …, n,…};
Чтобы установить счетность некоторого множества, достаточно указать взаимно однозначное соответствие между элементами данного множества и множества натуральных чисел. Для примера 1.19 взаимно однозначное соответствие устанавливается по следующим правилам: для множества A 1: – n «n; для множества A 2: 2 n «n; для множества A 3: 2 n «n; счетность множества A 4 установлена в примере 1.19;
Установить счетность множеств можно также, используя следующие теоремы о счетных множествах (приводятся без доказательств).
Теорема 1. Всякое бесконечное подмножество счетного множества счетно.
Пример 1.21.
Множество A = {3, 6, …, 3 n,…} счетно, т.к. A – бесконечное подмножество множества натуральных чисел, A Ì N.
Теорема 2. Объединение конечной или счетной совокупности счетных множеств счетно.
Пример 1.22.
Множество A = {0, 1, …, n,…} неотрицательных целых чисел счетно, множество B = {0, –1, …, – n,…} неположительных целых чисел тоже счетно, поэтому множество всех целых чисел С = А È B = {…, – n, …– 2, –1, 0, 1, 2, …, n, …} тоже счетно.
Теорема 3. Множество всех рациональных чисел, т.е. чисел вида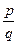 
, где p и q целые числа, счетно.
Теорема 4. Если А = { a 1, a 2, …} и B = { b 1, b 2, …} – счетные множества, то множество всех пар С = {(ak, bn), k = 1, 2,…; n = 1, 2, …} счетно.
Пример 1.23.
Геометрический смысл пары (ak, bn) – точка на плоскости с рациональными координатами (ak, bn). Поэтому можно утверждать, что множество всех точек плоскости с рациональными координатами счетно.
Теорема 5. Множество всех многочленов P (x) = a 0 + a 1 x + a 2 x2 + … + anxn любых степеней с рациональными коэффициентами a 0, a 1, a 2, … an счетно.
Теорема 6. Множество всех корней многочленов любых степеней с рациональными коэффициентами счетно.
|
|
|
