 |
Особенности цифрового управления
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ»
Теория автоматического управления
Методические указания
Для курсового и дипломного проектирования
Для студентов специальности 1-53 01 01-05 Автоматизация технологических процессов и производств (легкая промышленность),
Раздел: Проектирование дискретных систем автоматического управления
Витебск
УДК 681. 5
Теория автоматического управления методические указания для курсового и дипломного проектирования для студентов специальности 1-53 01 01-05 «Автоматизация технологических процессов и производств (легкая промышленность)», раздел: «Проектирование дискретных систем автоматического управления»
Витебск: Министерство образования РБ, УО «ВГТУ», 2008.
Составители: доцент, к.т.н. Иванова Л.В.
ассистент Леонов В.В.
ст. преподаватель Ринейский К.Н.
Методические указания содержат элементы теории дискретных САУ, особенности построения псевдочастотных логарифмических характеристик (ПЛАЧХ) цифровых систем и их использование для выбора структуры параметров КУ непрерывного и дискретного типа, выбора оптимального алгоритма цифрового управляющего устройства. Рассмотрен пример проектирования дискретной САУ с заданными свойствами, определения периода дискретности и выбора дискретного КУ. Приведены алгоритмы цифровых регуляторов и их настройки.
Методические указания составлены в соответствии с программой курса ТАУ, раздел: «Проектирование дискретных систем автоматического управления», изучаемого студентами специальности 1-53 01 01-05 для выполнения курсовых и дипломных проектов, а также могут использоваться для подготовки к госэкзаменам, к курсовым проектам по курсам АЭПО и АТПП и др.
|
|
|
Одобрено кафедрой АТПП УО «ВГТУ» «07» февраля 2008 г., протокол № 7.
Рецензент: ст. преподаватель Давыдько А.П.
Редактор: доцент, к.т.н. Смелков Д.В.
Рекомендовано к опубликованию редакционно-издательским советом УО «ВГТУ» «___»__________2008 г., протокол № ___
Ответственный за выпуск Букин Ю.А.
Учреждение образования «Витебский государственный технологический университет»
________________________________________________________________
Подписано к печати__________ Формат___________. Уч.-изд.л.__________
Печать ризографическая. Тираж _____ экз. Заказ № _____. Цена _______р.
Отпечатано на ризографе Учреждения образования «Витебский государственный технологический университет».
Лицензия № 02330/0133005 от 1 апреля 2004 г.
210035, Витебск, Московский проспект, 72.
СОДЕРЖАНИЕ
| 1 Дискретные САУ………………………………………….. | ||
| 1.1 Импульсные и цифровые САУ | ||
| 1.2 Особенности цифрового управления…………………… | ||
| 1.3 Проектирование дискретных систем с заданными свойствами (расчет периода дискретности, коэффициента усиления, построение ЛАЧХ)………………………………… | ||
| 1.4 Определение структуры и параметров корректирующего устройства (непрерывного и дискретного) и реализация дискретного устройства……………………………………………………… | ||
| Выводы………………………………………………………… | ||
| Список использованной литературы………………………… |
Дискретные САУ
Импульсные и цифровые САУ
Импульсные системы – это системы, в которых действуют сигналы квантованные по времени. Импульсный элемент осуществляет квантование непрерывного сигнала x(t) по времени, преобразуя его в дискретный сигнал x*(t). Квантование называют импульсной модуляцией, которая заключается в изменении одного из параметров выходных импульсов (модулируемого параметра) в функции величины входного (модулирующего) сигнала. Модулируемым параметром для последовательности импульсов на выходе импульсного элемента (ИЭ) может быть высота (амплитуда) импульса, его ширина или пауза между импульсами. Соответственно существуют три вида импульсной модуляции: амплитудно-импульсная модуляция (АИМ), широтно-импульсная модуляция (ШИМ) и время-импульсная модуляция (ВИМ). Последняя подразделяется на фазо-импульсную модуляцию (ФИМ) и частотно-импульсную модуляцию (ЧИМ). Во всех случаях форма импульсов принимается неизменной.
|
|
|
При АИМ модулируемым параметром, зависящим от значения входного сигнала ИЭ x(t) в начале очередного периода Т0 повторения импульсов, является высота (амплитуда) импульсов А.
При ШИМ модулируемым параметром является ширина импульса Тn при постоянном периоде Т0 повторения импульсов.
При ФИМ модулируемым параметром является запаздывание tзап относительно начала периодов при постоянном Т0.
При ЧИМ – модулируемым параметром является частота ln 
 следования импульсов, изменяющаяся в зависимости от x(t).
следования импульсов, изменяющаяся в зависимости от x(t).
Соответственно по виду модуляции системы с АИМ относят к классу линейных дискретных систем и с ШИМ, если пренебречь эффектом квантования по уровню. Эти системы получили наибольшее распространение.
Основное достоинство дискретных систем:
а) возможность многоточечного (многоканального) управления;
б) многократное использование линий связи;
в) повышенная помехозащищенность.
Первое достоинство заключается в том, что с помощью одного управляющего устройства (УУ) можно управлять несколькими объектами путем циклического подключения УУ последовательно к каждому УО. Система управления существенно упрощается по сравнению со случаем применения УУ для каждого объекта.
Возможность многократного использования одного канала связи для управления несколькими объектами, удаленными от места расположения УУ основана на том же принципе последовательного подключения объектов и соответствующих УУ линий связи с помощью синхронно действующих на обоих концах линий связи (шаговых) распределителей. Это временное разделение каналов.
|
|
|
Повышенная помехозащищенность обусловлена возможностью передавать информацию в виде очень коротких импульсов, в промежутке между которыми система оказывается разомкнутой и не реагирует на внешние возмущения.
Линейная система импульсного регулирования
Линейной системой импульсного регулирования называется такая система автоматического регулирования (САР), которая кроме звеньев непрерывного действия содержит импульсное звено, преобразующее непрерывный сигнал в равноотстоящие друг от друга импульсы.
Варианты выходных последовательностей импульсных звеньев (рис. 1).

Рисунок 1 – Выход импульсного звена

Рисунок 2 – Пример импульсной системы
1 – импульсное звено – ключ с ШИМ; 2 – непрерывное звено – фильтр с нагрузкой; изменение  можно рассматривать как возмущение
можно рассматривать как возмущение  .
.
Система линейна, если линеен ШИ-модулятор. Если  меняется, то система дополнительно будет параметрической.
меняется, то система дополнительно будет параметрической.
Математический аппарат описания импульсных систем
Непрерывная функция  может быть представлена решетчатой функцией
может быть представлена решетчатой функцией  .
.

Рисунок 3 – Решетчатые функции
Решетчатые функции 2 определены только в дискретные моменты времени [ nT ] (сокращенно [ n ]) и формируются из непрерывных функций 1: f [ nT ] = f (t) при t = nT. Рассматривают также смещенные решетчатые функции (последовательность 3): f [ n,ε] = f (t) при t =(n +ε) T, где ε-относительное смещение,  .
.
 - безразмерное время;
- безразмерное время;  .
.
Непрерывные функции, проходящие через дискреты заданной решетчатой функции, называют огибающими. Их бесконечно много.
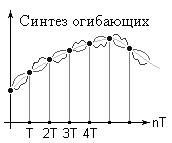
Рисунок 4 – Синтез огибающих
Основная огибающая может быть получена, как результат решения ДУ наименьшего порядка и должна содержать гармоники наименьшей частоты.
Для решетчатых функций времени вводится понятие дискретного преобразования Лапласа.
 , (1)
, (1)
где 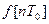 - решетчатая функция (n=1,2,3…);
- решетчатая функция (n=1,2,3…);
 - период повторения дискретных значений решетчатой функции;
- период повторения дискретных значений решетчатой функции;
 - дискретное изображение функции
- дискретное изображение функции 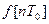 ;
;
 - символ дискретного преобразования.
- символ дискретного преобразования.
|
|
|
Для решетчатой функции в относительном времени  , формула дискретного преобразования принимает вид:
, формула дискретного преобразования принимает вид:
 , (2)
, (2)
где  - новая безразмерная комплексная переменная,
- новая безразмерная комплексная переменная,  ;
;  - относительная частота
- относительная частота 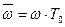 ;
;  - абсцисса сходимости ряда.
- абсцисса сходимости ряда.
Введем обозначение 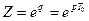 , и тогда выражение (1) примет вид:
, и тогда выражение (1) примет вид:
 (3)
(3)
и соответствует 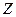 -преобразованию дискретного сигнала,
-преобразованию дискретного сигнала, 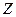 - символ этого преобразования.
- символ этого преобразования.
Дискретное преобразование Лапласа аналогично обычному непрерывному преобразованию Лапласа для непрерывных функций:
 (4)
(4)
с переходом от интеграла к сумме в соответствии с дискретным характером оригинала.
Найдем изображение Лапласа идеальной импульсной функции, которую можно представить в виде
 ,
,
где  - модулирующая функция.
- модулирующая функция.
Эта функция представляет собой последовательность δ-импульсов, существующих в моменты  , где n=1,2…, и имеющих площадь, равную значению непрерывной функции
, где n=1,2…, и имеющих площадь, равную значению непрерывной функции  в эти дискретные моменты.
в эти дискретные моменты.
Изображение Лапласа этой функции в соответствии с формулой (4):
 .
.
Это выражение совпадает с формулой (1), т.е. дискретное преобразование Лапласа совпадает с обычным преобразованием Лапласа идеальной импульсной функции. Поэтому в импульсных системах дискретные сигналы можно трактовать как решетчатые функции и как идеальные импульсные функции.
Основные свойства дискретного преобразования Лапласа
1. Изображение дискретного сигнала периодично вдоль мнимой оси и полностью определено в полосе соответствующей изменению относительной частоты в диапазоне ±π, т.е. -p<v<p
 , где k = 0,1,2,3…
, где k = 0,1,2,3…
2. Суммирование в области оригиналов соответствует делению изображения на 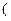
 ) (аналог операции интегрирования непрерывных сигналов).
) (аналог операции интегрирования непрерывных сигналов).
 .
.
3. Формулы для предельных значений решетчатой функции, выраженные через дискретные изображения:
 начальное значение
начальное значение
 конечное значение
конечное значение
4. Изображение решетчатой функции, смещенной в сторону запаздывания на m периодов:

5. Оригинал функции в дискретные моменты времени можно определить по формуле обратного Z-преобразования:
 , интегрирование ведется вдоль единичной окружности Г, а также по сумме вычетов по всем корням Z – характеристического уравнения
, интегрирование ведется вдоль единичной окружности Г, а также по сумме вычетов по всем корням Z – характеристического уравнения  .
.
Спектры дискретных сигналов
Дискретный сигнал можно записать в нескольких формах:

где  - импульс, сдвигаемый во времени, является периодической функцией, которая может быть представлена рядом Фурье в комплексной форме:
- импульс, сдвигаемый во времени, является периодической функцией, которая может быть представлена рядом Фурье в комплексной форме:
 ,
,
где  , а
, а  .
.
Поэтому  , а дискретный сигнал можно записать в форме
, а дискретный сигнал можно записать в форме 
Спектр дискретного сигнала  получим, взяв преобразование Фурье:
получим, взяв преобразование Фурье:

Интеграл, стоящий под знаком суммы,
|
|
|

 .
.
Составляющие ряда при  называются транспонированными составляющими.
называются транспонированными составляющими.
Частотные характеристики дискретного сигнала в соответствии с последней формулой можно получить через частотные характеристики непрерывного сигнала, смещая их на 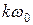 и суммируя ординаты с последующим доумножением на
и суммируя ординаты с последующим доумножением на  . Особенностью спектра дискретного сигнала является его периодичность по оси частот с периодом
. Особенностью спектра дискретного сигнала является его периодичность по оси частот с периодом  , поэтому их рассматривают в полосе частот
, поэтому их рассматривают в полосе частот  или
или  , для других частот картина повторяется.
, для других частот картина повторяется.
Если транспонированные составляющие спектра дискретного сигнала не перекрываются (не накладываются), то по дискретным значениям без потери информации можно восстановить непрерывный сигнал. Это возможно, если спектр непрерывной функции  ограничен частотой
ограничен частотой  , а частота импульсного элемента
, а частота импульсного элемента  выбирается так, чтобы
выбирается так, чтобы  или
или  .
.
Разностные уравнения
Системы, в которых действуют сигналы в виде решетчатых функций, могут быть описаны с помощью разностных уравнений. Для решения таких уравнений можно воспользоваться методами классической теории разностных уравнений, которые аналогичны методам теории дифференциальных уравнений. Однако значительно проще использовать преобразование Лапласа в дискретной форме.
Рассмотрим порядок решения разностных уравнений с помощью дискретного преобразования Лапласа. Разностное уравнение имеет вид:

Это линейное неоднородное уравнение m-го порядка.
 - первая разность (разность первого порядка), она характеризует скорость изменения решетчатой функции и является аналогом первой производной непрерывной функции.
- первая разность (разность первого порядка), она характеризует скорость изменения решетчатой функции и является аналогом первой производной непрерывной функции.
 - вторая разность (аналог второй производной)
- вторая разность (аналог второй производной)

В общем виде m -я разность
 ,
,
где  - коэффициенты бинома Ньютона.
- коэффициенты бинома Ньютона.
Аналогично  - l -ая разность функции
- l -ая разность функции 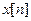 .
.
Разностное уравнение можно записать в виде рекуррентного уравнения через полные значения решетчатых функций; используя выражение для m -ой разности.
 . (5)
. (5)
Введем оператор, связывающий последующее значение решетчатой функции с предыдущим, т.е.  с
с  . Обозначив его
. Обозначив его  , можно записать:
, можно записать:
 ,
,

 ,
, 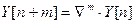 .
.
Оператор  – называют обратной разностью или оператором сдвига. С его помощью уравнение (69) можно представить в виде:
– называют обратной разностью или оператором сдвига. С его помощью уравнение (69) можно представить в виде:
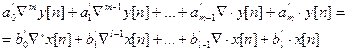 (6)
(6)
или в виде
 ,
,
где

и ввести передаточную функцию
 .
.
Решение разностных уравнений с помощью дискретного преобразования Лапласа аналогично решению дифференциального уравнения с помощью обычного преобразования Лапласа.
Вначале над обеими частями уравнения совершают прямое преобразование Лапласа и находят выражение для дискретного изображения искомой функции. Затем по нему находят оригинал (функцию времени), пользуясь таблицами и разлагая предварительно полученное выражение для изображений на простые слагаемые (дроби).
Выражение для дискретного изображения Y(z) получается из уравнения, использующего оператор сдвига  , точно так же, как выражение для изображения непрерывной функции получается из дифференциального уравнения с оператором дифференцирования p. Оператор
, точно так же, как выражение для изображения непрерывной функции получается из дифференциального уравнения с оператором дифференцирования p. Оператор  играет роль подобную оператору p.
играет роль подобную оператору p.
Если совершить над разностным уравнением (70) дискретное преобразование Лапласа при нулевых начальных условиях, получим выражение для дискретного изображения искомой функции (в Z -форме):
 ,
,
где  - дискретная передаточная функция, которая получается простой заменой
- дискретная передаточная функция, которая получается простой заменой  и
и  .
.
Z -преобразование (Z -изображение) типовых решетчатых функций и типовых непрерывных передаточных функций W(p) сведены в таблицы. Определены правила и теоремы для математических манипуляций с ними. [2, 6].
Разностные уравнения легко машинизируются и для их расчета можно составлять рекуррентный алгоритм.
Типовая структура импульсной системы с АИМ. Понятие об импульсном фильтре

Рисунок 5 – Структура импульсной системы
Если время замкнутого состояния ключа мало, то сигнал на его выходе можно заменить последовательностью дельта-функций с площадью  , т.е:
, т.е:  .
.
В таком случае реакция непрерывной части 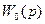 - это суперпозиция весовых функций
- это суперпозиция весовых функций 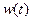 , которую можно рассматривать и как непрерывный сигнал
, которую можно рассматривать и как непрерывный сигнал  , и как дискретную последовательность
, и как дискретную последовательность  .
.
Импульсным фильтром считают импульсный элемент (ключ) с непрерывной частью 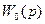 на выходе. За истинный сигнал фильтра принимают выходную последовательность только в дискретные моменты времени
на выходе. За истинный сигнал фильтра принимают выходную последовательность только в дискретные моменты времени  , где n = 1, 2, 3...
, где n = 1, 2, 3...

Рисунок 6 – Идеальный импульсный элемент с АИМ
Задача идеального импульсного элемента (ИИЭ) в модели - сформировать для дальнейшего математического описания системы либо последовательность импульсов типа δ-функций с площадью ~ x (t), либо решетчатую функцию, в основе которой единичная импульсная функция  с амплитудой ~ x (t).
с амплитудой ~ x (t).
Задача экстраполятора - математически описать выходную последовательность реального импульсного звена между значениями решетчатой функции (экстраполяция - это прогнозирование (синтез) сигнала по истории выборок вплоть до следующего достоверного значения, которое в текущий момент не известно, и, получив которое, можно провести историческую коррекцию прогноза - интерполяцию).
Коэффициент передачи квантователя (ИИЭ) обратно пропорционален периоду квантования, а коэффициент передачи экстраполятора нулевого порядка равен периоду. Таким образом общий коэффициент передачи квантующей и восстанавливающей цепи, т.е. ИЭ обычно равен единице.
Приведенные весовая и передаточная функции разомкнутой импульсной системы
Если ИИЭ выдает решетчатую функцию, то можно ввести понятие «приведенной весовой функции» -  . Это отношение выходного сигнала y (t) к значению единственной дискреты
. Это отношение выходного сигнала y (t) к значению единственной дискреты  , поданной на вход экстраполятора.
, поданной на вход экстраполятора.
Если ИИЭ выдает последовательность типа δ -функций, то для непрерывной части совместно с экстраполятором можно вывести понятие приведенной непрерывной передаточной функции:
 ,
,
при этом
 .
.
Знание приведенной решетчатой весовой функции  позволяет найти реакцию импульсного фильтра на входную величину произвольного вида - x (t). Рассмотрим реакции на отдельные значения входной величины в дискретные моменты времени:
позволяет найти реакцию импульсного фильтра на входную величину произвольного вида - x (t). Рассмотрим реакции на отдельные значения входной величины в дискретные моменты времени:
на  ,
,
на  ,
,
на  .
.
Следовательно, реакция на всю входную последовательность будет равна

Здесь первоначально изменен порядок суммирования (свертка), а затем учтено запаздывание оператором запаздывания  . Если устремить n к бесконечности, то, очевидно, что сомножитель для x [ n ] есть дискретная ПФ:
. Если устремить n к бесконечности, то, очевидно, что сомножитель для x [ n ] есть дискретная ПФ:
 .
.
И поскольку она является Z -преобразованием приведенной решетчатой весовой функции, то ее можно представить как Z -преобразование от обратного преобразования Лапласа приведенной ПФ экстраполятора и непрерывной части:
 .
.
Часто для краткости записи знак операции 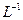 опускают записывая
опускают записывая  .
.
Правила преобразования структурных схем дискретных систем

Рисунок 7 – Соединение звеньев
1. 
 .
.
2. 
 , т.е.
, т.е.  .
.
3.  .
.
4.  ,
,
где  - относительное смещение, которое отсчитывается от начала предыдущего такта
- относительное смещение, которое отсчитывается от начала предыдущего такта  .
.
ПФ системы с экстраполятором нулевого порядка и звеном запаздывания

а) б)
Рисунок 8 – Структура с экстрополятором
Экстраполятором нулевого порядка являются: 1) УВХ и 2) ЦАП. На выходе его ступенчатый сигнал (рис. 8 а). Найдем изображение Лапласа для единичного импульса, рассматривая его как разнополярные скачкообразные воздействия со сдвигом.

Рисунок 9 – Единичный импульс
 ,
,  .
.
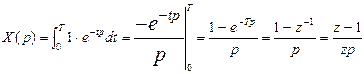 .
.
Тогда z – изображение экстраполятора и непрерывной части со звеном запаздывания (приведенная передаточная функция):
 .
.
 не учитывает коэффициент передачи ИИЭ равный
не учитывает коэффициент передачи ИИЭ равный  ;
; 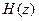 - изображение переходной функции.
- изображение переходной функции.
ПФ системы с экстраполятором, осуществляющим АМ первого или второго рода

Рисунок 10 – Выход модулятора и структура системы
Найдем изображение Лапласа для частично заполненного импульса.
 - скважность (площадь импульса к произведению
- скважность (площадь импульса к произведению 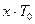 ,
,  .
.
 .
.
Если  , то
, то  , тогда
, тогда
 - приведенная передаточная функция. К этой формуле в первом приближении сводится АМ второго рода. Таким образом, передаточная функция непрерывной части зависит от формы сигнала на выходе ФИ или экстраполятора:
- приведенная передаточная функция. К этой формуле в первом приближении сводится АМ второго рода. Таким образом, передаточная функция непрерывной части зависит от формы сигнала на выходе ФИ или экстраполятора:
 - при формировании импульсов и
- при формировании импульсов и  - при ступенчатом сигнале.
- при ступенчатом сигнале.
ПФ замкнутой импульсной системы

Рисунок 11 – Структура импульсной системы с запаздыванием
Опишем систему в изображениях Лапласа:

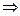
 ;
;
 или
или  ,
,
т.е. ПФ замкнутой импульсной системы

ПФ по ошибке  может быть получена решением системы относительно ошибки x.
может быть получена решением системы относительно ошибки x.
Поскольку запаздывание не определяет свойства системы в области низких частот, практически всегда для оценки качества могут быть использованы формулы
 - передаточная функция;
- передаточная функция;
 - передаточная функция ошибки относительно задающего воздействия (осталась особенность
- передаточная функция ошибки относительно задающего воздействия (осталась особенность  , см. правила преобразования структурных схем).
, см. правила преобразования структурных схем).
ПФ для возмущений

Рисунок 12 – Структура при наличии возмущений
Поскольку для произведения двух операторных многочленов  (изображение возмущения) и
(изображение возмущения) и  нельзя найти z-преобразование раздельно, то ПФ по возмущению удобно определять для эквивалентных возмущений
нельзя найти z-преобразование раздельно, то ПФ по возмущению удобно определять для эквивалентных возмущений  , приведенных к входу ИЭ:
, приведенных к входу ИЭ:
 .
.
Частотные ПФ импульсных систем
ПФ W (z) при подстановке  - есть частотная ПФ. Все остается в силе и для
- есть частотная ПФ. Все остается в силе и для  и
и  .
.
Очевидно, что частотные ПФ  ,
,  и
и  обладают периодическими свойствами (
обладают периодическими свойствами ( ). Это видно и из нижнего рис.13, поскольку одну и ту же выходную последовательность могут вызывать входные сигналы с разными частотами
). Это видно и из нижнего рис.13, поскольку одну и ту же выходную последовательность могут вызывать входные сигналы с разными частотами  .
.

Рисунок 13 – Гармонические сигналы и решетчатые функции
V - преобразование. Билинейные преобразования. Устойчивость и качество импульсных систем

Рисунок 14 – Расположение корней характеристического уравнения
Построим область устойчивости в плоскости комплексной величины  . Воспользуемся методикой D-разбиения и, меняя частоту
. Воспользуемся методикой D-разбиения и, меняя частоту  от
от  до
до  , получим границу
, получим границу  в виде окружности единичного радиуса, внутрь которой попадает левая полуплоскость комплексной величины
в виде окружности единичного радиуса, внутрь которой попадает левая полуплоскость комплексной величины  . Следовательно, для устойчивости, все корни-полюсы замкнутой системы
. Следовательно, для устойчивости, все корни-полюсы замкнутой системы  должны находиться внутри этой окружности.
должны находиться внутри этой окружности.
Итак, для описанных с помощью аппарата Z -преобразования импульсных систем, в силу изменившегося вида области устойчивости и периодичности их ЧХ  , разработанные для непрерывных систем критерии устойчивости (кроме критерия Найквиста и корневого годографа), а так же наиболее эффективные методы коррекции и синтеза (использующие ЛАЧХ и ЛФЧХ) не приемлемы.
, разработанные для непрерывных систем критерии устойчивости (кроме критерия Найквиста и корневого годографа), а так же наиболее эффективные методы коррекции и синтеза (использующие ЛАЧХ и ЛФЧХ) не приемлемы.
Для преодоления этого затруднения используют билинейное v-преобразование, которое отражает окружность единичного радиуса на мнимую ось комплексной величины v, с помощью подстановки
 ;
;  .
.
Физически подстановка означает переход к дифференциальному уравнению заменой в разностном уравнении элементов чистого запаздывания грубой аппроксимацией – одним фазосдвигающим звеном.
Вторая формула для перехода в область псевдочастот 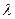 получена из соотношения
получена из соотношения
 ,
,
отметим так же, что:
 .
.
v-домен и домен псевдочастоты 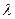 используют редко, поскольку для большинства импульсных и цифровых систем частота дискретизации 1/ T выбирается в 6...10 раз больше частоты среза. В таком случае выполняется условие
используют редко, поскольку для большинства импульсных и цифровых систем частота дискретизации 1/ T выбирается в 6...10 раз больше частоты среза. В таком случае выполняется условие  , вследствие чего в полосе системы псевдочастота
, вследствие чего в полосе системы псевдочастота 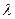 и частота
и частота  практически совпадают. Поэтому обходятся доменом обычных частот, а для переходов используют формулы билинейного преобразования:
практически совпадают. Поэтому обходятся доменом обычных частот, а для переходов используют формулы билинейного преобразования:
 ;
; 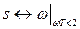 ;
;  .
.
 Резюме:
Резюме:
1. После v-преобразования, используя ПФ  или
или  можно применять обычные (в основном алгебраические) критерии устойчивости, справедливые для непрерывных систем.
можно применять обычные (в основном алгебраические) критерии устойчивости, справедливые для непрерывных систем.
2. После последующего перехода в область псевдочастот (подстановка  ) вид ПФ
) вид ПФ 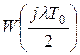 и
и  становится пригоден для применения методов, использующих ЛАЧХ и ЛФЧХ.
становится пригоден для применения методов, использующих ЛАЧХ и ЛФЧХ.
3. Качество импульсной системы может оцениваться построением кривой переходного процесса, что при использовании ПФ  сравнительно легко.
сравнительно легко.
4. Оценку качества в установившихся режимах удобно выполнять нахождением коэффициентов для разложения ошибки в ряд:
 ,
,
которые являются коэффициентами разложения ПФ  в ряд Маклорена по степеням p:
в ряд Маклорена по степеням p:
 ,
,
где  .
.
Понятие о переходном процессе конечной длительности



Рисунок 15 – Модели и переходные процессы
Принципиальным недостатком линейных систем является тот факт, что любой переходный процесс будет иметь бесконечную длительность. Это объясняется тем, что при уменьшении значений сигналов на входах интеграторов пропорционально уменьшается скорость изменения их выходных координат. Т.е. если в линейной астатической системе ошибка становится меньше, то тут же понижается скорость ее компенсации по цепи ООС (рис. 15(1)).
Если же на некоторое время периодически замораживать сигнал в цепи ООС, то скорость изменения выходной координаты интегратора в течение периода "заморозки" уменьшаться не будет, а при правильном подборе периода "заморозки" можно добиться переходного процесса конечной длительности, завершающегося за один или же два цикла (рис. 15 (2 и 3).
Следует отметить, что подобная импульсная система на время "заморозки" сигнала ООС приобретает все достоинства и недостатки не имеющих ОС систем.
Особенности цифрового управления
Одно из самых перспективных направлений создания совершенных автоматических систем связано с применением для целей управления цифровых вычислительных машин (ЦВМ). В сложных цифровых управляющих комплексах цифровые следящие системы (ЦСС) широко используются в качестве устройств связи между объектами управления (ОУ) и ЦВМ. Цифровые следящие системы отличает высокая точность, хорошая помехозащищенность и быстродействие.
ЦВМ по отношению к следящей системе может выполнять функции задающего устройства, сравнивающего и корректирующего устройства. По характеру связи между сле
|
|
|


