Особенности частотных характеристик дискретных систем

 

Работу ЦВМ в контуре управления обеспечивают АЦП (квантователь) и ЦАП (экстраполятор нулевого порядка).

 

Рисунок 21 – Структурная схема

 

На схеме ЦВМ выполняет роль сравнивающего устройства.

Передаточная функция приведенной непрерывной части W₁(Р) W₂(Р)— передаточная функция системы в разомкнутом состоянии. Перейдем в Z-преобразование:

;

 

_;

 

_,

 

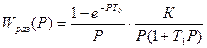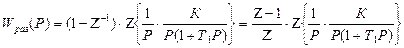Для нахождения Z-изображения непрерывной ПФ по таблицам ее раскладывают на элементарные дроби (т.е. преобразуют к параллельной структуре) и воспользоваться специальными таблицами:

 

 

Передаточная функция системы в замкнутом состоянии

– полностью совпадает с выражением для непрерывных систем. Поэтому требуемые качественные показатели могут быть обеспечены выполнением условий для ЛАЧХ.

При синтезе ЦCC широко используются логарифмические частотные характеристики, которые имеют свои особенности.

1. Построение логарифмических частотных характеристик для всего диапазона частот.

Применение метода ЛАЧХ к расчету ЦСС основано на переходе от Z-преобразований к так называемому V-преобразованию и дальнейшему построению ЛАЧХ для области низких и высоких частот.

(в соответствии с теорией конформных отображений — дробно-линейное преобразование).

Это выражение осуществляет однозначное отображение единичного круга плоскости Z на левую полуплоскость плоскости V, причем контур окружности единичного радиуса на Z-плоскости переходит в мнимую ось на V-плоскости. Для мнимой оси P-плоскости (рис. 14)

 

- диапазон исследуемых частот

_, относительная псевдочастота, а абсолютная псевдочастота
_; Т₀-период дискретности.

Для малых частот и , поэтому при выполнении условия можно в расчетах псевдочастоту 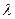заменить действительной частотой .

При изменении псевдочастота изменяется , а комплексная величина V смещается по мнимой оси от до .

V-преобразование частотных характеристик в область псевдочастот 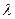позволяет получить ЛАЧХ, которые по виду подобных ЛАЧХ непрерывных систем. Последовательность преобразования следующая:

 

.

 

Однако громоздкость и трудоемкость промежуточных вычислений настолько велики, что сводят на нет преимущества ЛАЧХ при синтезе ЦCC. Для некоторых частных случаев при использовании экстраполяторов нулевого порядка можно формализовать и существенно упростить синтез систем.

Дискретную передаточную функцию разомкнутой системы без цепи коррекции, т.е. D(Z)=1 и при отсутствии запаздывания можно найти по выражению

.

 

Пусть передаточная функция непрерывной части имеет вид:

 

.

 

Разложим эту передаточную функцию на простейшие дроби:

 

, где .

 

Для системы с астатизмом 2-го порядка (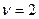) с учетом таблиц Z-преобразования получим:

 

(7)

 

Дискретная передаточная функция для системы с астатизмом 1-го порядка может быть получена из выражения (7), если положить С₁=W(0); C₂=0. Для статической системы .

Для перехода от дискретной передаточной функции к частотной характеристике в выражение для дискретной функции W(Z) следует подставить

Тогда частотная характеристика для системы с астатизмом 2-го порядка преобретает вид:

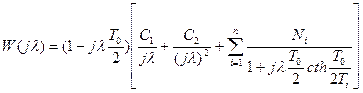, (8)

где cth — гиперболический котангенс.

Если считать, что для m полюсов 1/Т_i передаточной функции непрерывной системы выполняется условие T_i > 2T₀, для е полюсов – условие Т₀>T_i>T₀/2, а для n-m-e полюсов — условие Т_i<T₀/2, то выражение (8) можно представить в виде трех слагаемых

,

 

где .

 

Причем ,

 

;

 

;

 

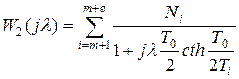при .

 

На основании этих соотношений могут быть построены логарифмические частотные характеристики

.

 

Однако это весьма трудоемко. Построение ЛАЧХ и можно упростить, если его выполнить отдельно для областей низких и высоких частот.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: