 |
Определение структуры и параметров корректирующего устройства (непрерывного и дискретного) и реализация дискретного устройства
|
|
|
|
Возможности коррекции ЦСС шире, чем следящих систем непрерывного действия, можно использовать известные способы коррекции непрерывных систем в двух вариантах – непрерывном и дискретном, а также некоторые новые способы.
1. Непрерывная коррекция
На рис.71 изображены структурные схемы, соответствующие трем основным способам коррекции. При изображении структурных схем экстраполятор нулевого порядка с передаточной функцией  отнесен к непрерывной части системы, которая для удобства представлена двумя звеньями
отнесен к непрерывной части системы, которая для удобства представлена двумя звеньями  и
и  .
.
 |
а)
б)
в)
Рисунок 28 – Способы коррекции
При последовательной коррекции
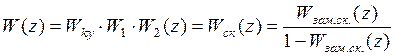 (40)
(40)
Т.к. z – преобразование произведения  не равно произведению z – преобразований
не равно произведению z – преобразований  , то расчет последовательного КУ не является столь простой задачей. Наиболее удобно использование – типовых ЛАЧХ и типовых
, то расчет последовательного КУ не является столь простой задачей. Наиболее удобно использование – типовых ЛАЧХ и типовых  (табл. 1), тогда расчет не будет отличаться от расчета для непрерывных систем:
(табл. 1), тогда расчет не будет отличаться от расчета для непрерывных систем:
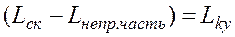 .
.
При коррекции параллельным КУ
 (41)
(41)
удобнее его заменить последовательным КУ.

А при коррекции обратными связями
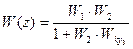
для расчета также удобнее заменить некоторым эквивалентным звеном последовательного типа:
 .
.
2. Дискретная коррекция
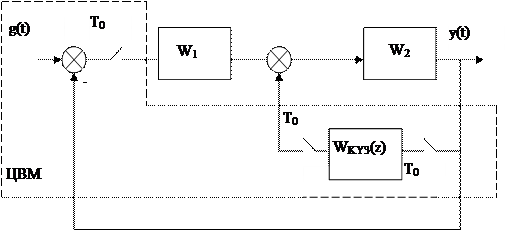
Структурные схемы ЦСС при введении последовательной, параллельной дискретной коррекции, а также при дискретной коррекции обратной связью приведены на рис. 29 (а, б, с)

а)
 |
б)
 |
в)
Рисунок 29 – Структуры при использовании дискретного КУ
Передаточные функции разомкнутой системы при последовательной коррекции
 . (42)
. (42)
При параллельной коррекции
 . (43)
. (43)
|
|
|
При введении обратной связи
 . (44)
. (44)
Выбором дискретного КУ добиваемся совпадения передаточной функции W(z) с желаемой передаточной функцией 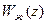 .
.
 (45),
(45),
(46)
Синтез дискретных КУ последовательного и параллельного типа удобно проводить методом ЛАЧХ, используя понятие желаемой ЛАЧХ, главное при этом определить вид желаемых 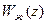 – разомкнутой и
– разомкнутой и  – замкнутой системы. ЦВМ имеют широкие возможности реализации различных физически реализуемых
– замкнутой системы. ЦВМ имеют широкие возможности реализации различных физически реализуемых  , однако следует учитывать определенные ограничения:
, однако следует учитывать определенные ограничения:
1) при последовательной коррекции  в качестве своих нулей (корни числителя) должна иметь все те нули ПФ
в качестве своих нулей (корни числителя) должна иметь все те нули ПФ  , значение которых равно или больше единицы;
, значение которых равно или больше единицы;
2) выражение 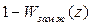 в качестве своих нулей должна содержать все те полюсы
в качестве своих нулей должна содержать все те полюсы  , значения которых равно или больше единицы.
, значения которых равно или больше единицы.
Наиболее сложным с расчетной точки зрения является коррекция обратной связью. В этом случае можно воспользоваться таблицами перехода [4], от выражения  к выражению
к выражению 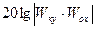 . Вычитая из ЛАЧХ исходной системы ЛАЧХ желаемой получим выражение
. Вычитая из ЛАЧХ исходной системы ЛАЧХ желаемой получим выражение
 и, сделав переход к ЛАЧХ, соответствующей выражению
и, сделав переход к ЛАЧХ, соответствующей выражению 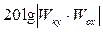 , определим устойчивость внутреннего контура по виду этой ЛАЧХ и структуру и параметры КУ обратной связи.
, определим устойчивость внутреннего контура по виду этой ЛАЧХ и структуру и параметры КУ обратной связи.

 ,
,
где  – ЛАЧХ звеньев, охваченных ОС,
– ЛАЧХ звеньев, охваченных ОС,
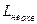 – ЛАЧХ звеньев, не охваченных местной ОС.
– ЛАЧХ звеньев, не охваченных местной ОС.
По виду ЛАЧХ КУ обратной связи определяют структуру и параметры, переходят к z-преобразованию и реализуют с помощью ЭВМ или специального дискретного устройства.
Для составления структурной схемы КУ дискретного типа 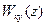 должна быть записана по отрицательным степеням z и ее можно представить в различных формах:
должна быть записана по отрицательным степеням z и ее можно представить в различных формах:
1)  – стандартная форма,
– стандартная форма,
 ; (47)
; (47)
2) 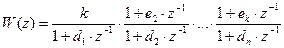 – разложение на сомножители;
– разложение на сомножители;
3) 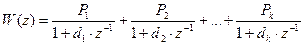 – разложение на элементарные слагаемые дроби,
– разложение на элементарные слагаемые дроби,
где 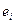 – нули z-передаточной функции;
– нули z-передаточной функции;
 – полюса z-ПФ,
– полюса z-ПФ, 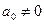 ;
;
 – коэффициент разложения.
– коэффициент разложения.
Таким образом при цифровой коррекции следящих систем предполагается изменение низкочастотного и среднечастотного участка ЛАЧХ, как правило, с уменьшением частоты среза. Известно, что в этом диапазоне системы с ЦВМ и их ЛАЧХ  не отличаются существенно по свойствам от ЛАЧХ
не отличаются существенно по свойствам от ЛАЧХ  непрерывных систем. Поэтому методика синтеза коррекции для цифровых и непрерывных систем едина.
непрерывных систем. Поэтому методика синтеза коррекции для цифровых и непрерывных систем едина.
|
|
|
При определении дискретной коррекции выделяется в четыре этапа:
1. Определение структуры и параметров КУ  по методикам, разработанным для непрерывных систем.
по методикам, разработанным для непрерывных систем.
2. Переход от непрерывной  к эквивалентной дискретной
к эквивалентной дискретной  посредством последовательных переходов по изображениям:
посредством последовательных переходов по изображениям:
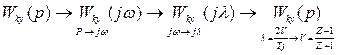 ,
,
или с помощью результирующей формулы билинейного преобразования (формальной подстановки):
 ,
,
где  – период дискретизации ЦВМ.
– период дискретизации ЦВМ.
3. Составление структурной схемы дискретной передаточной функции  , оптимизированной по объему памяти, быстродействию или для контроля промежуточных фазовых координат системы.
, оптимизированной по объему памяти, быстродействию или для контроля промежуточных фазовых координат системы.
4. Написание программы для ЦВМ (периферийный контролер, микро ЭВМ, цифровой сигнальный процессор DSP) или разработка схемы на цифровых микросхемах.
Примечание:
1. Из непрерывной  можно получить бесконечное множество вариантов
можно получить бесконечное множество вариантов  при различных периодах дискретизации ЦВМ.
при различных периодах дискретизации ЦВМ.
2. Обычно частоту дискретизации 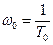 выбирают в (6
выбирают в (6 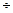 10) раз больше частоты среза
10) раз больше частоты среза 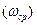 разомкнутой системы. При низких частотах дискретизации качество переходного процесса ухудшается.
разомкнутой системы. При низких частотах дискретизации качество переходного процесса ухудшается.
3. При синтезе  или
или  необходимо, чтобы степень числителя
необходимо, чтобы степень числителя  не была больше степени знаменателя или свободный коэффициент
не была больше степени знаменателя или свободный коэффициент  в знаменателе
в знаменателе  не был равным нулю, иначе невозможно реализовать программу.
не был равным нулю, иначе невозможно реализовать программу.

Общая формула дискретного фильтра
 .
.
4. Если требуется обратный переход от 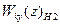 к
к  , следует воспользоваться переходом
, следует воспользоваться переходом
 .
.
Он однозначен при известном периоде дискретности.
Рассмотрим пример синтеза КУ
Исходная система имеет следующую ПФ:
W (p) =  ,
,
T1= 0,05c
K = 420 1/с
T2= 0,003c
T3= 0,001c.
Требования к системе:
1.Максимальная скорость слежения  , максимальное ускорение
, максимальное ускорение 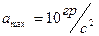 , максимально допустимая ошибка
, максимально допустимая ошибка 
2.Допустимый показатель колебательности M = 1,2.
Ι. Рассчитаем и построим ЛАЧХ исходной непрерывной системы
20lg K = 20lg 420 = 52,46.
Сопрягающие частоты:
lg (ω1 = 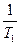 =
=  = 20) = 1,3;
= 20) = 1,3;
lg (ω2 =  ) = 2,52;
) = 2,52;
lg (ω 3 =  ) = 3.
) = 3.
Система с acтатизмом 1-го порядка, наклон в области низких частот на первом участке  до
до  , далее наклоны увеличиваются на
, далее наклоны увеличиваются на  на каждой частоте излома.
на каждой частоте излома.
|
|
|
II. Левее частоты среза ЛАЧХ дискретной системы и ЛАЧХ ее непрерывной части совпадают, а псевдочастота  - с частотой ω. Поэтому формирование желаемой ЛАЧХ левее частоты среза выполним обычными приемами непрерывных систем.
- с частотой ω. Поэтому формирование желаемой ЛАЧХ левее частоты среза выполним обычными приемами непрерывных систем.
1. Формирование области низких частот из требований точности.
По заданным входному сигналу и ошибке построим запретную зону для  и рассчитаем контрольную частоту
и рассчитаем контрольную частоту  .
.
Координата контрольной точки по высоте определяется модулем комплексного коэффициента усиления на частоте  .
.

20lg 600 = 55,6дБ
По этим данным построим контрольную точку Ак и запретную зону из прямых с наклонами  и
и  после частоты ωк = 0,5 1/с (рис. 72).
после частоты ωк = 0,5 1/с (рис. 72).
Желаемая ЛАЧХ должна проходить выше контрольной точки на 3 дБ.
2. Определим необходимое значение коэффициента усиления системы на частоте ω = 1
Ксис. = Dv = 
 .
.
3. На частоте среза наклон желаемой ЛАЧХ должен быть – 20дБ/дек, следовательно, в области низких частот частотная функция будет иметь вид:
Wн.ч.(jω) = 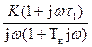
Параметры желаемой ЛАЧХ в низкочастотной области определим в следующем порядке:
Базовая частота 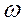 0 =
0 = 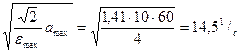 .
.
Постоянная времени, определяющая первый излом:
Tk = 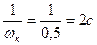 .
.
Для получения заданного показателя колебательности должно выполняться условие
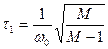

Частоту среза желаемой ЛАЧХ определим через сопрягающие частоты и коэффициент усиления;

4. Для обеспечения заданного показателя колебательности в высокочастотной области должно выполняться неравенство
 ,
,
где Т0 - период дискретности;
 – сумма постоянных времени, меньших чем
– сумма постоянных времени, меньших чем  , т.е. половины периода дискретности.
, т.е. половины периода дискретности.
5. Определим допустимое значение периода дискретности по заданному сигналу. Эквивалентный гармонический сигнал x(t) =  э
э 

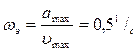 ,
,
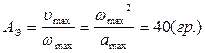 ,
,
T0 =  или
или  .
.
Таким образом Т0 должен быть меньше 0,115. Чем он меньше, тем точнее восстанавливается непрерывный сигнал по дискретному.
С учетом запаздывания на целое число тактов  (требуемого на выполнение расчетов ЦВМ)
(требуемого на выполнение расчетов ЦВМ)
|
|
|
 ,
,
при  ,
,  ;
;
при  ,
,  .
.
Учитывая, что при заданном М = 1,2 сумма  , период дискретности должен быть существенно меньше расчетного. Примем
, период дискретности должен быть существенно меньше расчетного. Примем
Т0 = 0,02c, тогда 
Следовательно T∑ = 0,0154 – 0,01 = 0,0054c – сумма малых постоянных времени.
В области высоких частот ( >
>  =2/To>100) вид желаемой ЛАЧХ непрерывной части может быть произвольным.
=2/To>100) вид желаемой ЛАЧХ непрерывной части может быть произвольным.
6. Важно только, чтобы сумма постоянных времени Т∑ не превышала допустимого значения. Наиболее простые КУ получаются, если сопрягающие частоты желаемой и исходной совпадают, поэтому примем следующие значения малых постоянных времени:
 .
.
Для простоты примем их равными 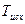 системы.
системы.  .
.
Рассчитаем частоту для дискретной желаемой ЛАЧХ, после которой наклон ЛАЧХ будет нулевым.
 .
.
ЛАЧХ исходной и скорректированной систем приведены на рис.30.

Рисунок 30 – ЛАЧХ исходной и скорректированной системы
Определим структуру и параметры последовательного КУ непрерывного типа:
 ,
,
t1=0,17с
Т1=0,05с
Тк=2с
Ти=0,01с
Т0=0,02.
 - это инерционно форсирующее звено, которое достаточно просто реализуется.
- это инерционно форсирующее звено, которое достаточно просто реализуется.
Перейдем к дискретному КУ. Запишем частотную дискретную функцию КУ:

 .
.
Подставим в полученное выражение  ,
,  .
.
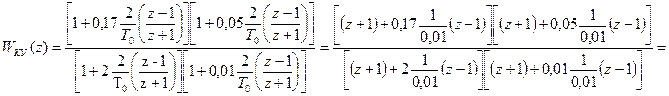

В соответствии с полученным выражением Wку(z) составим структурную схему КУ (рис. 31).

Рисунок 31– Структурная схема дискретного КУ последовательного типа
Дискретное изображение переходной характеристики можно выразить через показатель колебательности М.
 ,
,
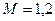

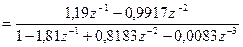
или через  и изображение входного сигнала:
и изображение входного сигнала:
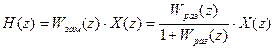 .
.
Значение ординат переходной характеристики в дискретные моменты времени  можно вычислить делением полинома числителя
можно вычислить делением полинома числителя 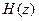 на полином знаменателя. В результате деления получим:
на полином знаменателя. В результате деления получим:


и т.д.
График  представлен на рис. 32.
представлен на рис. 32.
h(t)
 1,19
1,19
Рисунок 32 – Переходной процесс
Влияние квантования по уровню в ЦСУ.
Более полная структурная схема системы с ЦВМ
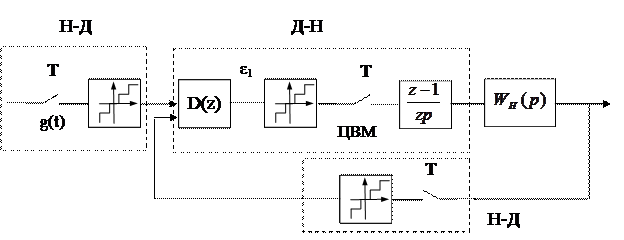 |
Рисунок 33 – Структурная схема системы с ЦВМ
Преобразователи имеют нелинейные элементы. Главный нелинейный фактор вызван преобразованием цифрового кода в непрерывный сигнал в преобразователе Д-Н (ЦАП). Это явление сказывается тем сильнее, чем меньше разрядов имеет преобразователь.
Статическая характеристика выходного устройства ЦВМ представляет собой многоступенчатую релейную характеристику.
 |
Рисунок 34 – Статическая характеристика
Число уровней характеристики m связано с числом двоичных разрядов выходного устройства α зависимостью 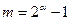 .
.
Зона нечувствительности выходного устройства определяется младшим разрядом. Наибольшее отклонение от линейной зависимости при α=1, что соответствует одноразрядному устройству.
|
|
|
Наличие нелинейности может вызвать периодические режимы в САУ, частота которых жестко связана с частотой выдачи данных ЦВМ. Отметим, что в ЦСУ, синтезированных на основе типовых (желаемых) ЛАЧХ, при соблюдении определенных условий невозможно появление периодических режимов, обусловленных наличием квантования по уровню.
Эти условия получают, используя метод гармонической линеаризации на основе уравнения характеристического вектора:

где  - дискретная частотная функция линейной части,
- дискретная частотная функция линейной части,
 - коэффициент гармонической линеаризации, который зависит не только от амплитуды на входе, но и от фазы входного воздействия и частоты:
- коэффициент гармонической линеаризации, который зависит не только от амплитуды на входе, но и от фазы входного воздействия и частоты:

где 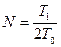 - относительный полупериод,
- относительный полупериод,
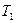 - наибольшая постоянная времени линейной части.
- наибольшая постоянная времени линейной части.
И уравнение приобретает вид:

Частота периодических режимов Ω находится в целочисленном соотношении с частотой выдачи данных ЦВМ  , т.о. все возможные частоты периодических режимов заранее известны.
, т.о. все возможные частоты периодических режимов заранее известны.
Условия существования периодических режимов:
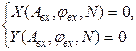
.
Коэффициенты гармонической линеаризации достаточно сложны и поэтому рассчитывать сложно.
Периодические режимы в системе будут невозможны, если АФЧХ линейной части системы, построенная по функции 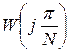 на фиксированных относительных частотах
на фиксированных относительных частотах  не будет заходить в запретную область, которая с запасом может быть представлена в виде сектора с углом
не будет заходить в запретную область, которая с запасом может быть представлена в виде сектора с углом  .
.
Условия невозможности появления периодических режимов можно перенести на ЛАЧХ, строя запретные зоны для фазочастотной характеристики  для исключения периодических режимов
для исключения периодических режимов 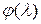 на фиксированных частотах
на фиксированных частотах  не должна заходить в запретные зоны для того же N. Запретные зоны приведены на рис. 35, 36.
не должна заходить в запретные зоны для того же N. Запретные зоны приведены на рис. 35, 36.

Рисунок 35 – Запретная зона для N=1, N=3

Рисунок 36 – Запретная зона для N=3
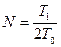 .
.
Запретные зоны строят симметрично относительно 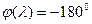 , высота запретной зоны связана с частотой искомых периодических решений:
, высота запретной зоны связана с частотой искомых периодических решений:
 .
.
При N=1 – высота запретной зоны 1800, т.е. ±900 (пунктирная линия), N=2 – высота -900 (±450) и N=3 – высота 600 (±300).
Если фазовая характеристика системы на фиксированной частоте 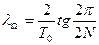 будет находиться в запретной зоне, соответствующей тому же значению N, то возможно существование периодического режима с частотой Ω.
будет находиться в запретной зоне, соответствующей тому же значению N, то возможно существование периодического режима с частотой Ω.
Сопоставление фазовой характеристики 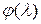 и запретных зон показывает, что периодические режимы при рассматриваемых типах нелинейностей невозможны, если общий коэффициент усиления линейной части выбран на основании формул (98, 101, 102).
и запретных зон показывает, что периодические режимы при рассматриваемых типах нелинейностей невозможны, если общий коэффициент усиления линейной части выбран на основании формул (98, 101, 102).

 ,
,
 .
.
Тогда частотная функция  и уравнение ФЧХ
и уравнение ФЧХ 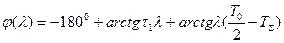 .
.
Для частот левее частоты среза условие незахода в запретную зону ФЧХ:
 .
.
Для N≥3 это условие упрощается и определяется показателем колебательности при М≤2
 .
.
Для N=1 частота периодического режима  , а абсолютная псевдочастота
, а абсолютная псевдочастота  , где запретная зона отсутствует, следовательно, периодических режимов нет.
, где запретная зона отсутствует, следовательно, периодических режимов нет.
Для N=2  , запретная зона на частоте
, запретная зона на частоте  также отсутствует – нет периодического режима.
также отсутствует – нет периодического режима.
Фазовые характеристики в области низких частот для систем статических и с астатизмом первого порядка для типовых ЛАЧХ отстоят от запретной зоны дальше, чем у систем с астатизмом второго порядка.
Поэтому выше приведенное условие невозможности периодических режимов справедливо и для этих режимов.
Цифровые регуляторы
В непрерывных системах широко используются PID-регуляторы, которые представляются идеализированным уравнением

где  , K P - коэффициент усиления пропорционального канала; T Ix - постоянная времени сопрягающего полюса интегрального канала; T Dx - постоянная времени сопрягающего полюса дифференциального канала.
, K P - коэффициент усиления пропорционального канала; T Ix - постоянная времени сопрягающего полюса интегрального канала; T Dx - постоянная времени сопрягающего полюса дифференциального канала.
Для малых периодов дискретизации T уравнение может быть преобразовано в разностное без существенной потери в точности. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников, или метода трапеций.  Используем метод прямоугольников для аппроксимации непрерывного интеграла и запишем PID-закон в дискретном виде:
Используем метод прямоугольников для аппроксимации непрерывного интеграла и запишем PID-закон в дискретном виде:
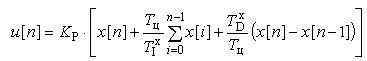
В результате получен нерекуррентный (позиционный) алгоритм управления, который требует сохранения всех предыдущих значений сигнала ошибки x [ i ], и в котором каждый раз заново вычисляется управляющий сигнал u [ n ].
Для реализации программ закона регулирования на ЦВМ более удобным является рекуррентный алгоритм. Он характеризуется тем, что для вычисления текущего значения сигнала u [ n ] используется его предыдущее значение u [ n -1] и поправочный коэффициент, не требующий существенных вычислительных затрат. Определим его:

Перенесем u [ n -1] в правую часть - получим "скоростной" алгоритм для программной реализации регулятора:
(*)
u [ n ] = u [ n -1] + b 0 x [ n ] + b 1 x [ n -1] + b 2 x [ n -2].
 Если для аппроксимации непрерывного интеграла использовать метод трапеций, то разностное уравнение будет иметь вид:
Если для аппроксимации непрерывного интеграла использовать метод трапеций, то разностное уравнение будет иметь вид:

Преобразования, аналогичные вышеизложенным, при получении рекуррентного соотношения (*) выявляют отличия только для коэффициента b 0:
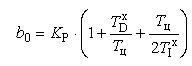
Запишем РУ (*) для изображений в z -форме:
U [ z ] (1- z -1) = (b 0 + b 1 z -1 + b 2 z -1) X [ z ],
и представим его в виде дискретной ПФ:
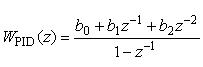
Анализ ее коэффициентов показывает, что:
1. Для исключения статической ошибки, ПФ должна иметь полюс z x=1.
2. Если b 2 = 0, то получим PI-регулятор.
3. Если b 0 = 0, а b 1 = (1 + b 2), то получим PD-регулятор.
|
|
|


