 |
Алгоритмы программ цифровых фильтров
|
|
|
|
Существует три основных алгоритма программной реализации дискретных передаточных функций (z -ПФ) (табл. 2):
Таблица 2 – Основные алгоритмы
| Алгоритм | Требуемое быстродействие | Объём памяти |
 Непосредственный а) с двумя буферами б) с одним буфером
| 24(m+k+1) / T ц | 9m+9k+12 |
| Последовательный
| 52k / T ц | 20k+10 |
| Параллельный
| 50k / T ц | 19k+8 |
Дискретную ПФ можно представить в любой из форм:
где e i - нули z -ПФ; d i - полюса z -ПФ; a 0 - не равно нулю; P i - коэффициенты разложения.
Этим формам представления z -ПФ соответствуют структурные схемы, изображенные на рис. 37.
Рисунок 37 – Структурные схемы
- Разложения (2) и (3) делают параметры z -ПФ независимыми, позволяют контролировать ряд дополнительных фазовых координат: x 1[ n ], x 2[ n ],..., x k-1[ n ]; или y 1[ n ], y 2[ n ],..., y k[ n ] - что удобно при отладке систем.
- Последовательная структура (1) удобна при синтезе дискретной коррекции.
- Параллельная структура (3) удобна для построения цифровых регуляторов.
- Разложение z -ПФ на элементарные дроби позволяет реализовать z -ПФ на параллельно работающих ЦВМ для повышения быстродействия.
Перечисленные факторы определяют выбор алгоритма программы для ЦВМ.
После разложений, каждый из множителей в форме (2) или каждую из элементарных дробей в форме (3) следует представить в стандартной форме (с отрицательными степенями оператора z). Переход к разностным уравнениям будет един. z -ПФ в форме (1) соответствует разностное уравнение (РУ):
по которому и составляется программа. Поскольку текущее значение выходной координаты y [ n ] рассчитывается по предыдущим значениям y [ n -1], y [ n -2], y [ n- k] - данное РУ называется рекурсивным.
Изобразим структурную схему цифрового фильтра для этого уравнения (см. рис. 38). Ее можно преобразовать, объединив два буфера (см. рис. 39). Цепочки элементов z -1 в программах будут соответствовать буферам из ячеек памяти, данные в которых сдвигаются на каждом такте дискретизации. Обе структурные схемы можно составить из простейших блоков программы VisSim.
|
|
|
Алгоритму 1а соответствует структурная схема рис.38.
Рисунок 38 – Структурная схема
Алгоритму 1б соответствует структурная схема рис.39.
Рисунок 39 – Структурная схема
Если выбран последовательный или параллельный алгоритм, то структура каждого множителя или элементарной дроби первого порядка (см. рис. 37) будет иметь более простой вид.
Рисунок 40 – Упрощенная структура
Об эффекте квантования параметров.
ПФ цифрового PID-регулятора имеет три коэффициента b 0, b 1, b 2. Заметим, что только один коэффициент b 1 содержит информацию о таком параметре регулятора, как постоянная времени сопрягающего полюса интегрального канала T Ix. Для объяснения сути эффекта квантования параметров рассмотрим не усугубляющий случай плотного расположения сопрягающих полюсов. Пусть T Ix = 0,1; T Dx = 0,01; при T ц = 0,0003. Рассчитаем коэффициент b 1:
Заметим, что для любой системы отклонение любой постоянной времени в два раза не должно иметь критического значения, однако коэффициенты ПФ, как показано, зависят от параметров отличающихся на порядки, поэтому скажем для отношения T Dx/ T ц, входящего во все коэффициенты числителя ПФ регулятора требуется сохранять мантиссу длиной 5 знакомест (17 двоичных разрядов), поскольку иначе информация о параметре T Ix будет потеряна вследствие округления.
Существуют следующие методы преодоления эффекта квантования параметров при ограниченной длине мантиссы ЦВМ:
1. Развязка параметров посредствам разложения z -ПФ высокого порядка либо на множители, либо на элементарные дроби.
2. Подбор для реализации z -ПФ структурной схемы среди альтернативных, имеющих разные по плотности сетки возможных положений корней в единичной окружности.
|
|
|
Усовершенствованные алгоритмы ПИД-регулятора приводятся в литературе [24, 25].
ВЫВОДЫ
Дискретные САУ способны обеспечить высокую точность (при высокоточных первичных преобразователях). Как устойчивость и динамика, так и точность дискретных САУ зависит от периода дискретности. Поэтому при проектировании дискретных систем основной задачей является правильный выбор периода дискретности, т.е. периода опроса датчиков, при котором соблюдаются условия теоремы Котельникова.
Для САУ с астатизмом первого порядка допустимое значение периода дискретности 
определяется величиной максимального ускорения задающего воздействия, т.е. 
.
,
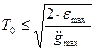где 
- максимально допустимая ошибка системы.
Если задающее воздействие меняется по гармоническому закону 
, то 
.
Для систем с астатизмом второго порядка (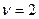
) эти соотношения принимают вид:
и 
,
а требуемый коэффициент усиления системы
и 
на 
.
С учетом нагрузки исполнительного двигателя
,
где 
;
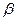- коэффициент преобразования исполнительного двигателя по нагрузке;
- момент нагрузки, приведенной к валу двигателя;
- коэффициент передачи редуктора.
Квантование по времени приводит к частичной потере информации о работе ОУ. Допустимое значение периода дискретности при заданной величине максимальной ошибки определяется соотношением
,
где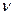 
- порядок астатизма системы;
- максимальное значение 
производной по задающему воздействию 
.
Для того, чтобы период квантования мало сказывался на работе САУ с цифровым УУ (регулятором), рекомендуется [14] период дискретности выбирать из условия
,
где 
наибольшая постоянная времени ОУ;
- запаздывание в системе (ОУ).
По рекомендации Циглера и Никольса [14] период дискретности выбирается из соотношения 
, где
- период критических колебаний ОУ.
Также, как и для непрерывных систем, для повышения точности можно использовать условие инвариантности для и 
.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Теория автоматического управления: учебник для вузов / Л. С. Гольдфарб [и др.]; под ред. А. В. Нетушила. – 2-е изд. перераб. и доп. – Москва: Высшая школа, 1983. – 432 с.
|
|
|
2. Автоматическое регулирование. Теория и элементы систем: учебник для вузов / под ред. Н. Н. Иващенко – 3-е изд. – Москва: Машиностроение, 1973. – 606 с.
3. Анхимюк, В. Л. Теория автоматического управления: учеб. пособие для вузов / В. Л. Анхимюк, О. Ф. Опейко, Н. Н. Михеев – Минск: Дизайн ПРО, 2000. – 352 с.
4. Бесекерский, В. А., Теория автоматического регулирования / В. А. Бесекерский, Е. П. Попов. изд. 3-е, испр. – Москва: Наука, 1975. – 768 с
5. Куропаткин, А. В. Теория автоматического управления: учеб. пособие для электротехн. спец. вузов / А. В. Куропаткин; под ред. Д. В. Васильева. – Москва: Высшая школа, 1973. – 528 с.
6. Справочное пособие по теории систем автоматического регулирования и управления / под общ. ред. Е. А. Санковского. – Минск: Высшая школа, 1973. – 583 с.
7. Топчеев, Ю. И. Атлас для проектирования систем автоматического регулирования: учеб. пособие для вузов / Ю. И. Топчеев. – Москва: Машиностроение, 1989. – 752 с.
8. Кулаков, Г. Т. Инженерные экспресс-методы расчета промышленных систем регулирования: справочное пособие / Г. Т. Кулаков. – Минск: Высшая школа, 1984. – 192 с.
9. Микропроцессорные автоматические системы регулирования. Основы теории и элементы: учеб. пособие / В. В. Солодовников [и др.]; под ред. В. В. Солодовникова. – Москва: Высшая школа, 1991. – 256 с.
10. Наладка автоматических систем и устройств управления технологическими процессами: справочное пособие / под ред. А. С. Клюева. – Москва: Энергия, 1977. – 400 с.
11. Руководство по проектированию систем автоматического управления: учеб. пособие для студентов специальности «Автоматика и теле- механика» / под ред. В. А. Бесекерского. – Москва: Высшая школа, 1983. – 296 с.
12. Проектирование и надежность систем автоматики и телемеханики / А. Д. Горбачев [и др.]: – Минск: Высшая школа, 1981. – 334 с.
13. Основы проектирования следящих систем / под общ. ред. Н. А. Лакоты. – Москва: Машиностроение, 1978. – 391 с.
14. Кулаков, Г. Е. Анализ и синтез систем автоматического регулирования / Г. Е. Кулаков. – Минск: УП Технопринт, 2003. – 125 с.
15. Бесекерский, В. А. Цифровые системы управления / В. А. Бесекерский. – Москва: Наука, 1976. – 320 с.
|
|
|
16. Микропроцессорные системы автоматического управления / под ред. В. А. Бесекерского. – Москва: Машиностроение, 1988. – 365 с.
17. Мееров, В. М. Синтез структур систем автоматического регулирования высокой точности / В. М. Мееров. – Москва: Наука, 1968. – 356 с.
18. Куропаткин, П. В. Оптимальные и адаптивные системы: учеб. пособие для вузов / П. В. Куропаткин. – Москва: Высшая школа, 1980. – 287 с.
19. Коновалов, Г. Ф. Радиоавтоматика: учебник для вузов по специальности «Радиотехника» / Г. Ф. Коновалов. – Москва: Высшая школа, 1990. – 335 с.
20. Лазарева, Т. Я. Основы теории автоматического управления: учеб. пособие / Т. Я. Лазарева, Ю. Ф. Мартемьянов. – Тамбов: Изд-во Тамбовского государственного технологического университета, 2003. – 308 с.
21. Андриевский, Б. Р. Избранные главы теории автоматического управления с примерами на языке Matlab / Б. Р. Андриевский, А. Л. Фрадков. – Санкт-Петербург: Наука, 2000. – 475 с.
22. Клиначев, Н. В. Теория систем автоматического регулирования. Учебно-методический комплекс, 2005. Электронный ресурс.
23. Ким, Д. П. Теория автоматического управления. Т.1. Линейные системы / Д. П. Ким. – Москва: ФИЗМАТЛИТ, 2003. – 288 с.
24. Бажанов, В. USWO – новый способ формирования управления для замкнутых систем автоматического регулирования / В. Бажанов // Современные технологии автоматизации. – 1998. – № 4. – С. 28 – 32.
25. Денисенко, В. ПИД-регуляторы: принципы построения и модификации / В. Денисенко // Современные технологии автоматизации. – 2006. – № 4. – С. 66 – 74; 2007. – № 1. – С. 78 – 86.
|
|
|
