Проектирование дискретных систем с заданными свойствами (расчет периода дискретности, коэффициента усиления, построение ЛАЧХ)

 

Построение ЛАЧХ дискретных систем

При построении ЛАЧХ следящей системы с учетом ЦВМ введем следующие предположения:

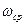
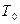
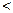
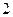1) величина обратная периоду дискретности Т₀, больше половины частоты среза ЛАЧХ непрерывной части системы, т. е. или , это условие приходится выполнять в связи с требованиями по устойчивости и запасу устойчивости;

2) все постоянные времени знаменателя передаточной функции непрерывной части 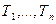можно разделить на две группы. К первой группе отнесем те из них, которым соответствуют сопрягающие частоты, меньшие частоты среза 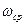(большие постоянные времени). Ко второй группе 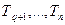отнесем те постоянные времени, которым соответствуют сопрягающие частоты большие, чем частота среза 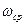(малые постоянные времени), причем для каждой постоянной времени второй группы должно выполниться условие ;

3) постоянным времени 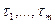(числителя передаточной функции непрерывной части системы) соответствуют сопрягающие частоты меньше, чем частота среза ;

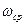4) переход оси нуля децибел асимптотической ЛАЧХ непрерывной части

системы происходит при наклоне -20 .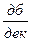

Принятые положения позволяют описать свойства систем в области низких и высоких частот двумя передаточными функциями.

 

,

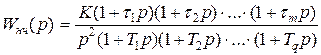где .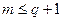

;

 

.

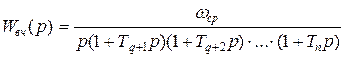1. ЛАЧХ системы с ЦВМ в области низких частот

 

Рассмотрим построение ЛАЧХ для системы, непрерывная часть которой имеет передаточную функцию (ПФ):

 

 

ПФ непрерывной части системы для области низких частот (левее 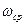) примет вид:

 

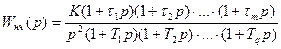
Вследствие условия 4 имеем равенство 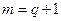. Разложим на простые дроби:

(9)

где 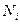— коэффициент разложения,

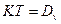— условная добротность по скорости, а .

 

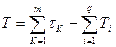Дискретная ПФ в области низких частот:

 

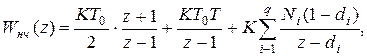
где ;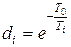

Т₀ – период дискретности.

Перейдем к дискретной частотной характеристике с учетом допущений:

 

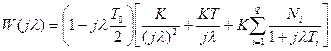(10)

 

Сравнение выражения (9) и (10) показывает, что в низкочастотной области частотная характеристика системы с ЦВМ может быть получена из ПФ непрерывной части подстановкой 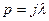и умножением на дополнительный множитель 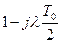. Псевдочастота 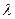в этой области практически совпадает с частотой входного воздействия (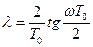, в обл. низких частот ).

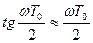Так как было принято, что 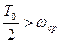, то влияние дополнительного множителя можно не учитывать, т.к. .

Поэтому в низкочастотной области асимптотическая ЛАЧХ системы с ЦВМ практически сливается с ЛАЧХ непрерывной части, причем можно положить 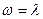, что позволяет значительно упростить построение.

Для формального перехода в область псевдочастот 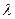достаточно подставить в ПФ непрерывной части системы для области низких частот вместо 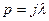и умножить ее на множитель, 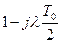для низких частот приближенно равный 1.

Этот вывод непосредственно следует из теоремы Котельникова и Шеннона, устанавливающей эквивалентность непрерывного и дискретного сигналов с точки зрения той информации, которая в них содержится. Существо теоремы состоит в следующем: чтобы восстановить входной сигнал в непрерывной форме из дискретного сигнала, частота квантования 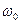должна быть больше удвоенного значения частоты наиболее высокочастотной составляющей входного сигнала 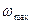или равной ей, т. е. 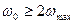или , .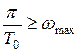

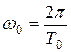Этот случай соответствует такому расположению спектров дискретных сигналов, когда они отстоят друг от друга или примыкают.

Таким образом, для области низких частот получим

 

. (11)

 

2. ЛАЧХ системы с ЦВМ в области высоких частот.

В соответствии с принятыми условиями ПФ непрерывной части для этой области может быть представлена в виде

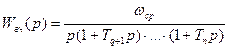, (12)

где .

 

Разложим это выражение на простые дроби:

 

.

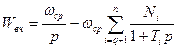Запишем выражение для частотной характеристики:

 

.

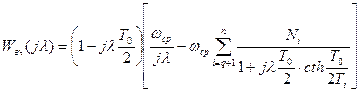Т.к. 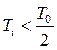, то ,

где cth ─ гиперболический котангенс.

Учитывая, что 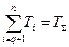, получим

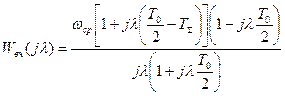. (13)

Это выражение используется для построения псевдочастотной характеристики, причем модуль

 

.

 

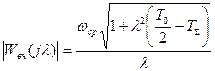Начало ЛАЧХ в высокочастотной области сливается с концом ЛАЧХ низкочастотной области в точке .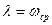

При построении фазочастотной характеристики следует учитывать множитель 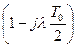, соответствующий неминемально-фазовому звену. Для построения запишем дискретную частотную функцию системы с ЦВМ:

 

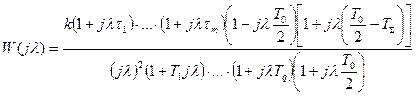. (14)

 

Ей соответствует следующее выражение для фазового сдвига:

 

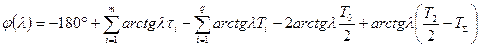. (15)

В районе частоты среза для можно считать с достаточной точностью фазовый сдвиг по соотношению:

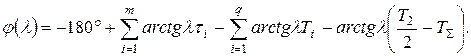(16)

Дополнительный множитель 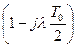приводит к подъему ЛАЧХ на высоких частотах и дает дополнительный фазовый сдвиг в отрицательную сторону, равный 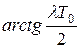. Выражение для 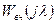зависит от вида ЛАЧХ в области частот больших 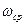непрерывной части системы. Так как для ЛАЧХ вида:

1 (-1-2-1-2…) (рис. 22) и ЛАЧХ вида 2 (-1-2-3…) (рис. 23).

 

 

 

Рисунок 22 – ЛАЧХ вида 1

 

 

Рисунок 23 – ЛАЧХ вида 2 (1-2-3-…)

 

Для таких ЛАЧХ

 

, (17)

 

где 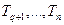— постоянные времени, сопрягающие частоты которых больше частоты 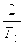, т.е. 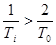, ω_в − коэффициент, определяемый частотой пересечения первой асимптоты высокочастотной ветви ЛАЧХ с осью децибел (может совпадать с ω_ср), а частотная функция

 

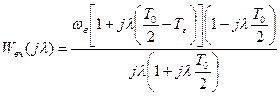. (18)

 

Для ЛАЧХ вида3 (-1-2-3…) (рис. 24) и4 (-2,-3) (рис. 25).

.

 

 

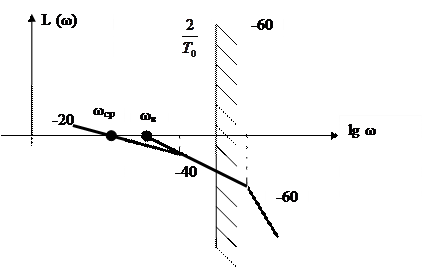
Рисунок 24 – ЛАЧХ вида 3

 

 

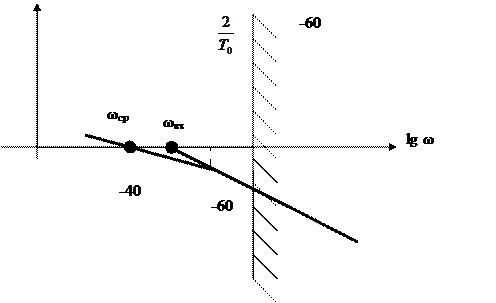
Рисунок 25 – ЛАЧХ вида 4

 

, (19)

 

а частотная функция 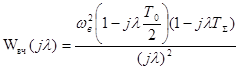(рисунок 24).

 

W_вч (p)= 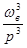(рисунок 25), а частотная функция

 

W_вч (jλ)= (20)

 

Сопряжение низкочастотной и высокочастотной области происходит на частоте λ= , результирующая дискретная частотная функция получается объединением W_нч(jλ) с о W_вч(jλ) в зависимости от того, какой наклон имеет ЛАЧХ на частоте .

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: