 |
Для экономических специальностей заочного отделения
|
|
|
|
Теория вероятностей
Вариант №6
1. Решить задачу, используя классическое определение вероятности и правила комбинаторики.
На полке в случайном порядке расставлено 10 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания (но не обязательно рядом).
2. Решить задачу, используя теоремы сложения и умножения вероятностей. На начальном участке для мотоциклиста-гонщика имеются 3 препятствия, вероятность остановки на каждом из которых равна 0,1. Вероятность остановки на заключительном участке равна 0,7. Какова вероятность того, что мотоциклист доедет до финиша без единой остановки?
3. Решить задачу, используя формулу полной вероятности или формулу Байеса.
В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна 0,9, 0,8 и 0,7. Какой процент отличных деталей выпускает цех в целом?
4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Монету бросают 6 раз. Найти вероятность того, что герб выпадет не менее трех раз.
б) Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 500 случайно отобранных деталей окажется непроверенных: 1) ровно110; 2) от 90 до 115.
5. Найти закон распределения дискретной случайной величины.
Дан перечень возможных значений дискретной величины Х: x 1=1, x 2=3, x 3=5, а также даны математическое ожидание этой величины M[X]=2,2 и ее квадрата M[X2]=6,6. Найти закон распределения случайной величины Х.
6. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
|
|
|
7. Известны математическое ожидание а =3 и среднее квадратичное отклонение s=2 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (4, 8); б) отклонения этой величины от математического ожидания не более, чем на d=3.
Контрольная работа №8
Для экономических специальностей заочного отделения
Теория вероятностей
Вариант №7
1. Решить задачу, используя классическое определение вероятности и правила комбинаторики.
На столе лежат 20 билетов. Какова вероятность того, что 3 наудачу взятых билета имеют номер не больше 5?
2. Решить задачу, используя теоремы сложения и умножения вероятностей. Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты производятся последовательно до наступления события. Определить вероятность того, что понадобится 4 опыта.
3. Решить задачу, используя формулу полной вероятности или формулу Байеса.
У сборщика имеется 16 деталей, изготовленных заводом №1, и 4 детали завода № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом №1.
4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Стрелок производит три выстрела. Вероятность того, что он попадет в цель по крайней мере один раз, равна 0,992. Какова вероятность попадания в цель при одном выстреле?
б) Всхожесть семян определенного сорта растений равна 0,95. Найти вероятность того, что из 500 посаженых семян число проросших будет: 1) ровно 485; 2) не менее 470, но не более 480.
5. Найти закон распределения дискретной случайной величины.
Дискретная случайная величина Х имеет только два возможных значения: x 1 и x 2, причем x 1 < x 2. Вероятность того, что Х примет значение x 1 равно 0,3. Найти закон распределения Х, зная математическое ожидание М[X] = 0,1 и дисперсию D[X] = 1,89.
6. Непрерывная случайная величина Х задана функцией распределения
|
|
|
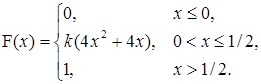
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
7. Известны математическое ожидание а =2 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (6, 12); б) отклонения этой величины от математического ожидания не более, чем на d=3.
Контрольная работа №8
|
|
|


