 |
Для экономических специальностей заочного отделения
|
|
|
|
Теория вероятностей
Вариант №18
1. Решить задачу, используя классическое определение вероятности и правила комбинаторики.
Для уменьшения общего количества игр 10 команд случайным образом разбиты на две равные подгруппы. Определить вероятность того. Что две наиболее сильные команды окажутся в разных подгруппах.
2. Решить задачу, используя теоремы сложения и умножения вероятностей. Вероятность попадания в цель первым стрелком равна 0,8, а вторым – 0,6. Стрелки выстрели одновременно. Какова вероятность того, что один из них попадет в цель, а другой не попадет?
3. Решить задачу, используя формулу полной вероятности или формулу Байеса.
В первой бригаде токарей 2 рабочих имеют первый разряд, 2 рабочих – второй и 5 – четвертый. Во второй бригаде 1 токарь имеет первый разряд, 4 токаря – третий и 2 – четвертый. Из первой бригады во вторую переведен один токарь. Найти вероятность того, что рабочий, наудачу выбранный из нового состава второй бригады, имеет разряд не ниже третьего.
4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Вероятность попадания в цель при одном выстреле из орудия р=0,75. Найти вероятность того, что в цель попадет не менее трех снарядов, если будет сделано 4 выстрела.
б) Вероятность попадания в цель при одном выстреле равна 0,75. Найти вероятность того, что при 80 выстрелах мишень будет поражена: 1) ровно 65 раз; 2) не менее 55 и не более 70 раз.
5. Найти закон распределения дискретной случайной величины.
Дан перечень возможных значений дискретной величины Х: x 1=–2, x 2=–1, x 3=3, а также даны математическое ожидание этой величины M[X]=–0,5 и ее квадрата M[X2]=3,5. Найти закон распределения случайной величины Х.
|
|
|
6. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
7. Известны математическое ожидание а =6 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (1, 8); б) отклонения этой величины от математического ожидания не более, чем на d=6.
Контрольная работа №8
Для экономических специальностей заочного отделения
Теория вероятностей
Вариант №19
1. Решить задачу, используя классическое определение вероятности и правила комбинаторики.
Бросаются две игральные кости. Какова вероятность того, что сумма очков окажется больше 6?
2. Решить задачу, используя теоремы сложения и умножения вероятностей. Бизнесмен забыл последнюю цифру номера телефона своего компаньона и набрал ее наугад. Определить вероятность того, что ему придется набирать номер не более трех раз, если известно, что последняя цифра была четной.
3. Решить задачу, используя формулу полной вероятности или формулу Байеса.
Три стрелка производят по одному выстрелу по одной и той же мишени. Вероятность попадания для первого стрелка равна 0,6, для второго – 0,5, для третьего – 0,4. В результате произведенных выстрелов в мишени оказалось две пробоины. Найти вероятность того, что в мишень попали второй и третий стрелки.
4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Найти вероятность того, что при 5 испытаниях событие наступит ровно 3 раза, если вероятность его появления в каждом испытании равна 0,3.
б) Монету бросают 450 раз. Найти вероятность того, что герб появится: 1) ровно 200 раз; 2) от 220 до 250 раз.
5. Найти закон распределения дискретной случайной величины.
Дискретная случайная величина Х имеет только два возможных значения: x 1 и x 2, причем x 1 < x 2. Вероятность того. что Х примет значение x 1 равно 0,6. Найти закон распределения Х, зная математическое ожидание М[X] = 0,6 и дисперсию D[X] = 3,84.
|
|
|
6. Непрерывная случайная величина Х задана функцией распределения
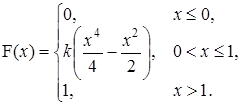
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
7. Известны математическое ожидание а =5 и среднее квадратичное отклонение s=2 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 6); б) отклонения этой величины от математического ожидания не более, чем на d=5.
Контрольная работа №8
|
|
|


