 |
Винтовых пружин с малым шагом витков
|
|
|
|
Винтовая пружина представляет собой тонкий стержень, чаще всего круглого сечения, ось которого является винтовой линией. Винтовые пружины применяются в вагонных рессорах и различных деталях машин и механизмов. Для пружин с малым шагом витков (рис.15а) соблюдается условие
(1)
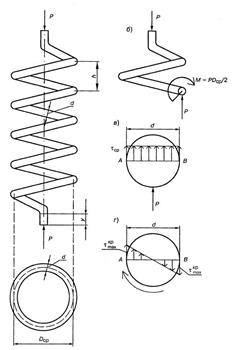
рис. 15
Здесь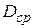 
- средний диаметр пружины, т.е. диаметр цилиндра, на котором лежит винтовая ось пружины. Таким образом, в этом случае, можно приближенно считать, что плоскость витка горизонтальна. Несмотря на сравнительную сложность формы оси, нетрудно вывести формулы для приближенного расчета пружин с малым шагом. При действии сил, направленных по оси пружины и растягивающих или сжимающих ее, стержень пружины в основном испытывает кручение.
Проведем в каком-либо месте разрез стержня пружины вертикальной плоскостью, проходящей через ось пружины (рис.15б) и отбросим нижнюю часть. При условии (1) сечение приближенно можно считать не эллипсом, а кругом.
Действие отброшенной части на верхнюю сводится к силе Р, направленной вверх по оси пружины. При параллельном переносе силы Р в центр сечения стержня (рис.15б) присоединится крутящая пара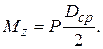 
Таким образом, в сечении пружины возникают два внутренних силовых фактора: поперечная сила Q=Р и крутящий момент 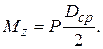Оба эти фактора вызывают в сечении касательные напряжения. Наибольшие напряжения от кручения (у контура сечения) будут равны (рис.15г)
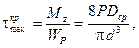(2)
где d – диаметр стержня пружины.
Напряжения от поперечной силы имеют наибольшую величину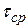 
вдоль горизонтального диаметра АВ сечения, где они направлены вертикально. По формуле Журавского (рис.15в)
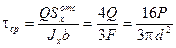. (3)
Внутренняя точка А диаметра является опасной точкой сечения, так как здесь напряжения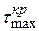 
и 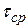совпадают по направлению и складываются. Расчетное напряжение будет
|
|
|
(4)
При малом отношении 
можно вторым членом в скобках пренебречь по сравнению с единицей, т.е. рассчитывать пружину на одно кручение.
Если же отношение не мало (например, в вагонных рессорах и других тяжелых пружинах), то влияние поперечной силы на напряжения значительно и должно учитываться. Кроме того, в этом случае существенно сказывается влияние кривизны стержня пружины, вследствие которой напряжение от кручения у внутренней точки А сечения оказывается больше, чем у наружной точки В. Ввиду этого в правую часть формулы (4) вместо выражения, стоящего в скобках, лучше ввести коэффициент К, учитывающий одновременно влияние поперечной силы и кривизны стержня:
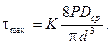(5)
Этот коэффициент можно вычислять по формуле
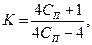(6)
где 
- геометрический параметр пружины.
На практике нужно уметь вычислять удлинение или осадку пружины от растягивающих или сжимающих ее сил. Влияние поперечной силы на удлинение невелико, поэтому обычно принимается в расчет влияние кручения витков.
На рис.16 показан бесконечно малый элемент проволоки пружины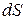 
, находящейся в условиях кручения. Правое сечение поворачивается на угол
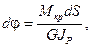
а все точки на оси перемещаются на величину
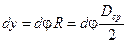. (7)
Суммируя эти перемещения за счет закручивания длины проволоки, получим полное сокращение расстояния между торцами пружины
(8)
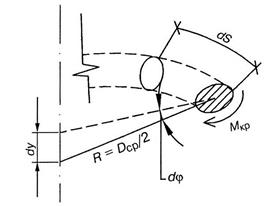
рис. 16
Условие прочности пружины
(9)
Так как пружины должны давать достаточно большие упругие удлинения, то они изготовляются из закаленной стали с очень высоким пределом пропорциональности. Допускаемое касательное напряжение 
колеблется при статической нагрузке от 350 МПа до 500 МПа, а для особо прочных специальных сталей – и выше. При переменной нагрузке допускаемое напряжение значительно снижается (на 30-65 %).
Клапанная пружина находится под действием сжимающих сил, меняющихся по величине (рис.17) от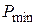 
(предварительное поджатие) до 
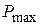(в конце рабочего хода).
|
|
|
Касательное напряжение в опасной точке А также меняется по формуле (5) от 
.
Прочность пружины при этом понижается в результате возникновения микротрещин и их постепенного развития.
Явление понижения прочности материалов при циклических напряжениях называется усталостью материала. Способность материала сопротивляться усталостному разрушению называется выносливостью.
Расчет на выносливость сводится к вычислению запаса усталостной прочности n и сравнению его с нормативным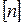 
. Должно выполняться условие 
.
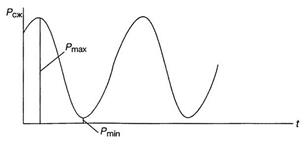
рис. 17
На рис. 18 показана зависимость циклического напряжения от времени и обозначены основные характеристики цикла:
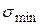- минимальное напряжение цикла;
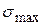- максимальное напряжение;
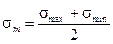- среднее напряжение;
- амплитудное напряжение.
Для каждого цикла можно подсчитать коэффициент асимметрии цикла
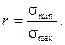
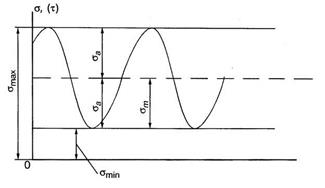
рис. 18
В частных случаях нагружение может быть симметричным пульсирующим и статическим (стационарным) (рис. 19).
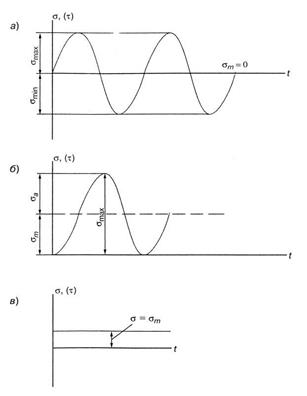
рис. 19
Основные характеристики этих циклов следующие:
для симметричного цикла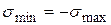 
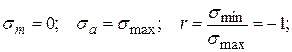
для пульсирующего цикла 
для статического (стационарного) 
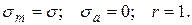
Максимальное напряжение цикла, при котором стандартный образец выдерживает бесконечное число циклов нагружений не разрушаясь, называется пределом выносливости материала. Для симметричного цикла предел выносливости при чистом изгибе обозначается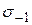 
, а при чистом кручении - 
.
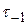Предел выносливости устанавливается по экспериментальной кривой усталости (рис. 20) – нагружения при чистом изгибе образца с вращением.
Для углеродистой стали циклов нагружения 
и напряжение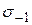
при принимают за предел выносливости.
На предел выносливости влияют следующие факторы:
- концентрация напряжений в связи с наличием отверстий выточек, надрезов, уступов и т.д.,
- размеры детали (масштабный фактор),
- качество поверхности детали,
- асимметрия цикла напряжений.
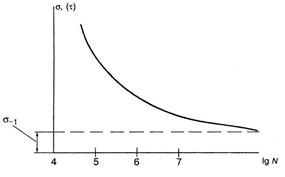
рис. 20
Эти факторы снижают предел выносливости. Их влияние учитывают соответствующими коэффициентами, определяемыми экспериментально:
- коэффициенты концентрации напряжений при растяжении и кручении;
|
|
|
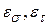- коэффициенты масштабного фактора (размеры детали);
- коэффициент качества поверхности.
Факторы влияния на предел выносливости (концентрация напряжений, размеры детали, состояние поверхности) устанавливают экспериментально.
Коэффициент концентрации напряжений определяют как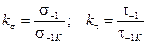 
,
где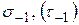 
- предел выносливости серии образцов при симметричном цикле без концентрации напряжений (соответственно при изгибе и кручении);
- то же с концентратором.
Масштабный фактор влияния определяют отношением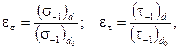 
где в числителе – пределы выносливости детали, а в знаменателе – опытного образца малого размера.
Обычно принимают 
. Влияние качества обработки поверхности учитывают коэффициентом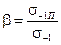 
,
где 
- пределы выносливости данной детали и полированного образца.
Названные факторы (коэффициенты) проводятся в соответствующих справочниках. Их общее влияние можно выразить комплексным коэффициентом 
. (10)
При выбранных коэффициентах влияния запас прочности по усталостному разрушению определяется как
. (11)
Здесь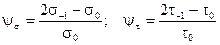 
, (12)
где 
- предел выносливости при пульсирующем цикле 
.
Запас статической прочности
, (13)
где 
- пределы текучести при кручении и растяжении (изгибе) соответственно.
Следует обратить внимание, что при действии только нормальных напряжений (например, изгиб) или только касательных (например, кручение) коэффициенты берут с соответствующими индексами. Если имеют место те и другие, то коэффициент запаса прочности на выносливость при циклическом нагружении (например, изгиб и кручение вала) определяется формулой
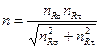. (14)
При статическом нагружении
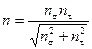, (15)
что следует из рассмотрения плоского напряженного состояния.
Запас прочности по выносливости можно определить с помощью диаграммы усталостной прочности в координатах 
. Если экспериментально определять пределы выносливости для различных видов циклов и откладывать графически соответствующие точки с координатами (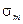
, 
), то (рис.21) можно построить предельную линию (АВ) – диаграмму усталостной прочности при несимметричных циклах. Если при заданном цикле определено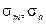 
- рабочая точка и на графике она лежит ниже предельной кривой, то деталь работает неограниченно долго.
|
|
|
Для практического использования диаграмму схематизируют до ломанной прямой, координаты которой указаны на рис. 22. Диаграмма изображена в координатах касательных напряжений (кручение).
Здесь уравнение линии АВ 
уравнение линии ВС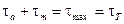 
.
Изменение напряжений в расчетной точке пружины фиксируется на диаграмме рабочей точкой М. Отношение отрезка от начала координат до предельной линии (ON) к длине отрезка ОМ от начала координат до рабочей точки М есть запас прочности по выносливости, т.е.
. (16)
рис. 22
В точке N имеем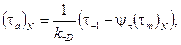 
т.к. 
то из этих соотношений следует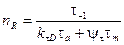 
, (17)
что соответствует (11).
Если предельно состояние зависит не от выносливости (усталости), а от текучести материала (линия ВС), то запас прочности определяется пределом
текучести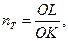 
(18)
что соответствует (13).
При расчете необходимо сравнить попарно запасы прочности (11), (13) или (14), (15) аналитического расчета и графического (16), (18). Принимается меньший из них.
Пример задачи № 10
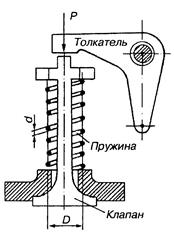
Для цилиндрической клапанной пружины (рис.23) двигателя внутреннего сгорания определить коэффициент запаса прочности аналитически (по формуле С.В. Серенсена и Р.С. Кинасошвили) и проверить его графически по диаграмме предельных амплитуд, построенной строго в масштабе. Средний диаметр пружины D = 40 мм, диаметр проволоки пружины d = 4 мм. Сила, сжимающая пружину в момент открытия клапана 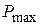=240 Н, в момент закрытия клапана 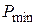= 96 Н. Материал проволоки пружины – хромованадиевая сталь с механическими характеристиками: предел текучести 
= 900 МПа, предел выносливости при симметричном цикле 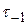=480 МПа, предел выносливости при отнулевом (пульсирующем) цикле 
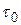= 720 МПа. Для проволоки пружины эффективный коэффициент концентрации напряжений 
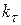=1,05, коэффициент влияния качества обработки поверхности = 0,84, коэффициент влияния абсолютных размеров поперечного сечения 
= 0,96.
Решение
1. Определение максимального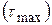 
и минимального 
напряжений
в проволоке пружины и вычисление коэффициента асимметрии цикла R
|
|
|
