 |
Основные теоретические сведения
|
|
|
|
Метод начальных параметров
Уравнение изогнутой оси по методу начальных параметров в общем виде имеет следующий вид:

 , (1.1)
, (1.1)
где  – жесткость балки;
– жесткость балки;  – начальный и текущий прогибы;
– начальный и текущий прогибы; 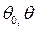 – начальный и текущий углы поворота;
– начальный и текущий углы поворота; 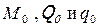 – усилия в начале координат;
– усилия в начале координат;  – усилия в произвольном месте балки;
– усилия в произвольном месте балки; 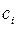 – координата приложения сосредоточенных усилий или координата начала распределенной нагрузки.
– координата приложения сосредоточенных усилий или координата начала распределенной нагрузки.
Уравнение углов поворота сечений получается дифференцированием.

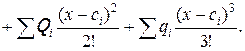 (1.2)
(1.2)
При выводе уравнений (1.1) и (1.2) считали, что распределенная нагрузка действует от точки x = c4 до конца балки. Если такая нагрузка действует на участке от x = c4 до x = c5 , то ее можно рассматривать как результат наложения двух нагрузок, показанных на рис. 1.2. В уравнения обязательно добавляются слагаемые, учитывающие действие компенсирующей нагрузки (см. пример 2).
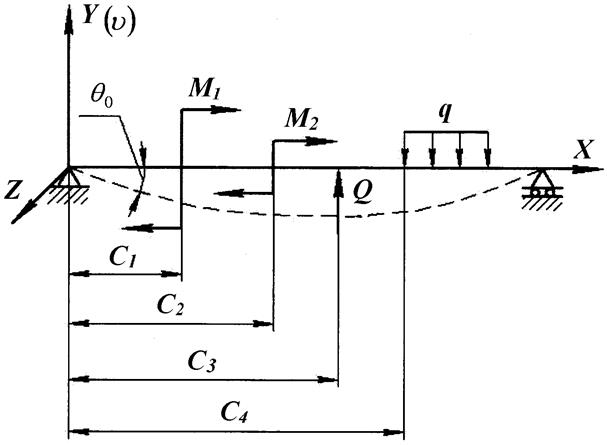
Рис. 1.1.

Рис. 1.2.
Порядок составления уравнения
1. Выбираем систему координат. Система координат правая – начало координат на левом краю балки.
2. Записываем граничные условия в начале координат для перемещений и усилий.
3. Записываем уравнение (1.1) с учетом известных перемещений и усилий в начале координат (п. 2).
4. Определяем, если это необходимо, неизвестные перемещения в начале координат из граничных условий, используя уравнение (1.1) (п. 3).;
5. Окончательно записываем уравнение изогнутой оси балки, подставив в него перемещения в начале координат.
Правило знаков
1. Ось  направлена вверх, поэтому положительный прогиб откладываем вверх, отрицательный вниз.
направлена вверх, поэтому положительный прогиб откладываем вверх, отрицательный вниз.
2. Знаки усилий определяем по правилу, принятому при построении эпюр Q и M.
Примеры
1. Консольная балка

| 
| 
|
| 
| |

| ||

| ||
| ||

|
 ;
;
|
|
|
 .
.
2. Двухопорная балка

| 
| 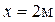
|
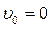
| 
| |

| 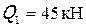
| |

| 
| |
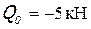
| ||

|
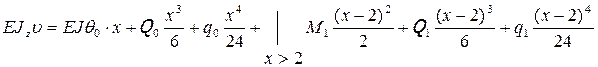 ;
;
 .
.
Определяем  из условия: x = 2 м,
из условия: x = 2 м, 
 ;
;
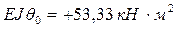 .
.
Окончательно
 .
.
Правило Мора-Верещагина (графический способ вычисления
Интеграла Мора)
Кроме метода начальных параметров существует эффективный универсальный метод определения перемещений в балках, рамах и упругих конструкциях произвольной конфигурации – метод Мора. Упругое перемещение  (либо прогиб
(либо прогиб  , либо угол поворота сечения
, либо угол поворота сечения  ) определяется по формуле:
) определяется по формуле:
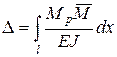 , (1.3)
, (1.3)
где  – изгибающий момент от заданной нагрузки;
– изгибающий момент от заданной нагрузки; 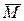 – изгибающий момент от единичной силы, приложенной в той точке, в которой определяется перемещение.
– изгибающий момент от единичной силы, приложенной в той точке, в которой определяется перемещение.
Упрощение операций интегрирования возможно для конструкций с прямолинейной осью постоянной жесткости и основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассматривая эту процедуру применительно к участку балки, преобразуем интеграл Мора с учетом этой особенности. На рис. 1.3 сверху показан участок балки с эпюрой 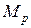 общего вида, а внизу эпюра
общего вида, а внизу эпюра 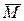 , представляющая собой линейную функцию. В результате несложного расчета (подробности смотри в учебнике) установлено, что интеграл произведения двух функций
, представляющая собой линейную функцию. В результате несложного расчета (подробности смотри в учебнике) установлено, что интеграл произведения двух функций 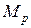 и
и 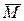 численно равен площади эпюры
численно равен площади эпюры 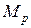 , умноженной на величину момента, взятого с эпюры
, умноженной на величину момента, взятого с эпюры 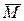 в сечении, соответствующем центру тяжести эпюры
в сечении, соответствующем центру тяжести эпюры 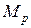 .
.
 . (1.4)
. (1.4)

Рис. 1.3.
Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид
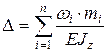 , (1.5)
, (1.5)
где  – площадь эпюры моментов от внешней нагрузки (грузовой эпюры);
– площадь эпюры моментов от внешней нагрузки (грузовой эпюры);  – ордината единичной эпюры под центром тяжести грузовой эпюры;
– ордината единичной эпюры под центром тяжести грузовой эпюры;  – число участков по длине балки.
– число участков по длине балки.
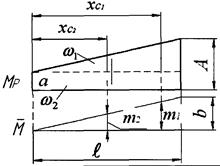
При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.
|
|
|
Таблица 1.1
Эпюры  и и 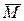
| Площадь грузовой опоры | Ордината единичной
эпюры  ,
координата центра
тяжести ,
координата центра
тяжести 
|

| 
| 
|

| 
| 
|

| 
| 
|
Окончание таблицы 1.1
Эпюры  и и 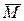
| Площадь грузовой опоры | Ордината единичной
эпюры  ,
координата центра
тяжести ,
координата центра
тяжести 
|

| 
| 
|

| 
| 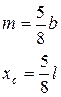
|
| 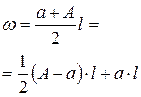
| 
|
Примечания: 1. Все кривые в табл. 1.1 – квадратные параболы. 2. При «перемножении» эпюр одного знака их произведение положительно. 3. При «перемножении» эпюр разных знаков их произведение отрицательно.
В случае, если эпюра  тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.
тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.
Рассмотрим на примере расчетной схемы, показанной на рис. 1.4, порядок решения задач при определении перемещения с помощью правила Мора-Верещагина. Определим прогиб в точке  .
.
Чтобы построить эпюры  и
и  , можно не определять опорные реакции: достаточно сосчитать момент на опоре
, можно не определять опорные реакции: достаточно сосчитать момент на опоре  от нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значение M на опоре B с нулем на опоре A.
от нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значение M на опоре B с нулем на опоре A.
В соответствии с формулой (1.5)
 .
.

Рис. 1.4.
Метод сил
Данный метод применяется для расчета статически неопределимых конструкций. В качестве неизвестных принимаются реакции опор или внутренние усилия. Порядок расчета рассмотрим на примере простой балки, степень статической неопределимости которой равна единице (рис. 1.5,а).

Рис. 1.5.
Отбрасываем «лишнюю» связь, превращая тем самым заданную балку в статически определимую. Полученная балка называется основной системой. В качестве «лишней» неизвестной может быть взята любая, не равная нулю реакция (реакция опоры  или момент в заделке MA), или изгибающий момент в любом поперечном сечении. Для рассматриваемой балки самое простое – убрать правую опору. Тогда «лишняя» неизвестная – реакция этой опоры
или момент в заделке MA), или изгибающий момент в любом поперечном сечении. Для рассматриваемой балки самое простое – убрать правую опору. Тогда «лишняя» неизвестная – реакция этой опоры  .
.
Загружаем основную систему заданной внешней нагрузкой и «лишней» неизвестной. Получим так называемую эквивалентную систему (рис. 1.5,б).
Составляем условие совместности деформаций. Оно состоит в отрицании вертикального перемещения точки В:
|
|
|
 , (1.6)
, (1.6)
где  – перемещение точки приложения силы X1 по направлению ее действия;
– перемещение точки приложения силы X1 по направлению ее действия;  – перемещение точки приложения силы X1, вызванное действием этой силы (рис. 1.5,г);
– перемещение точки приложения силы X1, вызванное действием этой силы (рис. 1.5,г);  – перемещение точки приложения силы X1, вызванное действием внешней нагрузки (рис. 1.5,в).
– перемещение точки приложения силы X1, вызванное действием внешней нагрузки (рис. 1.5,в).
Перемещение от неизвестной X1 удобно представить в виде:
 ,
,
где  – перемещение, вызванное действием единичной силы
– перемещение, вызванное действием единичной силы  , приложенной в направлении действия силы X1 по направлению ее действия (рис. 1.5,д). Таким образом, уравнение (1.6) принимает вид:
, приложенной в направлении действия силы X1 по направлению ее действия (рис. 1.5,д). Таким образом, уравнение (1.6) принимает вид:
 . (1.7)
. (1.7)
Здесь уравнение совместности деформаций записано в стандартной (канонической) форме. Оно имеет такую форму вне зависимости от того, какая принята «лишняя» неизвестная – сила или момент.
Найдем коэффициенты уравнения (1.7) по правилу Верещагина (рис. 1.5,е,ж).
 . (1.8)
. (1.8)
В нашем случае количество участков n=1.
 ,
,
где  – площадь эпюры
– площадь эпюры  ;
;  – ордината под центром тяжести указанной площади, измеренная на той же эпюре
– ордината под центром тяжести указанной площади, измеренная на той же эпюре  . Мы «перемножили» эпюру саму на себя.
. Мы «перемножили» эпюру саму на себя.
 .
.
После подстановки значений  и
и  в (1.7) получим
в (1.7) получим
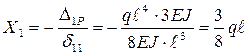 .
.
Далее строим эпюры Q и M так же, как мы это делали при расчете статически определимых балок (рис. 1.6). Задача решена, статическая неопределенность раскрыта.
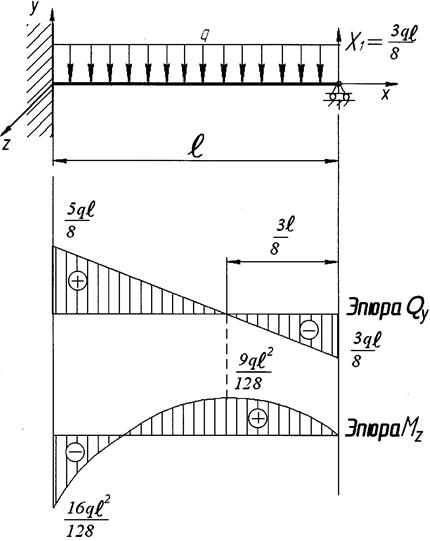
Рис. 1.6.
Для балки или рамы, которые имеют степень статической неопределимости более единицы, условие совместности деформаций представляет собой систему уравнений, которую записывают в каноническом виде.
Например, для дважды статически неопределимой балки она имеет вид:
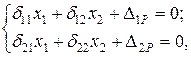 (1.9)
(1.9)
где  – перемещение от единичной нагрузки, приложенной в точке приложения силы
– перемещение от единичной нагрузки, приложенной в точке приложения силы 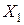 , в направлении действия силы
, в направлении действия силы 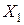 ;
;  – перемещение от единичной нагрузки, приложенной в точке приложения силы
– перемещение от единичной нагрузки, приложенной в точке приложения силы 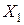 , в направлении действия силы
, в направлении действия силы  ;
;  – перемещение от единичной нагрузки, приложенной в точке приложения силы
– перемещение от единичной нагрузки, приложенной в точке приложения силы  , в направлении действия силы
, в направлении действия силы 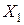 ;
;  – перемещение от единичной нагрузки, приложенной в точке приложения силы
– перемещение от единичной нагрузки, приложенной в точке приложения силы  , в направлении действия силы
, в направлении действия силы  . Установлено, что
. Установлено, что  =
= 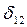 ,
,  – перемещение от внешней нагрузки в направлении действия силы
– перемещение от внешней нагрузки в направлении действия силы 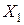 ;
;  – перемещение от внешней нагрузки в направлении действия силы
– перемещение от внешней нагрузки в направлении действия силы  .
.
|
|
|
|
|
|


