Особенности построения эпюр внутренних усилий в рамах

 

Рама – это стержневая система, состоящая из двух и более стержней, лежащих в одной плоскости и жестко соединенных в местах стыков.

Порядок построения эпюр внутренних усилий (эпюра Q, эпюра М) аналогичен тому, как это делается для балок с несколькими участками и прямолинейной осью (см. РГР №4), с той лишь разницей, что оси отдельных участков стержней на раме не лежат на одной линии. В этой связи правило знаков для Q и M, принятое при построении эпюр в балках, неудобно. Для удобства построения эпюр внутренних усилий в рамах принимаем правило построения эпюр внутренних усилий на сжатом волокне стержней, составляющих раму.

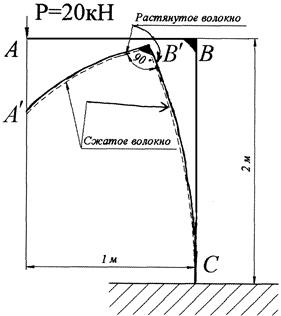
Рассмотрим раму, состоящую из двух стержней AB и BC с опорой в точке C в виде жесткой заделки (рис. 1.7). Стержни AB и BC жестко соединены в точке B (в процессе деформации под действием внешней нагрузки 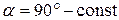). Построим эпюру внутренних изгибающих моментов для такой стержневой системы.

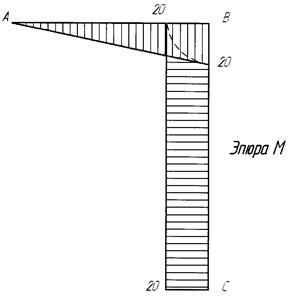
Для построения эпюры M (рис. 1.8) необходимо вычислить значения внутренних изгибающих моментов на левой и правой границах каждого из стержней, составляющих раму. Это можно сделать путем составления уравнения внутренних изгибающих моментов для участков рамы, с последующей подстановкой в них координат точек, где вычисляется внутреннее усилие, или путем непосредственного определения значений внутренних усилий в заданных точках. Двигаясь со свободного края рамы (стержня AB) вычислим моменты в точках A и B. Соответственно М_А = 0, М_В = 20 кНм. В стержне AB при действии силы P будут сжаты нижние волокна, поэтому значения моментов откладываем вниз от оси стержня AB. Завершаем построение эпюры M на стержне AB, соединив точки и прямой линией. Далее рассматриваем стержень BC. Все нагрузки, приложенные к стержню AB, приводим к точке B. Анализ напряженного состояния стержня BC показывает, что он нагружен сжимающей силой и изгибающим моментом .

 

Рис. 1.7.	Рис. 1.8.

 

 

Таким образом, на стыке стержней АВ и BC внутренний изгибающий момент будет равен 20 кНм. Так как никаких других изгибающих нагрузок на стержень ВС не действует, внутренний изгибающий момент будет постоянным на участке ВС. Откладываем значение 20 кНм слева от оси стержня BC в точки B и C и соединяем эти точки прямой линией; слева – потому что волокна слева от оси стержня будут сжаты. Так как сжимающая нагрузка Р, приложенная к стержню ВС, не является определяющей, то на этапе расчета на изгиб рамы ею пренебрегаем. Она будет учтена при проверочном расчете, который выходит за рамки задания.

 

 

ПРИМЕРЫ РАСЧЕТА

 

Часть I. расчет на прочность статически

Неопределимой балки

Задание

 

Для балки, выбранной на рис. 1.9, выполнить следующие расчеты:

1. Раскрыть статическую неопределимость, используя метод сил;

2. Построить эпюры поперечных сил Q. и изгибающих моментов М;

3. Из условия прочности по нормальным напряжениям при изгибе подобрать сечение двутаврового профиля по допускаемым напряжениям . Линейные размеры и величины нагрузок взять в табл. 1.2.

Исходные данные

 

Расчетная схема балки приведена на рис. 1.10,а.

 

Решение

 

1. Определение степени статической неопределимости балки.

Как известно, плоская статически определимая система содержит три связи. При этом защемление дает три связи, шарнирно неподвижная опора 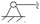– две связи, а шарнирно подвижная 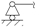– одну связь. Поэтому степень статической неопределимости плоской стержневой системы N определяется по формуле

N= С – 3, (1.10)

где С – общее число связей; N – степень статической неопределимости системы.

Таблица 1.2

№ стро-ки	№ схемы	Балка	№ схемы	Рама
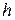
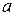
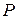
м	кН	кН/м	кНм		м	кН	кН/м	кНм
		1,0	1,5	0,5					1,0	2,0	0,4		-	-
		1,5	2,0	1,0					1,2	2,2	0,5	-		-
		2,0	2,5	1,5					1,4	2,4	0,6	-	-
		2,5	3,0	2,0					1,6	2,6	0,7		-	-
		3,0	2,5	2,5					1,8	2,8	0,8	-		-
		2,5	2,0	3,0					2,0	3,0	0,9	-	-
		2,0	1,5	2,5					2,2	3,2	0,8		-	-
		1,5	1,0	2,0					2,4	3,4	0,7	-		-
		1,0	0,5	1,5					2,6	3,6	0,6	-	-
		0,5	1,0	1,0					2,8	3,8	0,5		-	-
	е	г	д	в	д	е	а	е	а	б	г	е	е	е

 

Рис. 1.9.

Рис. 1.10.

В нашем случае С = 2+1+1, так как имеем две шарнирно подвижных и одну шарнирно неподвижную опору. На схеме (рис. 1.10,а) для каждой опоры проставлено количество связей. Поэтому, используя формулу (1.10), получим N = 4 - 3 =1. Следовательно, в нашем случае балка один раз статически неопределима.

2. Выбираем основную систему (о.с), т.е. статически определимую, геометрически неизменяемую систему, которая получается из исходной статически неопределимой путем отбрасывания «лишних» связей. В нашем случае отбрасываем опору А и полученная о.с. показана на схеме (рис. 1.10,б). Такая схема удобна тем, что в процессе построения эпюр 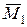и не нужно определять реакции опор, так как эпюры могут быть построены и без определения реакций опор. В некоторых случаях такой подход к решению задачи невозможен и при построении эпюр 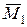и , предварительно необходимо определять реакции опор.

3. Загружаем о.с. внешней нагрузкой и «лишней» неизвестной (рис. 1.10,в).

4. Составляем систему канонических уравнений метода сил.

Так как рассматриваемая балка один раз статически неопределима, то для нее записывается одно уравнение (1.7):

,

откуда

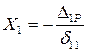, (1.11)

где –перемещение по линии действия силы Х₁ от этой силы, равной единице; 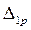– перемещение по линии действия силы Х₁ от внешней нагрузки.

Для определения коэффициентов используем правило Верещагина. Если эпюры изгибающих моментов М_р или содержат несколько участков, то правило Верещагина должно быть использовано для каждого из участков по отдельности.

Поэтому в общем случае искомое перемещение, например 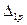, определяется по формуле

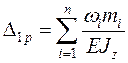, (1.12),

где n – количество участков, на которые разбиваются эпюры изгибающих моментов ; _i – площадь грузовой эпюры, т.е. эпюры М_р на i -мучастке; – ордината эпюры на i- мучастке, расположенная под центром тяжести эпюры M_pi; EJ –жесткость стержня.

5. Определяем коэффициент .

Для этого предварительно строим в о.с. эпюру изгибающего момента 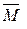от действия силы (рис. 1.10,г.). Далее, используя формулу (1.8), «умножаем» эпюру саму на себя. Получим

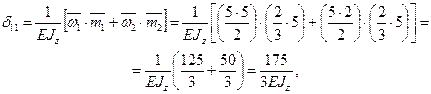
где 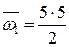– площадь первого участка эпюры 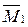; 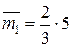– ордината центра тяжести площади первого участка эпюры 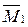; 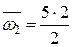– площадь второго участка эпюры 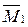; 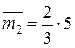– ордината центра тяжести площади второго участка эпюры .

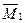6. Определяем коэффициент .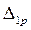

Для определения коэффициента 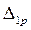необходимо построить эпюру изгибающего момента М_р от действия внешней нагрузки, приведенной на рис. 1.10,в. Для упрощения процесса перемножения эпюр будем строить эпюры внутренних изгибающих моментов от каждой внешней нагрузки отдельно, используя принцип независимости действия сил (принцип суперпозиции). Результат построения показан на рис. 1.10,д. При этом нет необходимости предварительно определять реакции опор. Достаточно на консоли АВ построить эпюру изгибающего момента от распределенной нагрузки q (M_pq) (это вогнутая парабола с высотой 250 кНм) и соединить ординату эпюры M_pq на опоре В с ординатой эпюры M_pq на опоре С, равной 0. Аналогично определив ординаты эпюры M_pМ на опоре В и на опоре С, соединяем их прямой линией. Очевидно, что . При этом также очевидно, что для получения результата необходимо перемножить эпюру M_pq с эпюрой на двух участках, а эпюру M_pМ с эпюрой M – на одном.

Далее, используя формулу (1.12), «перемножаем» эпюры М_р и . При этом на первом участке нужно «умножить» вогнутую параболу на треугольник, на втором – эпюру, состоящую из треугольника – на треугольник, а на третьем – эпюру, состоящую из треугольника – также на треугольник, но с вершинами, не лежащими на одной вертикали.

7. Вычисляем значение лишней неизвестной

.

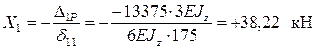Так как , статическая неопределимость балки раскрыта. Далее решение строится обычным образом для расчета балки на изгиб.

8. Загружаем о.с. внешней нагрузкой и силой Х₁ (рис. 1.11,а).

9. Строим эпюру внутренней поперечной силы Q_у и внутреннего изгибающего момента М_z. (рис. 1.11,б и рис. 1.11,в). Предварительно необходимо определить реакции опор B и С.

.

.

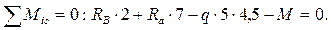
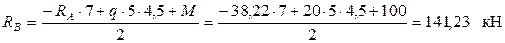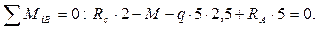
Знак минус означает, что реакция R_C направлена в сторону, противоположную предварительно выбранной и направленной вверх. Зачеркиваем R_C и показываем истинное направление реакции опоры.

Проверка:

; .

На балке два участка. Составляем уравнения для Q и М на участках:

Участок I: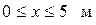

На участке особенная точка Определяем ее координаты и находим максимальный момент на участке I.

Из анализа эпюры M_z следует, что максимальный по модулю изгибающий момент действует в сечении по опоре С: .

10. Подбираем поперечное сечение балки в виде двутавра из условия прочности по нормальным напряжениям

, .

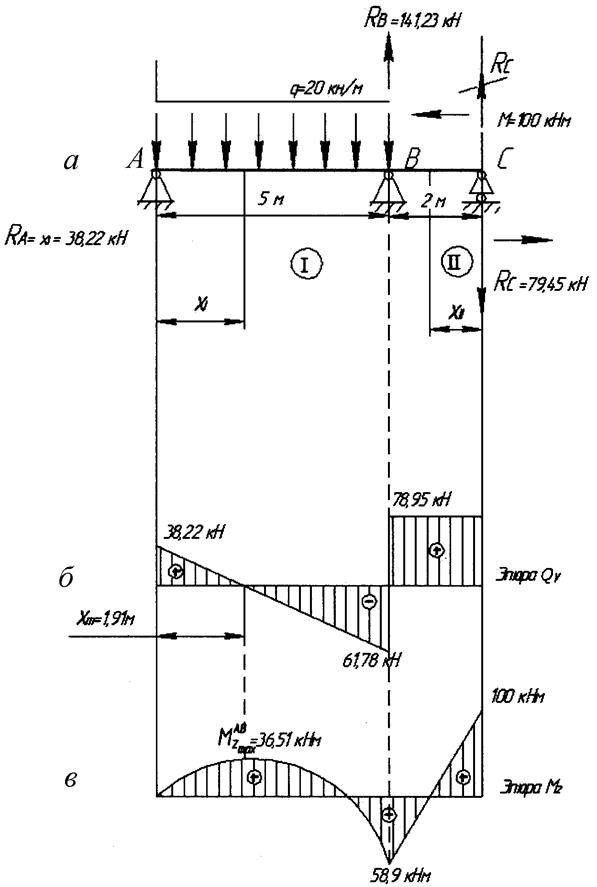
Рис. 1.11.

Из сортамента (Прил. 2) выбираем двутавр I №33, у которого момент сопротивления . Действующие максимальные напряжения:

.

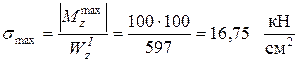Максимальные действующие напряжения меньше допускаемых. Прочность обеспечена.

Примечание: стандартом допускается превышение максимальных действующих напряжений над допускаемыми, но не более чем на 5%.

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: