Основные теоретические сведения

 

1. Расчет вала на изгиб и кручение

Изгиб с кручением круглого вала – вид деформирования стержней, который часто встречается в машиностроении. По этой схеме работает подавляющее большинство валов машин: паровых и газовых турбин, двигателей внутреннего сгорания, редукторов, электродвигателей и прочих. На рис. 2.1,а приведена схема нагружения стержня, а на рис. 2.1,б – эпюры изгибающих и крутящего моментов. Изгибающий момент в опасном сечении:

, (2.1)

где , .

Поскольку при изгибе круглого стержня косой изгиб невозможен, можно найти изгибающий момент проще – . Однако такой подход пригоден для простой расчетной схемы на рис. 2.1,а. При расчете валов машин в разных сечениях вала нагрузки действуют по разным направлениям. Поэтому приходится раскладывать силы на вертикальную и горизонтальную оси, строить эпюры изгибающих моментов, действующих в вертикальной и горизонтальной плоскостях, и находить изгибающий момент геометрическим суммированием по формуле (2.1).

a б

Рис. 2.1.

 

 

В опасном сечении стержня (у заделки) от изгиба возникают нормальные напряжения, от кручения – касательные. Из графиков их распределения (рис. 2.2,а) видно, что максимальных значений они достигают в одной точке – точке С (или точке D) – крайних точках сечения. В этой точке имеет место плоское напряженное состояние (рис. 2.2,б).

a б

Рис. 2.2.

 

В опасной точке С опасного сечения:

(2.2)

. (2.3)

Проверку прочности необходимо делать по III-й или по IV-й теориям прочности. Напряженное состояние в точке С идентично напряженному состоянию при поперечном изгибе, поэтому используем следующие формулы:

(2.4)

. (2.5)

Если в условия прочности подставить формулы нормальных и касательных напряжений в опасном сечении, учтя при этом, что , получим следующее выражение для условий прочности круглого стержня при изгибе с кручением:

(2.6)

. (2.7)

Эти выражения удобно представить в форме, аналогичной условию прочности по нормальному напряжению при изгибе:

(2.8)

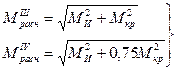. (2.9)

2. Расчет на прочность при повторно переменной нагрузке

Известны многие попытки создания гипотез усталостного разрушения в сложном напряженном состоянии. Все они сводятся к обобщению известных гипотез прочности и пластичности на случай цикличных напряжений. Для наиболее часто встречающегося на практике случая изгиба с кручением общепринятой является эмпирическая формула:

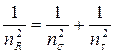, (2.10)

где 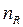– коэффициент запаса усталостной прочности, 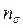– коэффициент запаса по нормальным напряжениям, в предположении, что , – коэффициент запаса по касательным напряжениям, в предположении, что .

Эту формулу легко преобразовать в условие усталостной прочности:

. (2.11)

Условие статической прочности может быть записано в соответствии с III-й теорией прочности в виде:

. (2.12)

Ориентировочные значения величин допускаемого значения коэффициента запаса прочности приведены в табл. 2.1.

Таблица 2.1

Факторы, влияющие на запас прочности. Для расчета на статическую прочность по пределу текучести
Весьма пластичный материал	1,2…1,5
Пластичный материал	1,4…1,8
Малопластичный материал	1,7…2,2
Хрупкий материал	2,0…3,0

Окончание таблицы 2.1

Факторы, влияющие на запас прочности. Для расчета по пределу выносливости при циклической нагрузке
При повышенной точности расчета, однородном материале, широком использовании экспериментальных данных, высоком качестве технологии	1,3…1,5
При недостаточном объеме экспериментальных данных о нагрузках и характеристиках прочности, при ограниченном числе натуральных усталостных испытаний, среднем уровне однородности материала, технологии производства и дефектоскопии	1,5…2,0
При малом объеме и отсутствии экспериментальной информации о нагрузках и прочности, при невысоком уровне технологии производства, пониженной однородности материала (литые и сварные детали значительных размеров)	2,0…3,0

 

 

З а д а н и е

 

Вал, лежащий на двух опорах, загружен произвольной системой сил: P_1,Р₂, Т₁ Т₂, А, (рис. 2.3, табл. 2.2). Подобрать поперечное сечение вала из условий прочности и жесткости, если вал принимает мощность N с угловой скоростью ω. В расчете использовать третью теорию прочности, полагая допускаемые напряжения равными . Прогиб вала не должен превышать 1/400 пролета. Рассчитать вал на циклическую прочность, считая, что вращающийся вал испытывает переменный изгиб с коэффициентом асимметрии . Одновременно вал подвергается кручению с коэффициентом асимметрии . Материал вала Ст45. 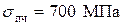Модуль Юнга , предел прочности , предел текучести , пределы выносливости , . Поверхность вала шлифованная, коэффициент, учитывающий влияние обработки поверхности, равен . Коэффициент, учитывающий масштабный эффект, равен .

В опасном сечении вала имеется отверстие для смазки диаметром , для которого теоретические коэффициенты концентрации напряжений составляют: при изгибе , при кручении . Для расчета принять трубчатое сечение вала с наружным диаметром D, внутренним диаметром . Расчетные схемы и исходные данные представлены на рис. 2.3 и в табл. 2.2.

 

 

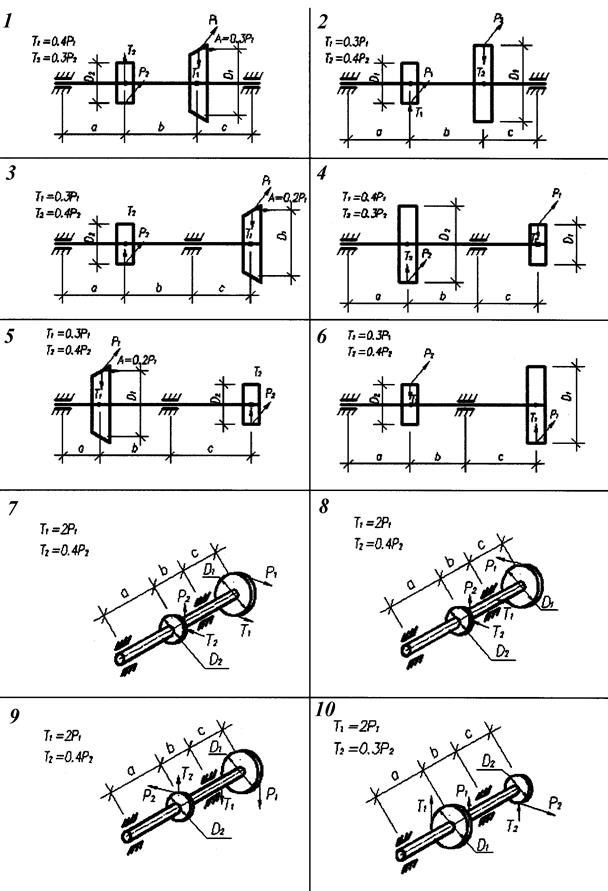
Рис. 2.3.

Таблица 2.2

№ строки	№ схемы	Мощность N	Угловая скорость ω	а	в	с
		кВт	с-1	м	мм	мм
				0,2	0,4	0,3
				0,2	0,8	0,35
				0,2	0,80	0,50
				0,30	0,40	0,40
				0,80	0,60	0,40
				0,40	0,40	0,50
				0,40	0,70	0,20
				0,30	0,60	0,50
				0,60	0,30	0,20
				0,40	0,50	0,60

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: