 |
Определение диаметра вала из условия жесткости
|
|
|
|
Определим прогиб вала в вертикальной плоскости по формуле (1.1). Расчет прогиба произведем методом начальных параметров. Угол поворота на опоре А найдем из условия отсутствия прогиба на правой опоре.
При х =0,9 м 
.
,
,
.
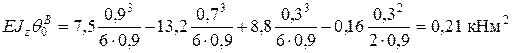Прогиб при x =0,2 м
,
.
Прогиб при х = 0,6 м
;
.
Аналогично определим горизонтальный прогиб вала.
Угол поворота на левой опоре А 
найдем из условия отсутствия прогиба на правой опоре.
При х = 0,9 м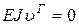 
.
,
,
.
Прогиб при х = 0,2 м
;
.
Прогиб при х = 0,6 м в горизонтальной плоскости
;
.
Суммарный максимальный прогиб будет в точке с координатой х = 0,2 м
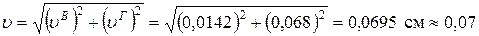см.
Допускаемый прогиб 
, равен 1/400 пролета L = 90 cм, т.е.
.
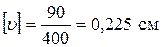Прогиб, который будет иметь место, при принятом диаметре вала 70 мм, получили равным 0,07 см, т.е. 
.
Жесткость обеспечена.
Окончательно принимаем D = 70 мм.
В случаях, если оказывается что 
, назначают диаметр вала исходя из значения осевого момента инерции, который определяют из неравенства:
; 
,
где 
– фактический максимальный прогиб; – допускаемый прогиб; 
– момент инерции, полученный из условия расчета на прочность; 
– минимально допустимый осевой момент инерции, из условия расчета на жесткость.
Диаметр 
определяют из условия 
.
В дальнейшем в расчет принимают значение диаметра вала, которое одновременно удовлетворяет условиям прочности и жесткости.
Пример расчета на прочность при повторно-переменной нагрузке
Решение
Моменты сопротивления принятого сечения:
,
.
Максимальные амплитудные напряжения при изгибе:
.
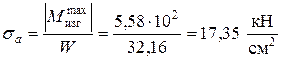Максимальный изгибающий момент при 
кН·м.
Минимальные нормальные напряжения:
.
Максимальные касательные напряжения при кручении:
.
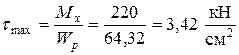Минимальные касательные напряжения:
|
|
|
.
Средние касательные напряжения:
.
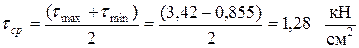Амплитудные напряжения:
.
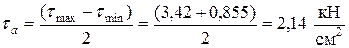Эффективный коэффициент концентрации по нормальным напряжениям
.
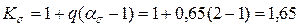Для касательных напряжений:
,
где q – коэффициент чувствительности материала к концентрации напряжений, для принятой стали равен 0,65; 
– теоретические коэффициенты концентрации напряжений (даны в условии задачи).
Общий поправочный коэффициент для нормальных напряжений:
.
Для касательных напряжений:
.
Коэффициент запаса при изгибе вала (симметричный цикл – средние нормальные напряжения равны нулю)
.
Здесь ψ – коэффициент приведения асимметричного цикла к равноопасному симметричному, определяется по формуле
,
где σв – предел прочности, в МПа. При кручении 
, 
, для симметричного цикла.
Коэффициент запаса при кручении:
,
здесь 
.
При кручении 
.
Общий коэффициент запаса
(принято по табл. 2.1)..
Таким образом, вал диаметром 70 мм не удовлетворяет условию циклической прочности. Изменим для его исполнения марку стали. Примем легированную сталь 40 ХНМА (Прил. 3) с характеристиками прочности σпч =1500 МПа, σт = 1000 МПа, σ-1 = 700 МПа, τ-1 = 450 МПа, не изменяя принятые ранее коэффициенты.
Коэффициент запаса при изгибе вала:
Коэффициент запаса при кручении:
Здесь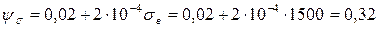 
.
При кручении 
.
Общий коэффициент запаса
Таким образом, вал диаметром 70 мм удовлетворяет требованиям прочности, жесткости и расчету на повторно-переменную (циклическую) нагрузку при использовании легированной стали 40ХНМА.
Расчетно-графическая работа №3
РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ,
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ ПРИ УДАРЕ
Общие указания
Работа состоит из двух основных частей. В первой части, посвященной устойчивости сжатых стержней, необходимо решить две задачи. Сначала по известной нагрузке необходимо подобрать поперечное сечение стержня. Затем для стержня с сечением, составленным из стандартного профиля с известными размерами, предлагается рассчитать его грузоподъемность (допускаемую нагрузку) и определить частоту собственных колебаний. Во второй части, посвященной разделу «Динамика», необходимо определить напряжения, возникающие в стержне от действия ударной нагрузки. Краткие теоретические сведения приведены в параграфах, предшествующих рассмотрению каждой из частей.
|
|
|
|
|
|
