Метод системной динамики Дж. Форрестера

Системная динамика – это метод моделирования и имитации сложных динамических экономических систем, характеризующихся разветвленными и, в общем случае, нелинейными структурами – контурами регулирования.

Основные работы Дж. Форрестера (Основы кибернетики предприятия (индустриальная динамика). - М.: Прогресс, 1971; Динамика развития города. - М.: Прогресс, 1974; Мировая динамика. - М.: Наука, 1978) посвящены анализу промышленных предприятий, развития городов и региональных систем. В моделях Дж. Форрестера анализируются в различных политических и экономических аспектах следующие важнейшие факторы, имеющие глобальное значение: население, сельскохозяйственное производство, природные ресурсы, промышленное производство, загрязнение окружающей среды. В основе моделей Форрестера лежат общие структурные элементы, пригодные для моделирования практически любых экономических систем:

1. темпы – параметры потоков, исходящих от одних интегрирующих звеньев и поступающих в другие и вызывающих в обеих группах соответствующие изменения;

2. уровни – регулируемые объекты, формально отображающие переменные, фигурирующие в системе, параметры которых получены интегрированием соответствующих характеристик потоков;

3. функции решений – соотношения, отражающие функциональные зависимости, существующие в системе, они определяют интенсивности входящих и исходящих потоков; это регуляторы многоконтурной системы регулирования;

4. вспомогательные величины, активно участвующие в определении общих характеристик;

5. параметры – константы модели.

Системная динамика представляет собой совокупность принципов и методов анализа динамических управляемых систем с обратной связью и их применения для решения производственных, организационных и социально-экономических задач. В системах поддержки принятия решений применение системной динамики позволяет объединить несколько функциональных пространств организации в одно целое и обеспечить организационный и количественный базис для выработки более эффективной управленческой политики. Три достижения, обеспеченные в основном благодаря разработкам в области вооружений, сделали возможным применение системной динамики:

1. Успехи в проектировании и анализе систем управления с обратной связью.

2. Прогресс в методах компьютерного моделирования и развитие вычислительной техники.

3. Накопленный опыт в моделировании процесса принятия решений.

На первое место по своей важности следует поставить осознание необходимости развития динамических информационных систем с обратной связью, которые появились уже после того, как подобные электромеханические, а затем и электронные системы стали широко применяться на практике. Другим основным достижением, которое легло в основу системной динамики, является компьютерное моделирование. Уже много лет моделирование – важнейшая составная часть инженерного проектирования. Применение методов имитационного моделирования в технике, предшествующее созданию опытных образцов, обусловило их распространение на проблемы планирования и управления в организационных системах. С появлением надежных и высокопроизводительных персональных компьютеров моделирование сложных организаций стало практической задачей. Ограничения на размерность и вид математических моделей сейчас практически сняты.

Наконец, наряду с этими достижениями, пришло более глубокое понимание того, как организован процесс принятия решений человеком. Расширение наших знаний в этой области было вызвано потребностями военных исследований для автоматического и автоматизированного управления оружием. Успех в этой области убедил в том, что человеческое мышление и действия доступны не только тщательному изучению, пониманию и произведению, но даже и улучшению.

Философия системной динамики базируется на предположении, что поведение (или история развития во времени) организации главным образом определяется ее информационно-логической структурой. Она отражает не только физические и технологические аспекты производственных процессов, но, что гораздо важнее, политику и традиции, которые явно или неявно определяют процесс принятия решений в организации. Такая структурная схема содержит источники усиления, временных задержек и информационных обратных связей, подобных тем, которые встречаются в сложных инженерных системах. Инженерные и управляющие системы, содержащие подобные элементы, генерируют сложные ответные реакции даже на относительно простые изменения системы или входного сигнала. Анализ больших нелинейных систем такого рода представляет трудную задачу даже для опытных инженеров-системотехников, не говоря уже о быстром и надежном перепроектировании (реинжениринге) таких систем. Тонкости и специфика, присущие области управления, делают эти проблемы еще более сложными. В этом случае структурная ориентация системной динамики представляет собой первый шаг в процессе замены хаоса порядком.

Математическим аппаратом системной динамики являются обыкновенные дифференциальные уравнения первого порядка, причем, по мнению Дж. Форрестера, "все системы, изменяющиеся во времени, могут быть представлены в виде взаимодействия только темпов и уровней, которые полностью описывают состояние системы в любой момент времени, то есть эти два типа переменных не только необходимы, но и достаточны для описания любой динамической системы". Изначально построение и анализ системно-динамических моделей носили больше алгоритмический, нежели аналитический характер, то есть были ориентированны на использование вычислительных средств для решения алгоритмических, а не аналитических задач. А благодаря созданию объектно-ориентированных языков программирования ("DYNAMO", "STELLA", "VENSIM", "POWERSIM" и другие) стало возможным создавать довольно большие модели, включающие тысячи переменных, которые могли описывать динамику сложных систем.

В результате развития данного направления системного анализа были сформулированы специфические принципы и правила построения, использования и интерпретации системно-динамических моделей.

Основными принципами системной динамики являются следующие утверждения:

1) поведение системы - это следствие проявления ее структуры и взаимодействия ее элементов;

2) структура системы и характер взаимосвязей между элементами системы, определяющие ее поведение, более важны, нежели количественные оценки для понимания поведения системы;

3) состояние системы и ее структура есть причина изменений, а не их результат;

4) проблемы возникают внутри системы, а не вне ее;

5) изучить систему - значит определить ее состав и установить отношения между ее элементами, то есть ее структуру;

6) определяющее значение в поведении системы имеет взаимодействие контуров обратной связи в ее структуре;

7) в контурах обратной связи и консервативных подсистемах всегда присутствуют уровни и темпы;

8) уровни и темпы являются необходимыми и достаточными переменными для описания любой динамической системы;

9) при построении системно-динамических моделей следует опираться на принцип "непосредственной верификации"⁶⁴ или валидности (обоснованности);

10) при изучении системы важно концентрировать внимание на анализе действенности политик (управленческий аспект), а не на точном получении количественных оценок.

Из этих принципов следует, что при построении модели, основное внимание уделяется отысканию структуры системы, которая воспроизводила бы динамику протекающих в ней процессов. При этом, в качестве строительных "кирпичиков" используются контуры обратной связи (положительной и отрицательной). Важно отметить, что при этом параметры, характеризующие данные контуры обратной связи могут задаваться с большими погрешностями без существенного влияния на результаты моделирования. Именно это свойство системно-динамических моделей позволяет моделировать сложные системы при наличии неполноты информации. Однако не следует думать, что системно-динамические модели изначально неточны в определении количественных характеристик. Они становятся точными для хорошо структуризованных систем и процессов.

Идентификация системно-динамических моделей заключается в следующем:

• модель должна выходить на все равновесные траектории, присущие системе;

• модель должна адекватно, но необязательно точно, отражать время перехода между равновесными (квазистационарными) состояниями;

• модель должна передавать динамику процессов, протекающих в системе как в состояниях равновесия (то есть описывать установившиеся процессы, включающие в себя колебательный режим или стабильное равновесие), так и в переходный период (переходные процессы). Причем, если в системе существует колебательный режим, то модель должна адекватно передавать амплитуду и частоту колебаний. При этом достаточна лишь точная передача характера поведения системы, а не точное вычисление значений переменных системы, хотя последнее возможно в условиях полноты информации.

Отсюда следует, что из системно-динамических моделей, прежде всего, извлекается поведенческая информация, описывающая траектории развития системы в целом. То есть на базе системно-динамических моделей можно отслеживать характер фазовых переходов системы из одного квазиравновесного состояния в другое, а также поведение системы в равновесных состояниях. Кроме того, современные средства разработки анализа системно-динамических моделей (например, VENSIM, POWERSIM, STELLA и другие) позволяют осуществлять этот процесс быстро и эффективно для систем практически любого масштаба и уровня сложности, а результаты анализа наглядно представлять в виде различных диаграмм, таблиц и так далее. Одновременно с этим они позволяют находить оптимальные стратегии, то есть линии поведения для лиц, принимающих решения, на основе аппарата многокритериальных оценок, а также посредством применения оптимизирующих алгоритмов, то есть нахождения максимума или минимума соответствующего целевого функционала.

Таким образом, мы видим, что в настоящее время системно-динамический подход, позволяет не только сочетать в себе практически большинство современных методов системного анализа, но и служить удобным инструментом изучения сложных систем в различных сферах. Прежде всего, это достигается наглядностью в описании сложных систем на диаграммном языке, который позволяет, используя инструментарий объектно-ориентированного программирования, быстро создавать и анализировать структурную схему исследуемой системы, владея минимальными знаниями в области высшей математики и программирования. Этот же диаграммный язык (диаграммная техника) позволяет так же обсуждать полученную системно-динамическую модель и результаты имитационных экспериментов со специалистами из разных областей, что является несомненным преимуществом для изучения социо-эколого-экономических систем. А это, в свою очередь, требует междисциплинарного подхода.

Кроме того, специалисты, владеющие различными математическими методами и программированием, могут при помощи современных достижений в области системной динамики делать следующее:

1) анализировать эффективность тех или иных математических методов, заложенных в модель (например, точности вычисления по методу Эйлера или Рунге-Кута 4-го порядка, применение методов Монте-Карло или Латинского Гиперкуба при проведении имитационных экспериментов);

2) расширять при помощи создания макросов, DLL-библиотек и графического интерфейса и подстраивать под свои нужды визуальные средства разработки имитационных моделей, такие как VENSIM, POWERSIM.

3) создавать на базе разработанных моделей деловые игры с удобным для пользователя интерфейсом;

4) создавать при помощи POWERSIM мультиплатформенные сетевые обучающие системы и имитационные модели с использованием современных сетевых информационных технологий без непосредственного изучения специализированных средств разработки таких, как язык программирования JAVA;

5) разрабатывать при помощи визуальных языков программирования (Visual Basic, C++, Delphi и других) экспертные системы или другие приложения с использованием полученных моделей в качестве DLL-библиотек (VENSIM, POWERSIM);

После освещения концепции системной динамики ее возможностей перейдем к описанию основных понятий и инструментария системно-динамического подхода.

Рассмотрим основные понятия системной динамики, которые представляют собой основу имитационного моделирования. При этом будем опираться на кибернетическую трактовку понятия системы, а именно, под системой будем понимать множество взаимосвязанных элементов вместе с отношениями между элементами и их атрибутами. Причем под элементом системы понимается неразложимый компонент сложных объектов, явлений, процессов, т. е. неделимая часть системы. При этом можно выделить следующие четыре признака системы:

1) целостность системы, то есть принципиальную несводимость свойств системы к сумме свойств составляющих ее элементов и ее относительную независимость от других аналогичных систем;

2) наличие цели у системы и критерия исследования множества ее элементов;

3) наличие внешней среды, то есть более крупной и внешней по отношению к данной системы;

4) возможность выделения подсистем, то есть взаимосвязанных частей в данной системе, представляющих собой системы по отдельности.

Важно отметить, что вышеупомянутая неразложимость элементов системы понимается в рамках заданного способа рассмотрения и анализа системы, то есть критерия ее исследования. Возможность выделения подсистем приводит к построению структуры системы, под которой понимается совокупность и характер отношений между элементами (подсистемами) системы и их атрибутами. При этом совокупность элементов системы образует ее состав, а каждый элемент системы можно рассматривать как "черный ящик" (до определенного момента времени). Совокупность же состава и структуры системы образует структурную схему системы.

При рассмотрении сложных систем, которые характеризуются наличием дублирующих элементов и обратных связей, важно учитывать такое их свойство, как эмерджентность, то есть наличие у системы свойств, которые не присущи ни одному из составляющих ее элементов, взятому в отдельности. Эмерджентность системы отражает ее целостность и является результатом возникновения между элементами системы так называемых синергетических связей. Они обеспечивают неравенство общего эффекта от взаимодействия всех элементов системы и суммарного эффекта от взаимодействия отдельных элементов системы между собой, как если бы их можно было рассматривать независимо друг от друга. Эмерджентность, как правило, и приводит к обнаруженному Дж. Форрестером "контринтуитивному поведению" сложных систем, о котором упоминалось во введении.

После определения состава системы необходимо выявить структуру системы. Обычно она задается исходя из ментальной модели изучаемой системы. При этом устанавливаются взаимосвязи между элементами системы, характеризуемых при помощи различных атрибутов (материальных, финансовых, информационных). Для этого зависимые элементы соединяют стрелкой, начинающейся у влияющего элемента и заканчивающейся у того элемента, на который предыдущий (влияющий) элемент оказывает воздействие.

При этом мы получим причинно-следственную диаграмму. В литературе так же можно встретить синонимичные термины, обозначающие причинно-следственные диаграммы, такие как "диаграммы влияний", "когнитивные карты" и другие. Для отражения характера связи между указанными элементами введем такие понятия, как положительное (отрицательное) воздействие переменной А на переменную Б, которые сопоставляются с данными элементами. Обе переменные зависят от времени. Согласно классическому определению, широко распространенному в отечественной и зарубежной литературе, переменная А оказывает положительное (отрицательное) воздействие на переменную Б, если при прочих равных условиях изменение переменной А ведет к изменению переменной Б в том же (в противоположном) направлении. При этом рядом со стрелкой, связывающей элементы А и Б ставится знак "+" в случае положительного воздействия А на Б или знак "-" в случае отрицательного воздействия.

Это определение оказывается некорректным, когда в качестве переменной А выбирается переменная, имеющая характер скорости (темповая переменная), а в качестве переменной Б выбирается переменная, обладающая кумулятивным свойством (переменная уровня). Например, рождаемость и численность населения. Так, при увеличении рождаемости численность населения возрастает. Однако, с уменьшением рождаемости численность населения не уменьшается, а продолжает увеличиваться, но более медленно. Это противоречие было впервые обнаружено Дж. Ричардсоном в 1976 году.

Таким образом, классическое определение верно работает только при установлении связи между переменными одного типа, и в противоположном случае (связь между разнотипными переменными) только при условии положительного изменения величины А. В общем случае, при рассмотрении связи между разнотипными переменными на причинно-следственной диаграмме, корректно использовать свободное от указанных недостатков следующее определение положительного (отрицательного) воздействия элемента А на элемент Б:

переменная А оказывает положительное (отрицательное) воздействие на переменную Б, если при прочих равных условиях увеличение переменной А ведет к увеличению (уменьшению) переменной Б.

Для определения контуров обратной связи удобно использовать язык орграфов (ориентированных графов), однако мы ограничимся неформальными определениями. Обычно вводится понятие замкнутой цепи (цикл в неориентированном графе) или замкнутого пути (контур в ориентированном графе), по которому можно от любого одного элемента, входящего в контур, добраться до любого другого элемента, путешествуя только по данной цепочке или пути. Обычно такой контур называют контуром обратной связи, а связь между выходными параметрами системы (концом пути) и входными параметрами системы (началом пути) обратной связью. Для иллюстрации рассмотрим процедуру начисления сложных процентов, изображенную на следующей структурной схеме (рис. __):

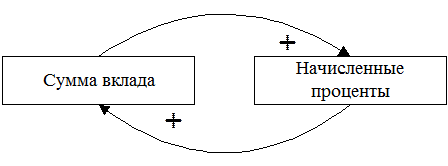
Рис.___ Схема начисление сложных процентов

 

Согласно классическому определению, положительный контур обратной связи часто определяется так, что "начальное изменение любой переменной (в контуре), в конечном счете, стимулирует далее самоизменение в первоначальном направлении". При этом контур положительной обратной связи часто называют "порочным кругом", примером которого может служить инфляционная спираль "зарплата-цены". Таким образом, положительная обратная связь приводит к разбалансировке системы и даже к ее разрушению, вызывая изменения по типу цепной реакции.

Для отрицательного контура обратной связи имеем следующее классическое определение: "Если отклик контура обратной связи на переменное изменение выступает против первоначального возмущения, то контур является отрицательным или целенаправленным". Определение отрицательного контура обычно интерпретируется таким образом, что "изменение одного элемента (контура обратной связи) распространяется по кругу, пока не вернется, чтобы изменить тот же элемент в направлении, противоположном начальному изменению". Отрицательную обратную связь часто называют "благожелательной", поскольку она не позволяет системе разрушиться в результате внешних воздействий.

После анализа основополагающей терминологии системной динамики, рассмотрим классификацию и обозначения элементов модели (для языка VENSIM)

1) Переменные уровней (Level) - обладают кумулятивным, то есть накопительным свойством (резервуары). Полностью описывают состояние системы и изменяются только за счет переменных темпов. Определяются при интегрировании уравнений уровней (обыкновенных дифференциальных уравнений первого порядка) с заданными начальными условиями в промежутке между моментом времени tj и t_K, где индексы J.K нумеруют соответственно прошедший и настоящий моменты времени. Количество переменных уровня определяют порядок системы.

2) Переменные темпов (Rate) - играют роль скоростей и характеризуют потоки, входящие и выходящие из резервуаров. Зависят только от переменных уровней, констант и вспомогательных переменных. Не зависят непосредственно друг от друга. Описывают вместе с переменными уровня сохраняющиеся потоки. Являются источником изменений динамики системы в результате принимаемых управленческих решений.

3) Вспомогательные переменные (Auxiliary) - необходимы для определения переменных темпов и вводятся для более простого представления системы. Участвуют при формировании вспомогательных уравнений, необходимых для решения уравнений темпов.

4) Константы (Constant) - относятся к экзогенным переменным системы и необходимы для определения экзогенных параметров модели. Изображаются в виде надписей без обрамлений.

5) Табличные функции (Lookup) - используются для связи между переменными, устанавливаемой не аналитически, а при помощи экспертных оценок. Как правило, табличные функции используются для косвенной связи эндогенных переменных модели, и изображаются при помощи названия без обрамления, в которое обязательно входит слово функция. Однако иногда они могут быть использованы для задания динамических рядов, описывающих экзогенные параметры модели.

Кроме вышеупомянутых переменных в современных языках системно-динамического моделирования, таких как VENSIM и POWERSIM есть два дополнительных типа переменных, которые никак не связаны со структурой рассматриваемой модели, но которые помогают проверять динамические гипотезы, калибровать и улучшать модель или ее компоненты (на основе поведенческой матрицы, описанной в следующем параграфе). Эти переменные не относятся к вышеупомянутым дополнительным переменным.

Первый тип переменных представляет собой переменные "тестовых вводов" (TEST INPUTS) или просто "тестовые" переменные, значениям которых присваиваются временные ряды, константы или альтернативные уравнения, соответствующие динамическим гипотезам вида "при таких-то условиях, система должна вести себя так-то". По сути, этот тип переменных представляет собой табличные функции константы и уравнения, отражающие реальное поведение системы в различных режимах. Однако в альтернативные уравнения могут входить алгебраические и одновременные выражения и не могут входить определенные функции, такие как интегрирование (INTEG) и некоторые другие.

Указанные переменные используются только в переменных второго типа, называемых "ограничениями" (CONSTRAINTS), которые представляют собой логические условные процедуры, нарушение которых фиксируется во время имитации, но не приводит к ее остановке. При этом, если условие "ограничения" нарушается для какой либо величины, то в местах несоответствия моделируемого поведения реальному в модель могут подставляться результаты реального поведения системы. Кроме того, использование данных переменных может приводить к реструктуризации модели (по желанию исследователя) во время проведения ее тестирования на предмет соответствия реальному поведению системы. Однако после проведения таких проверок происходит возврат к исходной структуре.

Теперь, после описания основных понятий системной динамики, перейдем к рассмотрению процедуры построения имитационных моделей.

Построение имитационных моделей не является четко формализованной процедурой, поскольку, прежде всего, это творческий процесс. Однако выделение основных этапов имитационного моделирования помогает не только логически упорядочить последовательность выполняемых действий, но и свести к минимуму ошибки и лишние операции при построении и использования имитационных моделей. Кратко построение имитационных моделей можно разбить на следующие этапы:

1) формулировка целей исследования и постановка проблем, которые необходимо решить для достижения поставленных целей;

2) сбор и обработка информации о моделируемой системе и протекающих в ней процессах (этап "референции"):

- фильтрация (отбор) информации,

- распределение информации согласно картинам поведения системы (составление матрицы картин поведения системы);

3) построение концептуальной модели:

- определение структуры и границ системы (сочетается с составлением матрицы картин поведения системы),

- определение основных и вспомогательных переменных, выдвижение "динамических гипотез",

- построение диаграммы причинно-следственных связей,

- построение диаграммы потоков (материальных, финансовых, информационных),

- уточнение количественных соотношений между переменными модели (использование статистических программных пакетов, методов экспертных оценок),

- написание основных и вспомогательных уравнений;

4) построение машинной (компьютерной) модели с использованием одного из визуальных средств (языков) имитационного моделирования (STELLA, DYNAMO, VENSIM, ИМИТАК, GPSS и так далее):

- ввод концептуальной модели,

- построение графического интерфейса (диаграмм, графиков, элементов управления);

5) проведение имитационных экспериментов и верификация модели:

- проверка динамических гипотез и сравнение поведения модели с данными, собранными на этапе "референции",

- проверка имитационной модели на устойчивость по отношению к вариации начальных условий и изменению структуры модели,

- обработка результатов имитационных экспериментов;

6) обсуждение (дебрифинг) модели с экспертами, общественностью, заказчиком;

7) улучшение модели;

8) применение модели для решения практических задач и в учебном процессе.

Перечисленная выше последовательность этапов допускает возвращение от последующего этапа к предыдущим для внесения уточнений в разрабатываемую имитационную модель. Данная последовательность этапов не является единственно возможной. Более свернутую последовательность этапов построения имитационных моделей можно встретить в работах. Так, первые два этапа некоторые авторы совмещают с третьим, а построение диаграмм потоков и следующие за ним подэтапы третьего этапа включают в четвертый этап. Однако по своей сути все существующие в настоящее время схемы, описывающие последовательность действий по разработке и применению имитационных моделей, эквивалентны. Важной деталью, объединяющей все такие схемы, является наличие обратных связей между этапами имитационного моделирования. Например, Дж. Форрестер, приводит следующую схему имитационного моделирования, иллюстрирующую наличие обратных связей между различными этапами моделирования (рис. __):

Рис. ___ Схема процедуры построения системно-динамической модели по Дж. Форрестеру

 

Далее рассмотрим более подробно каждый из девяти этапов указанной ранее схемы.

Формирование целей исследования представляет собой первоначальный этап изучения системы и протекающих в ней процессов, который во многом определяет направления дальнейшего исследования. Вместе с формулировкой целей исследования формулируются те проблемы, которые должны быть решены при помощи имитационного моделирования для достижения поставленных целей. Правильная формулировка целей и проблем – половина успеха. Однако в ходе исследования цели и проблемы могут изменяться, поскольку построение имитационной модели может вскрыть первоначально невидимые свойства и поведение системы и тем самым либо скорректировать сформулированные ранее цели исследования и поставленные проблемы, либо добавить к ним новые. Обычно исследование проводится для достижения следующих целей:

- упорядочивание знаний и улучшение нашего понимания поведения исследуемой системы и протекающих в ней процессов;

- поиск стратегий, способных изменить поведение системы в желаемом направлении;

- отражение ментальных моделей для их унификации и обмена знаниями о поведении системы между широкими слоями населения.

Установив цели исследования, переходим к следующему этапу моделирования.

Сбор и обработка информации о моделируемой системе и протекающих в ней процессах ("этап референции") является неотъемлемой частью предыдущего и последующих этапов, поскольку собирать и обрабатывать информацию приходится на всех этапах имитационного моделирования. Однако оказывается полезным выделение данного этапа в качестве самостоятельного "этапа референции" в связи с тем, что на данном этапе для более полного описания исследуемой системы накапливается эмпирический материал о поведении изучаемой системы и сходных с ней систем-аналогов. Затем этот материал подвергается фильтрации (например, выбирается одна из повторяющихся картин поведения) и декомпозиции (например, сезонное и циклическое поведение отделяется от тренда).

Построение концептуальной модели представляет собой наиболее трудоемкий и в тоже время наиболее творческий процесс, поскольку необходимо не только четко обрисовать контуры изучаемой системы, но и передать структуру системы таким образом, чтобы, с одной стороны, полученная модель не стала слишком сложной и недоступной для понимания и проведения имитационных экспериментов, а с другой стороны, чтобы полученная модель не стала слишком упрощенной, так как в этом случае она не будет воспроизводить динамику изучаемой системы. Поэтому разумно придерживаться минимальной структуры модели, которая бы воспроизводила указанные в вышеописанной матрице элементы картин поведения реальной системы (класса систем) без существенных искажений. Иначе говоря, минимальная структура должна воспроизводить основные тренды, связанные с протекающими в моделируемой системе процессами, равновесные состояния системы и переходы из одного равновесного состояния в другое. Для этого необходимо пройти несколько этапов:

1. Выделить изучаемую систему из более общей окружающей ее системы на основе данных, полученных на этапе референции. Это осуществляется путем разделения всех элементов, связанных с данной системой, на внутренние (эндогенные элементы, взаимодействующие между собой внутри системы), внешние (экзогенные элементы, воздействующие на систему, но не зависящие от нее) и исключенные (не оказывающие существенного влияния на поведение системы) элементы. Каждый из элементов системы обладает материальным, финансовым и информационным свойствами. Затем необходимо выделить, если это возможно, на основе "поведенческой матрицы" подсистемы в изучаемой системе. Для каждой из выделенных подсистем проделать вышеописанную процедуру.

2. Определить основные и вспомогательные переменные, характеризующие элементы системы. К основным переменным необходимо отнести переменные, характеризующие поведение наиболее важных с точки зрения поставленной задачи элементов системы. К таким переменным, как показывает практика, обычно относят переменные, претендующие на роль потоков и уровней, а к вспомогательным - переменные, характеризующие остальные элементы системы. Причем необходимо для каждой переменной выбрать соответствующую единицу измерения или оставить ее безразмерной. Это поможет не только правильно, с точки зрения размерности записать уравнения, но и представить результаты имитационного моделирования в удобном для анализа и понятном для восприятия виде. Последнее особенно важно для людей, которые в дальнейшем будут использовать построенную имитационную модель либо для принятия управленческих решений, либо в процессе обучения. Далее в терминах основных и вспомогательных переменных необходимо обозначить "динамические гипотезы", характеризующие взаимодействие элементов в изучаемой системе и определяющие ключевые петли обратной связи, лежащие в основе картин поведения, описанных на "этапе референции".

3. Построить диаграммы причинно-следственных связей на основе обозначенных динамических гипотез о взаимодействии элементов системы. Это осуществляется путем связывания при помощи стрелок и знаков"+" и"-" зависимых элементов. В результате получается знаковый орграф, отражающий причинно-следственные связи в системе. Следует отметить, что направление и полярность каждой причинно-следственной связи определяются при фиксации характеристик всех остальных элементов системы. Далее на основе полученного орграфа следует определить контуры положительной и отрицательной обратной связи, а также их вложенность и пересечение (пересечение разнополярных контуров обратной связи может привести к эффекту переключения доминирующего контура обратной связи). Полученный орграф оказывается полезным как для наглядного представления динамических гипотез, так и для представления результатов имитационного моделирования. Однако он несет мало информации о динамике процессов, протекающей в системе, и иногда может приводить к неправильным выводам относительно поведения системы (см. предыдущий параграф). Для устранения этого недостатка необходимо перейти к следующему этапу.

4. Построить диаграммы потоков (материальных, финансовых, информационных). Поскольку каждый элемент системы может участвовать в материальных, финансовых и в информационных потоках, то удобно представлять то или иное свойство (материальное, финансовое или информационное) элемента системы и соответствующие ему потоки на отдельной диаграмме, хотя возможно и пересечение потоков. Сначала следует выбрать элементы причинно-следственной диаграммы, которые могут быть использованы в качестве элементов уровня. К таким элементам можно отнести элементы, которые являются накопителями (резервуарами) тех или иных характеристик системы (материальных, финансовых, информационных) с течением времени. Затем необходимо выделить те элементы, которые будут элементами темпов (скоростей), регулирующих потоки, входящие и выходящие из элементов, выбранных в качестве уровней. Как правило, темпы, регулирующие и входящие и выходящие потоки, зависят от связанных с ними уровней и непосредственно не зависят друг от друга. По определению, в каждой петле обратной связи должна быть хотя бы одна переменная уровня и одна переменная темпа, поскольку в противном случае невозможно будет проследить динамику переменных, входящих в данную петлю обратной связи. Это связано с тем, что все переменные будут заданные в один и тот же момент времени. Отметим, что размерность переменных темпов должна быть равной размерности переменных соответствующих уровней, деленной на размерность времени. Далее необходимо перейти к следующему этапу.

5. Определить начальные условия (задать все необходимые константы), интервалы изменения переменных модели и уточнить количественные соотношения между переменными. При этом предполагается, что основные соотношения между переменными определены интуитивно уже на этапе формулирования "динамических гипотез". Для уточнения этих соотношений необходимо вновь вернуться к информации, которая была накоплена на "этапе референции". Задание численных значений констант в основном необходимо для определения начальных значений уровней, продолжительности и шага моделирования, времен задержек и так далее. Используя статистические программные пакетов для проведения регрессионного и дисперсионного анализа, а также методы экспертных оценок, можно выявить как количественные, так и качественные зависимости между переменными модели. К основным методам регрессионного анализа, используемого при анализе коли