 |
Эконометрический подход к анализу экономических систем
|
|
|
|
Эконометрика как наука расположена где-то между экономикой, статистикой и математикой. Один из ответов на вопрос, что такое эконометрика, может звучать так: это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем данные или «наблюдения» для того, чтобы получить количественные зависимости для экономических соотношений. Данные, как правило, не являются экспериментальными, так как в экономике мы не можем проводить (многократные) эксперименты.
Основным инструментом анализа экономических систем в этом случае является модель. Какой должна быть эконометрическая модель, чтобы можно было считать ее приемлемой для анализа экономических систем. Как сказал Эйнштейн модели должны быть «настолько простыми, насколько возможно, но не проще». В большинстве случаев экономические законы выражаются в относительно простой математической форме.
Применение методов эконометрики к анализу экономических систем требует от исследователей прочных экономических знаний и определенного скептицизма по поводу значимости «теорем» в практических приложениях. Эконометрические модели и методы нашли широкое применение в бизнесе, экономике, общественных науках, анализе экономической активности и даже в исследовании политических процессов. Их полезность обусловлена тем, что они не только показывают как может развиваться тот или иной процесс в экономике, но и раскрывают суть происходящих процессов, снабжая исследователя дополнительной информацией для проведения анализа.
Методологически можно выделить три основных класса моделей, которые при меняются при использовании эконометрического подхода к анализу экономических систем:
|
|
|
1. Модели временных рядов
К этому классу относятся:
1.1. модели тренда:
,
где 
- временной тренд заданного параметрического вида;
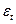- случайная (стохастическая) компонента;
1.2. модели сезонности:
,
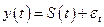где 
- периодическая (сезонная) компонента,
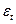- случайная (стохастическая) компонента;
1.3. модели тренда и сезонности:
(аддитивная) или
(мультипликативная).
К моделям временных рядов относится множество более сложных моделей, таких, как модели адаптивного прогноза, модели авторегрессии и скользящего среднего (ARIMA) и др. Их общей чертой является то, что они объясняют поведение временного ряда, исходя только из его предыдущих значений. Такие модели могут применяться, например, для изучения и прогнозирования объема продаж авиабилетов, спроса на мороженое, краткосрочного прогноза процентных ставок и т. п.
2. Регрессионные модели с одним уравнением
В таких моделях зависимая (объясняемая) переменная 
представляется в виде функции 
где 
- независимые (объясняющие) переменные, а 
- параметры. В зависимости от вида функции 
модели делятся на линейные и нелинейные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т. п.
Область применения таких моделей, даже линейных, значительно шире, чем моделей временных рядов. Проблемам теории оценивания, верификации, отбора значимых параметров и другим посвящен огромный объем литературы. Эта тема является, пожалуй, стержневой в эконометрике и основной в данном курсе
3. Системы одновременных уравнений
Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, мы имеем здесь набор объясняемых переменных, связанных через уравнения системы. Системы одновременных уравнений требуют относительно более сложный математический аппарат.
|
|
|
Таким образом, независимо от типа эконометрическая модельсостоит из входа – траектории внесистемных (экзогенных) переменных для всего исследуемого периода (инструментальных и заданных), начальных значений запаздывающих внутрисистемных переменных (начальных условий), выхода (значений целевых внутрисистемных переменных) и структуры (оператора преобразования входов в выход).
Структура состоит из регулярной части, с помощью которой описываются прогнозные величины, и случайной – возмущений. Предполагается, что на горизонте прогноза структура остается инвариантной. Регулярная часть структуры состоит из спецификации зависимостей, определяющей форму структуры уравнений, и оцениваемых статистических структурных коэффициентов.
Зависимости, входящие в эконометрическую модель, по характеру определяемых ими связей подразделяются на:
1) уравнения экономического поведения;
2) институциональные зависимости;
3) технологические зависимости;
4) тождества.
Уравнения экономического поведения выражают типы экономических решений, принимаемых определенными группами участников экономического процесса.
Институциональные зависимости отражают существующие законодательные или другие нормативные ограничения. Примером могут служить уравнения налоговых или таможенных сборов.
Технологические зависимости выражаются производственными функциями, отражающими технологию производственной системы в обобщенном, агрегированном виде.
Тождества (определяющие или балансовые) используются там, где переменные, согласно определению, заменяются одной, или вытекают из балансовых соотношений.
Процесс построения эконометрической модели состоит из следующих процедур:
1) неформальный анализ и диагностика объекта моделирования;
2) определение цели построения модели;
3) определение перечня переменных модели с разделением их на целевые, инструментальные и заданные;
4) спецификация модели – определение вида структурных уравнений;
|
|
|
5) выдвижение гипотез относительно вида распределений случайных величин, фигурирующих в модели;
6) построение временных рядов на основе прошлых наблюдений;
7) анализ временных рядов для определения наличия корреляционных и автокорреляционных зависимостей;
8) корректировка зависимостей, постулированных на этапе (4);
9) выбор метода оценивания структурных коэффициентов модели с учетом гипотез о вероятностных свойствах случайных возмущений и характера временных рядов;
10) оценивание структурных коэффициентов с помощью выбранного метода;
11) проверка качества полученных оценок;
12) проверка всей модели путем экстраполяции;
13) разработка неформальных сценариев развития событий на прогнозируемый период;
14) формализация сценариев в терминах инструментальных и заданных переменных, а также структурных коэффициентов;
15) имитация и последовательное (период за периодом) решение систем уравнений модели, получение многовариантного прогноза;
16) интерпретация полученных результатов, анализ и корректировка модели.
Эконометрические модели большой размерности получили широкое распространение во многих странах. Последовательно используются системы моделей в индикативном планировании в Японии и во Франции. В последнее время дескриптивные эконометрические модели используются в качестве системы ограничений для решения оптимальных задач, например, в Англии.
Центром научных исследований в области теории и техники эконометрического моделирования являются США. Американские модели, как правило, детализированные, многоотраслевые. В числе наиболее интересных следует отметить: The Brookinq quarterly econometric model (1965-1969 гг.); модель OBE Гарвардского университета (1969г.); динамические межотраслевые модели, разработанные К. Алмоном; серию уортонских моделей Л. Клейна и Р. Престона; энергетическую модель Б. Берненке и Д. Джоргенсона, модель финансовых потоков США Г. Фромма.
Эконометрические макромодели используются для изучения и прогноза межрегиональных связей в моделях глобального развития (система моделей японских ученых И. Кайа, Г. Сузуки, А. Ониши). Строятся эконометрические модели для изучения мировых рынков товаров (Кембридж, 1975).
|
|
|
Эконометрия имеет широкое поле применения: для измерения экономического развития, экономических циклов, величины спроса и предложения, эластичности спроса, издержек производства и темпов накопления, межотраслевых производственных связей.
|
|
|
