Линейный коэффициент корреляции

Линейный коэффициент корреляции указывает, есть ли между двумя рядами X и Y линейная зависимость и какой силы. Вычисляется по следующей формуле:

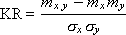
m_x, m_y, m_xy — математическое ожидание x, y, xy:

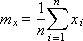
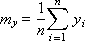
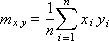
Дисперсия σ_x² и σ_y² показывает, насколько разбросаны точки от средней величины:

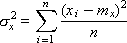
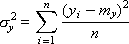
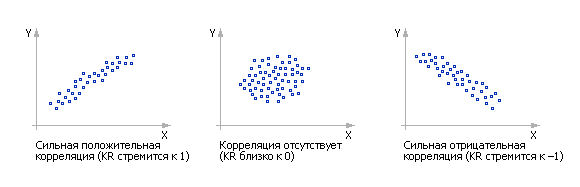
Линейный коэффициент корреляции может иметь знак плюс или минус. Положительная его величина свидетельствует о прямой связи между X и Y. Чем ближе KR к +1, тем связь более тесная. Отрицательная величина его свидетельствует об обратной связи; в этом случае границей является –1. Близость KR к нулю свидетельствует о слабой связи между X и Y (см. рис. 9.1).

Рис. 9.1.

Нелинейный коэффициент корреляции

Рис. 9.2.

Нелинейный коэффициент корреляции вычисляется по следующей формуле:

bug09.05. Проверить все эти формулы!!!

bug09.06. откуда берется "средняя величина"?

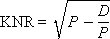
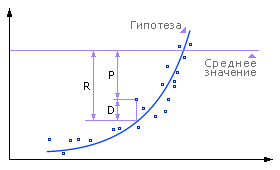
P — разброс между реальными точками и средней величиной: bug09.07. средним значением?

D — разброс между гипотетической кривой и реальными точками:

??

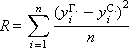
R — разброс между гипотезой и средней величиной:

??

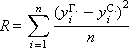
Коэффициент корреляции двух динамических рядов

X и Y представляются в виде рядов z_i и u_i для того, чтобы исключить постоянную составляющую: z_i = x_i – m_x
u_i = y_i – m_y

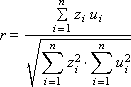
При r –> 1 имеет место тесная корреляция. При r –> 0 процессы взаимно ортогональны, корреляции нет, процессы не связаны друг с другом.

Bug09.09 Более ясные рисунки

Корреляция внутри динамического ряда

Исследуется сила связи между прошлым и настоящим одного процесса. Для этого сигнал сравнивают с самим собой, сдвинутым во времени, и вычисляют коэффициент корреляции двух динамических рядов (см. п. 3).

bug09.12. Неясный рисунок

Поиск периодичности ряда

Есть ли периодичность в динамическом ряду, можно выяснить, проделав прямое преобразование Фурье и рассмотрев спектр исследуемого сигнала. Об этом рассказывается в лекции 07 «Модель динамической системы в виде Фурье представления (модель сигнала)»

Зависимость динамики ряда Z от двух динамических факторов X и Y

Рис. 9.5.

Bug09.13. Неясные рисунки (их не надо)

Коэффициент множественной корреляции R:

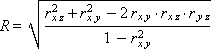
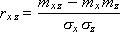
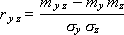
Связь двух признаков

Формула

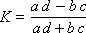
где K — это коэффициент ассоциаций, позволяет выяснить, имеется ли какая-либо связь между двумя признаками. Если данный коэффициент близок к единице, то в этом случае можно говорить о существовании такой связи.

Пример. Попытаемся с помощью данной формулы выяснить, есть ли связь между ростом и весом человека? Пусть в нашем распоряжении имеются данные о весе и росте 500 человек:

Таблица 9.1.

Вес < 67 кг. Вес > 67 кг. Рост < 167 см. a = 304 чел. b = 17 чел. Рост > 167 см. c = 112 чел. d = 67 чел.

По формуле: K = (304 · 67 – 17 · 112)/(304 · 67 + 17 · 112) = 0.83. Так как величина 0.83 близка к 1, то можно говорить о существовании определенной связи между весом и ростом.

Численные методы интегрирования
дифференциальных уравнений.
Метод Эйлера

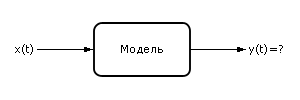
Пусть нам известна входная динамическая последовательность X (входной сигнал) и модель (способ преобразования входного сигнала в выходной сигнал). Рассматривается задача определения выходного сигнала y (t) (см. рис. 10.1).

Рис. 10.1. Структурная модель динамической системы с одним входом и одним выходом

Модель динамической системы может быть представлена дифференциальным уравнением. Основное уравнение динамики:

y' = f (x (t), y (t), t).

Известны начальные условия в нулевой момент времени t ₀: y (t ₀), x (t ₀). Чтобы определить выходной сигнал, заметим, что по определению производной:

Нам известно положение системы в точке «1», требуется определить положение системы в точке «2». Точки отделены друг от друга расстоянием Δ t (рис. 10.2). То есть расчет поведения системы производится по шагам. Из точки «1» мы скачком (дискретно) переходим в точку «2», расстояние между точками по оси t называется шагом расчета Δ t.

Рис. 10.2. Иллюстрация расчета будущего состояния системы методом Эйлера на одном шаге

Тогда:

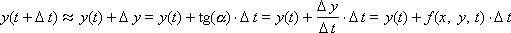
или

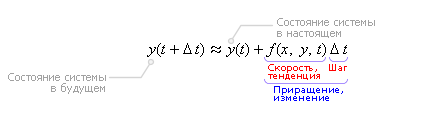
Последняя формула называется формулой Эйлера.

Очевидно, чтобы узнать состояние системы в будущем y (t + Δ t), надо к настоящему состоянию системы y (t) прибавить изменение Δ y, прошедшее за время Δ t.

будущее = настоящее + изменение

 

будущее = настоящее + скорость · шаг

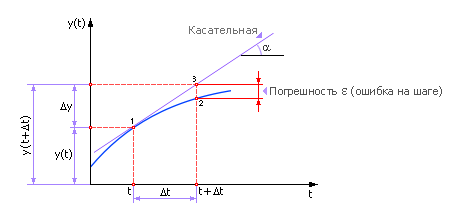
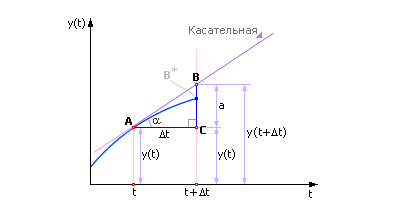
Рассмотрим еще раз это важное соотношение, выведя его из геометрических соображений (рис. 10.3).

Рис. 10.3. Геометрическая иллюстрация метода Эйлера

Пусть A — точка, в которой состояние системы известно. Это «настоящее» состояние системы.

В точке A к траектории движения системы проведем касательную. Касательная — это производная функции f (x (t), y (t), t) по переменной t. Производную в точке всегда легко вычислить, достаточно подставить известные переменные (в момент «Настоящее» они известны) в формулу y' = f (x (t), y (t), t).

Заметим, что, по определению, производная связана с углом наклона касательной: y' = tg(α), значит, угол α легко вычислить (α = arctg(y')) и провести касательную.

Проведем касательную до пересечения с линией t + Δ t. Момент t + Δ t соответствует «будущему» состоянию системы. Проведем линию параллельно оси t от точки A до пересечения с линией t + Δ t. Линии образуют прямоугольный треугольник ABC, один катет которого равен Δ t (известен). Известен также угол α. Тогда второй катет в прямоугольном треугольнике ABC равен: a = Δ t · tg(α). Теперь легко вычислить ординату точки B. Она состоит из двух отрезков — y (t) и a. Ордината символизирует положение системы в точке y (t + Δ t). То есть y (t + Δ t) = y (t) + a или далее y (t + Δ t) = y (t) + Δ t · tg(α) или, подставляя дальше, имеем: y (t + Δ t) = y (t) + Δ t · y' и, наконец, y (t + Δ t) = y (t) + Δ t · f (x (t), y (t), t). Снова мы получили формулу Эйлера (из геометрических соображений).

Эта формула может дать точные результаты только при очень малых Δ t (говорят при Δ t –> 0). ПриΔ t ≠0 формула дает расхождение между истинным значением y и расчетным, равное ε, поэтому в ней должен стоять знак приближенного равенства, либо она должна быть записана так:

y (t + Δ t) = y (t) + Δ t · f (x (t), y (t), t) + ε.

И в самом деле. Взгляните еще раз на рис. 10.3. Будем мысленно сдвигать линию t + Δ t влево (фактически, будем приближать значение Δ t к нулю). Как нетрудно видеть, расстояние BB^* = ε, — то есть ошибка! — будет сокращаться. В пределе (при Δ t –> 0) значение ошибки ε будет равно нулю.

Итак, заменяя реальную кривую прямой (касательной) на отрезке Δ t, мы вносим в решение ошибку, попадая в результате не в точку «2» (см. рис. 10.2), а рядом, в точку «3». Очевидно, что этот численный метод на каждом шаге имеет погрешность расчета ε.

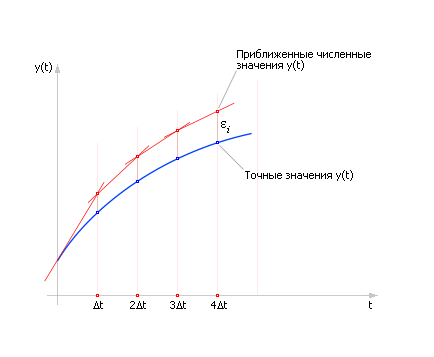
Из рисунка видно, что чем меньше взять величину Δ t, тем меньше будет ошибка расчета ε. То есть для расчета поведения системы на сколько-нибудь продолжительном отрезке времени (например, от t ₀ до t_k), чтобы уменьшить ошибку на каждом шаге, шаги Δ t делают по возможности малыми. Для достижения точки t_k отрезок (t_k – t ₀) делится на отрезки длиной Δ t; таким образом, всего получится N = (t_k – t ₀)/Δ t шагов. В результате расчета придется формулу Эйлера применить для каждого шага, то есть N раз. Но следует иметь в виду, что ошибки ε_i на каждом i -ом шаге (в простейшем случае) складываются, а общая ошибка быстро накапливается (см. рис. 10.4). И в этом состоит существенный недостаток данного метода. Хотя с помощью этого метода можно получить (в численном виде) решение любого дифференциального уравнения (в том числе и неразрешимого аналитически). Уменьшая шаг, мы получаем более точные решения, но при этом не следует забывать, что увеличение числа шагов ведет к вычислительным затратам и снижению быстродействия. Кроме того, при большом числе итераций в расчет вносится другая существенная погрешность из-за ограниченной точности вычислительных машин и ошибок округления.

Рис. 10.4. Нарастание суммарной ошибки в методе Эйлера на ряде шагов

Задача 1. Дано дифференциальное уравнение y' = 2 ty. Задано начальное положение системы: y (0) = 1. Требуется найти y (t), то есть поведение системы на интервале времени t от 0 до 1.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: