1.4. Основные законы электрической цепи

1. 4. Основные законы электрической цепи

 

1. 4. 1. Закон Ома для электрической цепи, не содержащего ЭДС

 

Закон Ома для участка цепи, не содержащего ЭДС, устанавливает связь между током и напряжением на этом участке. Применительно к рис. 1. 4 а запишем

 

 или .

 

 

1. 4. 2. Закон Ома для электрической цепи, содержащего ЭДС

 

Закон Ома для участка цепи, содержащего ЭДС, позволяет найти ток этого участка по известной разности потенциалов на концах участка цепи и имеющейся на этом участке ЭДС Е. Так, для схемы рис. 1. 4 б

 

.

 

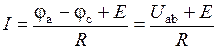Аналогично для схемы рис. 1. 4 в

 

.

 

В общем случае

 

.

 

Знак «плюс» перед E ставится в том случае, если направление тока и направление ЭДС совпадают.

1. 4. 3 Законы Кирхгофа для линейных электрических цепей

 

Сложная электрическая цепь характеризуется следующими понятиями: ветвь, узел, контур.

Ветвь – участок электрической цепи, по которому протекает один и тот же ток.

Узел – место соединения не менее трех ветвей электрической цепи.

Контур – замкнутый путь, проходящий по ветвям электрической цепи.

Первый закон Кирхгофа. Алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:

 

                                        .                                            (1. 4)

 

Для электрической цепи, содержащей y узлов, по первому закону Кирхгофа составляется y – 1 независимых уравнений для любых выбранных y – 1 узлов. Для последнего узла уравнение является зависимым, т. е. его можно получить из предыдущих уравнений. Направление токов в ветвях цепи выбирают произвольно; токи, направленные к узлу, берут с одним знаком, например плюс (+), а токи, направленные от узла, – с другим знаком, например, минус (–).

Первый закон Кирхгофа является следствием непрерывности тока и неизменности зарядов в узлах электрической цепи.

Второй закон Кирхгофа. Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС в этом контуре:

 

                                    .                                     (1. 5)

 

В каждом контуре произвольно выбирают направление обхода контура. Напряжения и ЭДС в уравнении (1. 5) берут с положительным знаком, если направление напряжений, ЭДС и токов совпадает с направлением обхода контура.

При расчете электрической цепи число неизвестных токов равно числу ветвей в цепи b. Составив по первому закону Кирхгофа y – 1 уравнение, по второму закону Кирхгофа остается составить k = b – y + 1 уравнений (по числу независимых контуров). Независимыми контурами называются такие контура, в которые входит хотя бы одна ветвь, не входящая в предыдущие контура.

При определении числа ветвей b не учитывают ветви с R = 0, а ветви с одним и тем же током принимают за одну ветвь. При определении числа узлов y учитывают только те узлы, в которых сходится более чем две ветви, а ветви с сопротивлением R = 0 включают в состав узла.

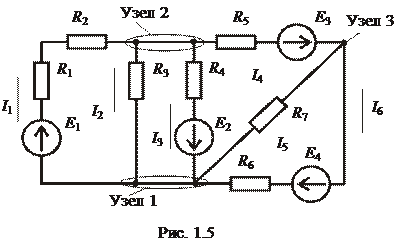Пример. Для электрической цепи рис. 1. 5 записать уравнения по законам Кирхгофа.

Электрическая цепь содержит 6 ветвей, 3 узла. Направления токов в ветвях выбрано произвольными. Всего требуется записать 6 независимых уравнений для определения токов во всех ветвях. Для двух любых узлов, например, 1 и 3, по первому закону Кирхгофа составляем два уравнения. Втекающие в узел токи возьмем со знаком плюс.

Для узла 1: –I₁ + I₂ – I₃ – I₅ + I₆ = 0.

Для узла 3: –I₄ + I₅ – I₆ = 0.

По второму закону Кирхгофа для 4 независимых контуров запишем уравнения. Направление обхода контуров выберем по часовой стрелке. В электрической цепи можно выделить 4 независимых контура, например: 1-й контур – E₁ – R₁ – R₂ – R₃, 2-й контур – R₃ – R₄ – E₂, 3-й контур – E₂ – R₄ – R₅ – E₃ – R₂, 4-й контур – R₇ – E₄ – R₆.

Для 1 – го контура: (R₁ + R₂) ∙ I₁ + R₃ ∙ I₂ = E₁.

Для 2 – го контура: – R₃ ∙ I₂ – R₃ ∙ I₃ = E₂.

Для 3 – го контура: R₄ ∙ I₃ – R₅ ∙ I₄ – R₇ ∙ I₅ = – E₂ + E₃.

Для 4 – го контура: R₇ ∙ I₅ + R₆ ∙ I₆ = E₄

При вычислении токов в ветвях электрической цепи удобнее пользоваться матричной формой записи уравнений Кирхгофа:

 

                                           A ∙ I = B ∙ E,                                      (1. 6)

 

где A, B – квадратные матрицы коэффициентов при токах и напряжениях порядка b× b; I, E – матрицы – столбцы неизвестных токов и заданных ЭДС.

Элементами матрицы А являются коэффициенты при токах в левой части уравнений, составленных по первому и второму законам Кирхгофа. Первые y – 1 строк матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, –1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.

Элементы следующих b – y + 1строк матрицы А равны значениям сопротивлений при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком.

Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые y – 1 строк матрицы имеют нулевые элементы, так как ЭДС в правой части уравнений, записанных по первому закону Кирхгофа, отсутствуют. Остальные b – y + 1 строки содержат элементы +1, –1 в зависимости от того, с каким знаком входит ЭДС в уравнение, и 0, если ЭДС в уравнение не входит.

Общее решение уравнений, составленных по законам Кирхгофа:

                                        I = (A^-1B)∙ E = GE                                 (1. 7)

 

где                                                       G = A^-1B – матрица проводимостей;

 

                                               (1. 8)

 

Токи в каждой ветви:

 

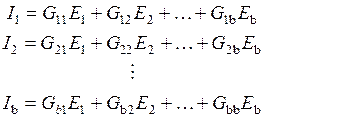                                         (1. 9)

 

Пример. Для схемы рис. 1. 5 записать уравнения по законам Кирхгофа в матричной форме записи. По первому закону Кирхгофа составлены два уравнения для узлов 1 и 3

 

– I₁ + I₂ – I₃ – I₅ + I₆ = 0; – I₄ + I₅ – I₆ = 0.

 

По второму закону Кирхгофа записываются 4 уравнения для контуров

 

(R₁ + R₂) ∙ I₁ + R₃ ∙ I₂ = E₁; – R₃ ∙ I₂ – R₃ ∙ I₃ = E₂; R₄ ∙ I₃ – R₅ ∙ I₄ – R₇ ∙ I₅ = – E₂ + E₃; R₇ ∙ I₅ + R₆ ∙ I₆ = E₄

 

В матричной форме записи

 

A ∙ I = B ∙ E,

 

где

; ;

 

;           .

 

 

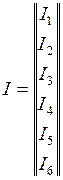1. 5. Методы расчета электрических цепей

 

1. 5. 1. Метод контурных токов

 

Уравнения Кирхгофа позволяют рассчитать электрическую любую цепь, но при этом число решаемых уравнений может быть велико. Для сокращения числа решаемых уравнений рационализируют составление и решение уравнений Кирхгофа, применяя для расчета метод контурных токов, узловых потенциалов. Метод основан на применении второго закона Кирхгофа и позволяет сократить при расчете сложных систем число решаемых уравнений. Во взаимно независимых контурах, где для каждого контура хотя бы одна ветвь входит только в этот контур, рассматривают условные контурные токи во всех ветвях контура. Контурные токи в отличие от токов ветвей имеют свои индексы и их направление в контуре целесообразно выбирать одинаковым, например, по часовой стрелке. Уравнения составляют по второму закону Кирхгофа для контурных токов. Токи ветвей выражают через контурные токи по первому закону Кирхгофа. Число выбираемых контуров и число решаемых уравнений равно числу уравнений, составляемых по второму закону Кирхгофа: k = b – y + 1. Сумма сопротивлений всех резистивных элементов каждого контура со знаком плюс является коэффициентом при токе контура. Знак коэффициента при токе смежных контуров зависит от совпадения или несовпадения направления смежных контурных токов. ЭДС входит в уравнение со знаком плюс, если направление ЭДС и направление тока контура совпадают.

Пример. Записать уравнения по методу контурных токов для схемы рис. 1. 6.

Схема содержит шесть ветвей (b = 6) с неизвестными токами и три узла (y = 3). Так как k = b – y + 1 = 4, то предпочтителен метод контурных токов. Для четырех контуров с токами I_k1, I_k2, I_k3, I_k4 записывают уравнения по второму закону Кирхгофа:

 

    (1. 10)

 

где R₁₁ = R₁ + R₂ + R₃, R₂₂ = R₃ + R₄, R₃₃ = R₄ + R₅ + R₇, R₄₄ = R₆ + R₇ – полное сопротивление соответствующих контуров; R₁₂ = R₂₁ = R₃, R₂₃ = R₃₂ = R₄, R₃₄ = R₄₃ = R₇ – сопротивление ветвей связи первого контура со вторым R₁₂, второго с первым R₂₁ и так далее E₁₁ = E₁, E₂₂ = E₂, E₃₃ = – E₂ + E₃, E₄₄ = E₄ – полные ЭДС контуров.

Токи ветвей (смотри их обозначение на рис. 1. 5) определяются по первому закону Кирхгофа. Например, в ветви с сопротивлениями R₁, R₂ протекающий снизу вверх ток I₁ равен контурному току I₁ = I_k1, в ветви с сопротивлением R₃ протекающий сверху вниз ток равен разности токов

 

I₂ = I_k1 – I_k2, I₃ = – I_k2 + I_k3, I₄ = – I_k3, I₅ = – I_k3 + I_k4, I₆ = – I_k4.

 

Если в электрической цепи будет иметься n независимых контуров, то количество уравнений будет равно n.

Общее решение системы n уравнений относительно тока I_kk

 

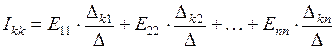                 .              (1. 11)

Здесь  – определитель системы.

 

                                                    (1. 12)

 

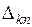 – есть алгебраическое дополнение, полученное из определителя  путем вычеркивания k столбца и n строки и умножения полученного определителя на (–1)^{k + n}.

В матричной форме записи уравнение (1. 9) имеет вид R_k∙ I_k = E_k; I_k = G_k∙ E_k = R_k^–1∙ E_k и являются общей матричной формой записи и решения уравнений по методу контурных токов.

 

1. 5. 2. Метод узловых потенциалов

 

Метод основан на применении первого закона Кирхгофа и позволяет сократить число решаемых уравнений при нахождении неизвестных токов до y – 1. Ток в любой цепи может быть найден по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, надо знать потенциалы узлов. Допустим, что в схеме y узлов. Так как любая (одна) точка схемы может быть заземлена без изменения токораспределения в схеме, то мы вправе один из узлов схемы мысленно заземлить, т. е. принять потенциал его равным нулю. При этом число неизвестных уравнений уменьшить с y до y – 1. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые надо составить для схемы по первому закону Кирхгофа. Обратимся к схеме на рис. 1. 7. Схема имеет три узла и шесть ветвей. Если один узел схемы, например узел 1, мысленно заземлить, т. е. принять 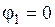, то необходимо будет определить потенциалы только двух узлов . Для единообразия в обозначениях условимся, что проводимости ветвей будем снабжать двумя индексами, номерами узлов, к которым подключена ветвь.

В соответствии с обозначениями токов составим уравнения по первому закону Кирхгофа для второго узла:

 

I₁ – I₂ + I₃ + I₄ = 0,

 

или

 

Перепишем последнее уравнение следующим образом:

 

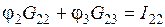                                                                   (1. 13)

 

Здесь:    ;

 

;

 

.

 

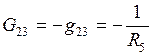Обсудим структуру уравнения (1. 13). Множителем при 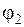 в нем является коэффициент G₂₂, равный сумме проводимостей всех ветвей, сходящихся ко второму узлу. Проводимость G₂₃ равняется сумме проводимостей ветвей, соединяющих узел 2 с узлом 3, взятой со знаком «минус» (в нашем случае проводимость одной ветви). Ток I₂₂ называется узловым током второго узла. Это расчетная величина, равная алгебраической сумме токов, полученной от деления ЭДС ветвей, подходящих к узлу 2, на сопротивления данных ветвей. В эту сумму со знаком «плюс» входят токи тех ветвей, ЭДС которых направлены к узлу 2.

Подобное уравнение может быть записано и для 3 узла схемы. Если схема имеет y узлов, то ей соответствует система (y – 1) уравнений вида

(1. 14)

 

где G_kk – сумма проводимостей ветвей, сходящихся в узле k;

G_km – сумма проводимостей ветвей, соединяющих узлы k и m, взятая со знаком «минус»;

I_kk – узловой ток k узла.

Если к k – узлу подтекает ток от источника тока, то он должен быть включен в ток I_kk со знаком «плюс», если утекает, то со знаком «минус».

Если между какими – либо двумя узлами нет ветвей, то соответствующая проводимость равна нулю. После решения системы уравнений (1. 14) относительно потенциалов определяют токи в ветвях по закону Ома для участка цепи, содержащего ЭДС.

Формула двух узлов. Очень часто встречаются схемы, содержащие всего два узла. Наиболее рациональным методом расчета токов в них является метод, получивший название метода двух узлов.

Под методом двух узлов понимают метод расчета электрической цепи, в котором за искомое (через него определяют затем токи ветвей) понимают напряжение между двумя узлами схемы.

Расчетные формулы этой схемы непосредственно следуют из более общего метода – метода узловых потенциалов.

Напряжение между двумя узлами может быть найдено

 

                                                                                     (1. 15)

 

После того как напряжение U_ab будет найдено, определяется ток в любой ветви по формуле:

 

I_k = (± E_k ± U_ab) ∙ g_k.

 

Пример. Найти токи в схеме рис. 1. 8, если E₁ = 120 В, E₃ = 50 В, R₁ = 2 Ом, R₂ = 4 Ом, R₃ = 1 Ом, R₄ = 10 Ом

Решение.

 

 

 

 

.

 

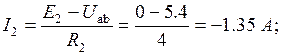
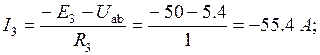
⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: