 |
3.1 методы анализа
|
|
|
|
Переходный процесс возникает непосредственно после скачкообразного изменения параметра электрической цепи. Например, подводимого к электрической цепи напряжения, сопротивления резистора, индуктивности катушки индуктивности, емкости конденсатора и т. п. Чаще всего переходный процесс наступает при срабатывании коммутирующих элементов цепи. При переходных процессах могут возникать большие напряжения и токи, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах сигналов. Все это приводит к необходимости изучения методов анализа переходных режимов работы цепи.
Можно назвать следующие основные методы анализа переходных процессов в линейных цепях.
Классический метод предполагает составление дифференциального уравнения для интервала времени t ≥ 0, который не включает момент скачкообразного изменения параметра цепи. Считается, что в момент времени t = 0 это изменение уже произошло и с этого момент начинается переходный процесс. Решение уравнения осуществляется путем его непосредственного интегрирования при начальных условиях, заданных для t = 0. Этими начальными условиями фактически и определяется характер переходного процесса.
Метод, отличающийся от классического использованием преобразования Лапласа для решения дифференциального уравнения.
Третий метод используется, когда скачкообразно изменяется напряжение или ток некоторого источника на интервале t ≥ 0. Предполагается, что все напряжения и токи в цепи равны нулю при t < 0. Дифференциальное уравнение составляется для интервала времени − ∞ < t < ∞. Для решения уравнения используется преобразование Лапласа.
|
|
|
Четвертый метод используется при скачкообразном изменении напряжения или тока источника на интервале − ∞ < t < ∞. Предполагается, что все напряжения и токи в цепи представляют собой абсолютно интегрируемые функции времени. Дифференциальное уравнение составляется для интервала времени − ∞ < t < ∞. Для решения уравнения используется преобразование Фурье.
В данном разделе рассматривается классический метод анализа переходных процессов, а другие методы будут изложены в последующих двух разделах.
3. 2 Дифференциальные уравнения
Классический метод анализа переходных процессов заключается в непосредственном решении дифференциального уравнения, описывающего изменение тока или напряжения на участке цепи. При этом используются законы Кирхгофа для мгновенных значений напряжений и токов, а также следующие соотношения, связывающие между собой напряжения uR, uL и uC на R, L и C – элементах и токи iR, iL и iC в этих элементах:
, 
, 
.
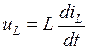Здесь R, L и C – сопротивление, индуктивность и емкость R, L и C – элемента и предполагается, что для токов и напряжений на элементах выбраны совпадающие положительные направления. Практически любой переходный процесс можно исследовать, используя в схеме замещения идеальные коммутирующие элементы. При этом наиболее часто используются элементы, приведенные на рис. 3. 1. На рис. 3. 1 а показан элемент с нормально разомкнутыми контактами, на рис. 3. 1 б – элемент с нормально замкнутыми контактами, а на рис. 3. 1 в – с переключаемыми контактами. Идеальность этих элементов заключается в том, что сопротивление между разомкнутыми контактами равно бесконечности, а сопротивление между замкнутыми контактами равно нулю.
Пусть задана цепь, схема которой приведена на рис. 3. 2. Здесь и далее U – постоянное во времени напряжение. Необходимо составить дифференциальное уравнение, описывающее переходный процесс после замыкания контактов коммутирующего элемента.
|
|
|
Для интервала времени t ≥ 0 (контакты коммутирующего элемента замкнуты) запишем одно уравнение по первому закону Кирхгофа и два уравнения по второму закону Кирхгофа:
,
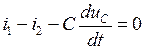, (3. 1)
.
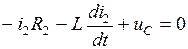Выразим i1из второго уравнения и uC из третьего и подставим в первое. После несложных преобразований можно получить
. (3. 2)
В общем случае уравнение, описывающее переходный процесс в цепи при t ≥ 0, имеет вид:
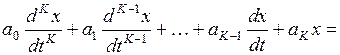
, (3. 3)
где х – искомая функция времени (напряжение, ток); f – известная функция времени (ее вид определяется параметрами источника электрической энергии); a1, a2, …, aK, b1, b2, …, bM – постоянные коэффициенты, определяемые параметрами цепи. Порядок данного уравнения K равен числу L – элементов и C – элементов в упрощенной схеме, получаемой из исходной путем эквивалентного преобразования в один элемент L – элементов, соединенных последовательно, и C – элементов, соединенных параллельно. Как известно из математики, общее решение x уравнения (3. 3) представляет собой сумму частного решения исходного неоднородного уравнения xв и общего решения xсв соответствующего однородного уравнения, т. е. x = xв + xсв. Частное решение принято называть вынужденной составляющей решения. Эта составляющая определяется видом функции f в его правой части. Если f – постоянная во времени величина или изменяющаяся по синусоидальному закону функция времени, то и вынужденная составляющая ищется в виде постоянной величины или в виде синусоидально изменяющейся функции времени. Вынужденная составляющая в виде постоянной величины легко определяется непосредственно из дифференциального уравнения, поскольку при этом все производные равны нулю. Вынужденная составляющая в виде синусоидальной функции также может быть определена из дифференциального уравнения, однако проще это сделать комплексным или символическим методом.
|
|
|
Вторая составляющая xсв общего решения, называется свободной. Определение свободной составляющей зависит от вида корней характеристического уравнения. Например, если корни p1, p2, …, pk, различные, то
.
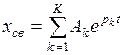Здесь A1, A2, …, Ak – постоянные интегрирования, которые в дальнейшем определяются из начальных условий. Если среди корней имеются пары комплексно сопряженных корней вида pk = δ k + jω k, pk+1 = δ k - jω k, то каждой такой паре будет соответствовать слагаемое вида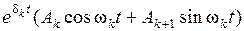 
.
Необходимо помнить, что, в устойчивой линейной цепи с течением времени свободная составляющая затухает, поэтому вещественные части корней характеристического уравнения не могут быть положительными. При вещественных корнях xсв монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс). Таким образом, переходный процесс в цепи определяется наложением двух составляющих – вынужденной, возникающей как бы сразу после коммутации, и свободной, имеющей место только в течение переходного процесса. С течением времени свободная составляющая стремится к нулю, переходный процесс заканчивается и наступает установившийся режим работы цепи, характеризующийся наличием только вынужденной составляющей.
3. 3 Начальные условия. Законы коммутации
В общее решение уравнения (3. 3) входят постоянные интегрирования, число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся токи в L – элементах и напряжения на C – элементах в момент времени t = 0 (момент коммутации). Независимые начальные условия определяются на основании законов коммутации исходя из значений токов в L – элементах и напряжений на C – элементах в момент времени, непосредственно предшествующий коммутации, t = 0 –.
Первый закон коммутации – ток в L – элементе в момент коммутации iL(0)сохраняет значение до коммутации iL(0 –), т. е. iL(0) = iL(0 –).
|
|
|
Второй закон коммутации – напряжение на C-элементе в момент коммутации uC(0) сохраняет свое значение до коммутации uC(0 –), т. е uC(0) = uC(0 –)
Зависимыми начальными условиями называются значения остальных токов и напряжений и их производных в момент коммутации. Эти начальные условия определяются по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для t = 0. Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (3. 3) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (K-1) порядка включительно при t = 0.
Пусть для уравнения (3. 2) требуется определить начальные условия: i(0) и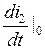 
. Будем считать до коммутации uC(0 –) = 0 и в цепи имел место установившийся режим, тогда 
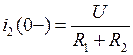. В соответствии с законами коммутации uC(0) = uC(0 –) = 0 и 
. Тогда из третьего уравнения системы (3. 1)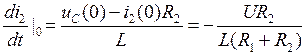 
.
3. 4 Замыкание цепи, содержащей R и L – элементы
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т. п. Определим переходный процесс после замыкания контактов коммутирующего элемента (t ≥ 0) в цепи, схема которой изображена на рис. 3. 3. По второму закону Кирхгофа uL + R = u. Имея в виду, что 
, дифференциальное уравнение, описывающее переходный процесс, имеет вид
.
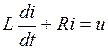Как было сказано выше, решение этого уравнения ищется в видеi = iв + iсв. Сначала определим свободную составляющую тока путем решения однородного уравнения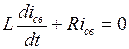 
. Для этого составим характеристическое уравнение Lp + R = 0, откуда 
, где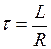 
- постоянная времени цепи. Тогда 
.
Далее рассмотрим два случая: u = U и Um sin(ω t + γ u). Здесь Um – амплитуда, γ u – начальная фаза синусоидального напряжения. В первом случае вынужденную составляющую тока будем искать в виде постоянной величины. Для вынужденной составляющей исходное дифференциальное уравнение запишется в виде 
. Учитывая, что 
, вынужденная составляющая 
. Таким образом, 
. Будем считать, что i(0− ) = 0. В соответствии с первым законом коммутации i(0) = i(0− ) = 0. Тогда 
, откуда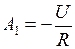 
. Таким образом, ток в цепи 
, напряжение на L – элементе 
.
Качественный вид кривых iв, iсв, i и uL, соответствующих полученным решениям, представлен на рис. 3. 4.
Во втором случае вынужденная составляющая тока рассчитывается с использованием символического метода. Комплексная амплитуда вынужденной составляющей тока
|
|
|
,
где 
. Тогда iв = Imвsin(ω t + γ u − φ ), 
. Постоянная интегрирования определяется из уравнения i(0) = Imвsin(γ u − φ ) + A1. Поскольку i(0) = 0, то A1 = − Imвsin(γ u − φ ). Окончательно получаем
.
Анализ полученного выражения показывает следующее. Во-первых, при γ u − φ = ±π переходного процесса нет, и в цепи сразу возникнет установившийся режим. Во-вторых, при 
и достаточно большой величине t, такой что за полпериода свободная составляющая существенно не уменьшается, максимальная величина тока переходного процесса может существенно превышать амплитуду тока установившегося режима.
Этот случай поясняется на рис. 3. 5 из которого видно, что максимум тока imax имеет место примерно через время, равное половине периода вынужденной составляющей. В пределе при τ → ∞ imax = 2Imв.
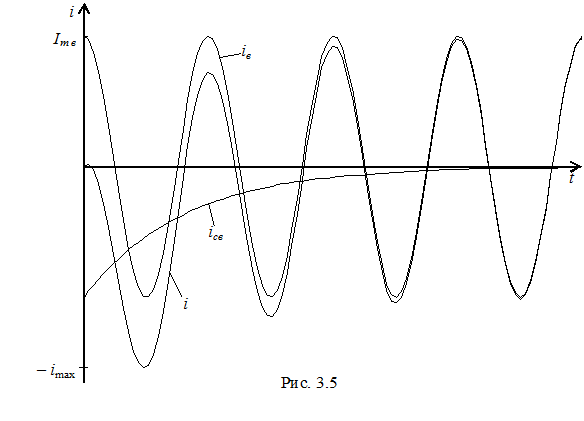
Можно показать, что для любой линейной цепи, содержащей только R и L – элементы, максимальное значение тока через L – элемент в переходном режиме при подключении цепи к синусоидальному источнику напряжения не превышает удвоенной амплитуды вынужденного тока.
Аналогично, для линейной цепи, содержащей только R и C – элементы, максимальное значение напряжения на C – элементе в переходном режиме при подключении цепи к синусоидальному источнику напряжения не превышает удвоенной амплитуды вынужденного напряжения.
3. 5 Размыкание цепи, содержащей R – и L – элементы
Рассмотрим переходный процесс в цепи, схема которой приведена на рис. 3. 6, после размыкания контактов коммутирующего элемента (t ≥ 0). Нетрудно получить дифференциальное уравнение, описывающее переходный процесс:
.
Решение этого уравнения ищется в виде I = iс + iсв. Вынужденная составляющая тока iсв = 0.
Для определения свободной составляющей составим характеристическое уравнение Lp + R1 + R2 = 0, откуда 
, где 
. Тогда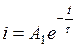 
. Предполагая, что 
, в соответствии с первым законом коммутации 
, тогда 
. Таким образом, ток в цепи 
, напряжение 
. Анализ этого выражения показывает, что при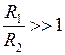 
напряжение на разомкнутых контактах в момент коммутации, равное 
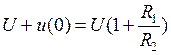, будет во много раз превышать напряжение источника. При достаточно большом значении R1 указанное напряжение может вызвать дугу и вывести из строя коммутирующий элемент.
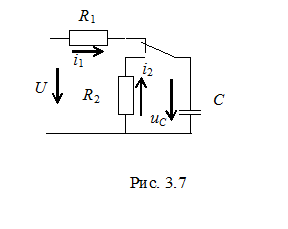
3. 6 Цепь из R – и C – элементов
Рассмотрим схему цепи на рис. 3. 7. При переводе контакта коммутирующего элемента из нижнего положения в верхнее начинается переходный процесс, связанный с зарядом C – элемента. Дифференциальное уравнение, описывающее этот процесс (t ≥ 0), можно получить в виде
. 
(3. 4)
Решение этого уравнения uC = uвС + uсвС.
Вынужденная составляющая напряжения на C – элементе uвС = U. Для определения свободной составляющей имеем характеристическое уравнение R1Cp + 1 = 0. Корень этого уравнения 
, где τ 1 = R1C − постоянная времени заряда. Тогда 
, 
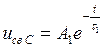. Предположим, что при t = 0 – напряжение на C – элементе не равно нулю, поскольку к моменту коммутации он мог разрядиться не полностью. Тогда A1 = uC (0) − U и
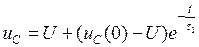(3. 5)
Ток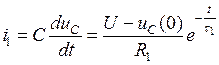 
.
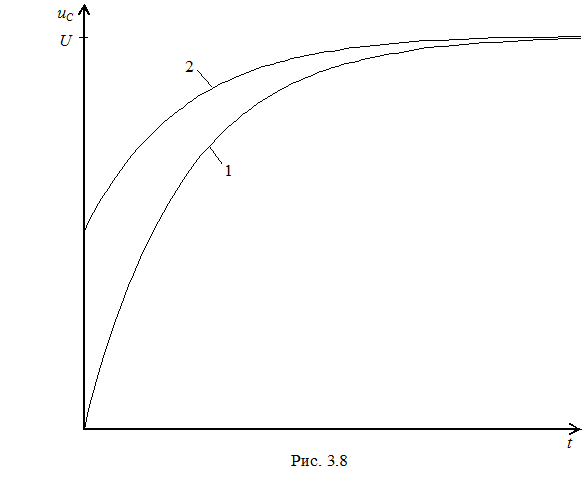
Кривые 1 и 2, изображенные на рис. 3. 8, поясняют характер переходных процессов при начальных условиях uC(0) = 0 и uC(0) > 0 соответственно.
При переводе контакта коммутирующего элемента из верхнего положения в нижнее (по рис. 3. 4) начинается переходный процесс, связанный с разрядом C – элемента. Дифференциальное уравнение, описывающее этот процесс (иС = 0)
.
Решение этого уравнения иС = ивС + иС. Нетрудно показать, что вынужденная составляющая, ивС = 0 а свободная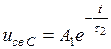 
, где τ 2 = R2C – постоянная времени разряда. Тогда, принимая, что к моменту коммутации C – элемент был заряжен до напряжения uC(0), можно записать
, 
.
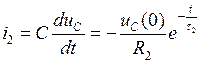Характер переходных процессов поясняется на рис. 3. 9, где кривые 1 и 2 соответствуют иС(0) = 0 и иС(0) > 0.
3. 7 Цепь из R, L и C – элементов
Рассмотрим цепь, схема которой приведена на рис. 3. 10.
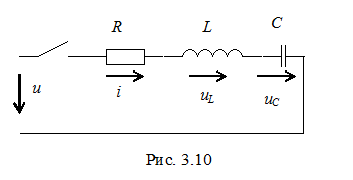На основании второго закона Кирхгофа после замыкания контактов коммутирующего элемента (t ≥ 0) 
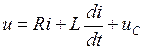. Подставив в это уравнение значение тока через C – элемент 
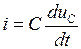, получим линейное дифференциальное уравнение второго порядка относительно uC:
.
Согласно изложенной ранее методике расчета переходных процессов классическим методом для напряжения на C – элементе можно записать иС = ивС + исвС. Для нахождения свободной составляющей составим характеристическое уравнение LCp2 + RCp + 1 = 0, решая которое, получаем
,
где 
– коэффициент затухания; 
- резонансная частота.
Здесь возможны два основных варианта. Во-первых,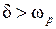 
, когда свободный процесс носит апериодический характер. При этом 
.
Во-вторых, 
, когда имеет место колебательный характер переходного процесса. При этом p1 = – δ + jω 0, p2 = – δ – jω 0, где 
– угловая частота собственных колебаний. Тогда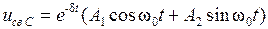 
.
Далее рассмотрим два случая: u = U и и = Umsin(ω t + γ и) Для первого случая вынужденная составляющая uвС = U. При апериодическом характере переходного процесса можно записать
. (3. 6)
Будем считать нулевыми независимые начальные условия, т. е. uC(0) = 0 и i(0) = 0. На основании равенства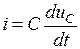 
можно записать зависимое начальное условие 
. Для нахождения постоянных интегрирования необходимо воспользоваться выражением (3. 6) и производной от этого выражения: 
. На основании (3. 6) и последнего выражения запишем для t = 0 два уравнения:
0 = U + A1 + A2;
.
Решая эти уравнения совместно, найдем постоянные интегрирования
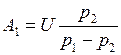и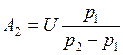 
. Подставив A1 и A2 в (3. 6), получим 
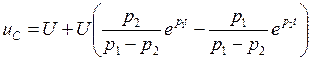. Тогда ток в цепи 
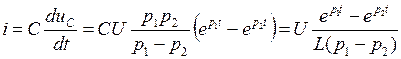. Напряжение на L – элементе 
.
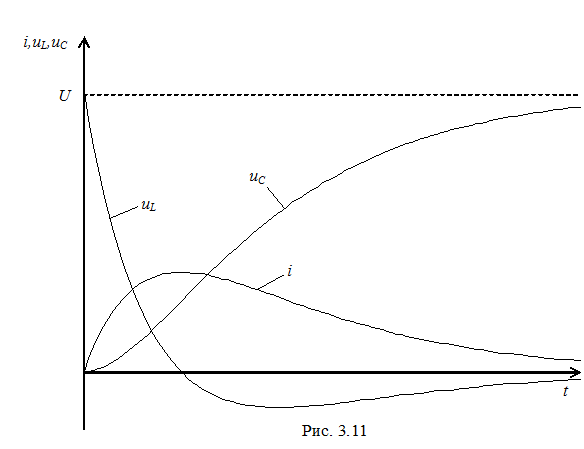
На рис. 3. 11 представлены качественные кривые uC, i и uL, соответствующие апериодическому переходному процессу.
При колебательном переходном процессе uC = U + e-δ t (A1cosω 0t + A2sinω 0t) Для нахождения постоянных интегрирования, имея в виду uC(0) = 0 и 
, запишем для t = 0 два уравнения:
0 = U + A1;
0 = –δ A1 + ω 0A2,
решая которые, получим A1 = –U; 
. Тогда
,
,
.
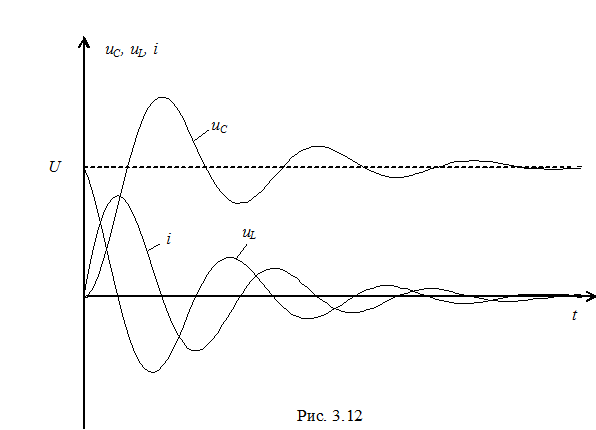
На рисунке 3. 12 представлены качественные кривые i, uC, uL, соответствующие колебательному переходному процессу.
Во втором случае при подключении цепи к источнику синусоидального напряжения для нахождения вынужденных составляющих тока в цепи и напряжения на C – элементе и L – элементе следует воспользоваться символическим методом расчета, в соответствии с которым
,
где
; 
.
Попутно заметим, что в данной цепи возможно явление резонанса при частоте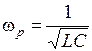 
, поскольку на этой частоте отсутствует фазовый сдвиг (φ = 0) между током iв и напряжением u.
Далее получим
,
,
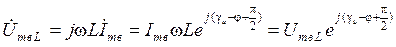где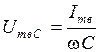 
, 
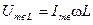. Переходя к синусоидальным выражениям, можно записать
, 
,
.
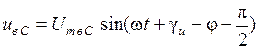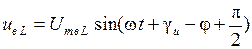Здесь также возможен апериодический режим и колебательный режимы. Наибольший интерес представляет колебательный режим, связанный с появлением во время переходного процесса собственных колебаний с частотой ω 0. При этом:
.
Исходя из этого выражения, для нахождения постоянных интегрирования, имея в виду uC(0) = 0 и 
, запишем для t = 0 два уравнения:
;
,
решая которые, при 
получим 
; 
. Тогда
,
,
.
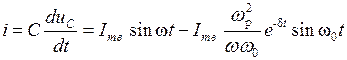При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, следующие характерные варианты: ω значительно меньше ω 0; ω несколько меньше ω 0; ω = ω 0; ω несколько больше ω 0; ω значительно больше ω 0. Эти варианты представлены на рис. 3. 13 … 3. 17 соответственно.
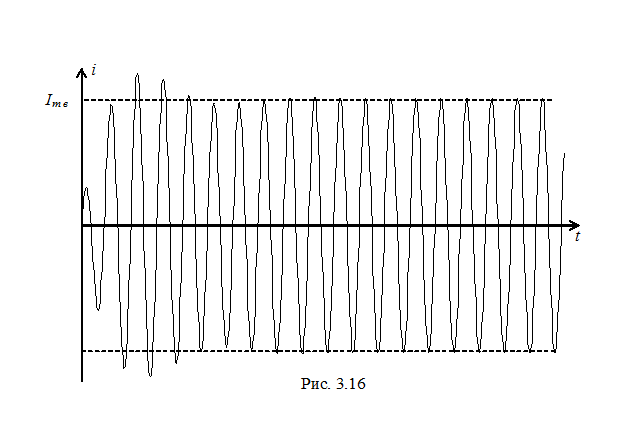
3. 8 Вопросы и задания для самопроверки
В результате чего возникают переходные процессы?
Дайте краткую характеристику классического метода анализа переходных процессов.
Как с использованием идеальных коммутирующих элементов отразить причины возникновения переходных процессов на схеме замещения?
Приведите соотношения между током и напряжением на R –, L – и C – элементах.
Как определить порядок дифференциального уравнения, описывающего цепь?
Сформулируйте законы коммутации.
Для какого момента времени и как определяются зависимые и независимые начальные условия?
Нарисуйте схему цепи, имеющей 2 узла, 3 ветви, источник ЭДС, R –, L, – C-элементы и коммутирующий элемент, составьте дифференциальное уравнение, описывающее переходный процесс.
Для предыдущего задания определите начальные условия, необходимые для решения дифференциального уравнения.
Каковы особенности переходных процессов в цепях, содержащих только R – и L – элементы (R – и C – элементы)?
Приведите условия возникновения колебательного переходного процесса.
4 Применение преобразования Лапласа
|
|
|
