 |
4.1 Оригиналы и изображения
|
|
|
|
Пусть f(t) – функция временизадана при t ≥ 0 и равна нулю при  , возрастает не быстрее показательной функции, т. е.
, возрастает не быстрее показательной функции, т. е.  . Здесь M и c0 – некоторые постоянные, положительные и действительные числа. Тогда путем преобразования Лапласа функции f(t) может быть найдена функция F(p) комплексной переменной p. При этом функция f(t) называется оригиналом, а F(p) – изображением. По изображению с помощью обратного преобразования Лапласа может быть найден оригинал. В сокращенной записи соответствие между изображением и оригиналом обозначается, как F(p) = L{f(t)}, f(t) = L-1{F(p)}.
. Здесь M и c0 – некоторые постоянные, положительные и действительные числа. Тогда путем преобразования Лапласа функции f(t) может быть найдена функция F(p) комплексной переменной p. При этом функция f(t) называется оригиналом, а F(p) – изображением. По изображению с помощью обратного преобразования Лапласа может быть найден оригинал. В сокращенной записи соответствие между изображением и оригиналом обозначается, как F(p) = L{f(t)}, f(t) = L-1{F(p)}.
Рассмотрим важное свойство, на основании которого преобразование Лапласа используется при анализе электрических цепей. Пусть 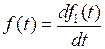 и
и  , тогда
, тогда
F(p) = L{f(t)} = pF1(p) – f1(0) (4. 1)
Пользуясь этим свойством, можно определить изображение производной любого порядка. Например, если  иF1(p) = L{f(t)} тогда
иF1(p) = L{f(t)} тогда

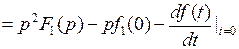 .
.
В приведенных выше выражениях начальные значения функции и ее производных могут определяться при t = 0 или при t = 0 – в зависимости от конкретного применения.
4. 2 Решение дифференциальных уравнений
Здесь рассмотрим применение преобразования Лапласа для решения дифференциального уравнения, которое составлено для классического анализа переходного процесса. Проведем это на примере уравнения (3. 4). Осуществим преобразование Лапласа обеих частей этого уравнения, получим с учетом (4. 1)
 . Правая полученного уравнения – преобразование Лапласа от функции, равной U при t ≥ 0. Из этого уравнения
. Правая полученного уравнения – преобразование Лапласа от функции, равной U при t ≥ 0. Из этого уравнения
 . Тогда оригинал
. Тогда оригинал
 , что совпадает с (3. 5).
, что совпадает с (3. 5).
4. 3 Операторная схема замещения
Составление дифференциального уравнения и определение зависимых начальных условий для схемы, используемой при анализе переходного процесса классическим методом, можно избежать, если от этой схемы перейти по определенным правилам к так называемой операторной схеме замещения. В операторной схеме вместо ЭДС, напряжений и токов используются их изображения по Лапласу. Кроме того, вводится понятие Z – элемента и операторного сопротивления Z(p) этого элемента. Связь между изображением тока I(p) и изображением напряжения U(p) на Z – элементе с операторным сопротивлением Z(p) определяется законом Ома в операторной форме: U(p) = Z(p)I(p).
|
|
|
Замещение L – элемента при переходе к операторной схеме осуществляется исходя из следующего. Поскольку 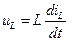 , то на основании (4. 1) UL(p) = LpIL(p) – LiL(0). Величину Z(p) = L(p) принято называть операторным сопротивлением L – элемента. Рис. 4. 1 поясняет указанное замещение. На рис. 4. 1, а показан участок исходной схемы с L – элементом, а на рис. 4. 1 б – соответствующий участок операторной схемы
, то на основании (4. 1) UL(p) = LpIL(p) – LiL(0). Величину Z(p) = L(p) принято называть операторным сопротивлением L – элемента. Рис. 4. 1 поясняет указанное замещение. На рис. 4. 1, а показан участок исходной схемы с L – элементом, а на рис. 4. 1 б – соответствующий участок операторной схемы
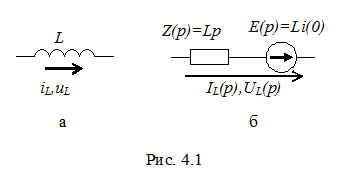 Таким образом, L – элементу на исходной схеме соответствуют два последовательно соединенные элемента: Z – элемент с операторным сопротивлением Z(p) = Lp и источник э. д. с., изображение которой E(p) = Li(0).
Таким образом, L – элементу на исходной схеме соответствуют два последовательно соединенные элемента: Z – элемент с операторным сопротивлением Z(p) = Lp и источник э. д. с., изображение которой E(p) = Li(0).
 Замещение С – элемента при переходе к операторной схеме осуществляется исходя из следующего. Поскольку
Замещение С – элемента при переходе к операторной схеме осуществляется исходя из следующего. Поскольку  , то на основании (4. 1) LC(p) = CpUC(p) – CuC(0), откуда
, то на основании (4. 1) LC(p) = CpUC(p) – CuC(0), откуда  . Величину
. Величину  принято называть операторным сопротивлением C – элемента. Рис. 4. 2 поясняет указанное замещение. На рис. 4. 2 а показан участок исходной схемы с C – элементом, а на рис. 4. 2 б – соответствующий участок операторной схемы.
принято называть операторным сопротивлением C – элемента. Рис. 4. 2 поясняет указанное замещение. На рис. 4. 2 а показан участок исходной схемы с C – элементом, а на рис. 4. 2 б – соответствующий участок операторной схемы.
Таким образом, C – элементу на исходной схеме соответствуют два последовательно соединенные элемента: Z – элемент с операторным сопротивлением  и источник ЭДС, изображение которой
и источник ЭДС, изображение которой  .
.
 Замещение R – элемента при переходе к операторной схеме осуществляется исходя из следующего. Поскольку uR = RiR, то UR(p) = RIR(p). Величину Z(p) = R назовем операторным сопротивлением R – элемента. Рис. 4. 3 поясняет указанное замещение. На рис. 4. 3, а показан участок исходной схемы с R – элементом, а на рис. 4. 3 б – соответствующий участок операторной схемы. Таким образом, R – элементу на исходной схеме соответствует Z – элемент с операторным сопротивлением
Замещение R – элемента при переходе к операторной схеме осуществляется исходя из следующего. Поскольку uR = RiR, то UR(p) = RIR(p). Величину Z(p) = R назовем операторным сопротивлением R – элемента. Рис. 4. 3 поясняет указанное замещение. На рис. 4. 3, а показан участок исходной схемы с R – элементом, а на рис. 4. 3 б – соответствующий участок операторной схемы. Таким образом, R – элементу на исходной схеме соответствует Z – элемент с операторным сопротивлением  .
.
|
|
|
Для операторных схем справедливы законы Кирхгофа в операторной форме. Первый закон Кирхгофа: алгебраическая сумма изображений токов, связанных с узлом, равна нулю. Второй закон Кирхгофа: алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на элементах этого контура.
 Рассмотрим использование метода на примере анализа переходного процесса в схеме, приведенной на рис. 3. 7, при переключении контактов коммутирующего элемента из нижнего положения в верхнее. Операторная схема для этого случая приведена на рис. 4. 4.
Рассмотрим использование метода на примере анализа переходного процесса в схеме, приведенной на рис. 3. 7, при переключении контактов коммутирующего элемента из нижнего положения в верхнее. Операторная схема для этого случая приведена на рис. 4. 4.
По второму закону Кирхгофа можно записать следующие два уравнения:
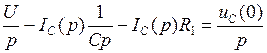 ,
,
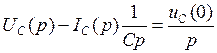 .
.
Тогда из первого уравнения 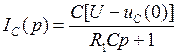 . Подставляя это выражение во второе уравнение получим
. Подставляя это выражение во второе уравнение получим
 .
.
Найдем оригинал
 ,
,
что совпадает с (3. 5).
4. 4 Передаточная функция
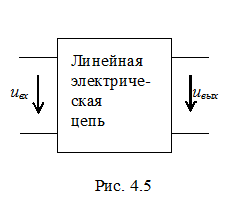 Часто приходится анализировать цепи, обобщенная схема которых представлена на рис. 4. 5 и для которых заданы нулевые независимые начальные условия.
Часто приходится анализировать цепи, обобщенная схема которых представлена на рис. 4. 5 и для которых заданы нулевые независимые начальные условия.
Здесь uвх и uвых – входное и выходное напряжения на некоторых выводах цепи, причем зависимость между ними при – ∞ < t < ∞ описывается уравнением вида (3. 3):
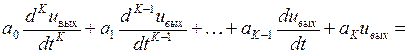
 . (4. 2)
. (4. 2)
Кроме того, uвх = 0 и uвых = 0 при t < 0. Начальные условия для напряжений и их производных задаются при t = 0 – поэтому все они оказываются нулевыми. В общем случае анализ таких цепей заключается в определении выходного напряжения при заданном входном. В частности таким образом может быть проанализирован переходный процесс, связанный со скачкообразным изменением входного напряжения.
Осуществим преобразование Лапласа обеих частей уравнения (4. 2) с учетом (4. 1), получим
а0рKUвых(p) + a1pK–1Uвых(p) +... + aК–1pUвых(p) + aКUвых(p)=
=b0рМUвх(p) + b1pМ–1Uвх(p) +... + bМ–1pUвх(p) + bМUвх(p).
Отсюда
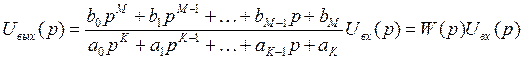 ,
,
где
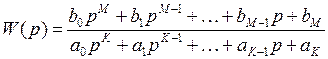 (4. 3)
(4. 3)
|
|
|
называется передаточной функцией цепи. Необходимо отметить, что входными и выходными величинами могут быть не только напряжения на некоторых выводах цепи, но и токи в элементах этой цепи. Более того, входной величиной может быть ток, а выходной – напряжение и наоборот.
Входную величину часто называют входным воздействием или входным сигналом, а выходную – реакцией цепи на некоторое входное воздействие или выходным сигналом.
Как следует из (4. 3), передаточная функция зависит только от параметров элементов цепи. Она может быть найдена, исходя из дифференциального уравнения цепи или из операторной схемы замещения. Если известна передаточная функция цепи, то можно найти выходную величину при заданной входной. Для этого необходимо найти изображение входной величины, например Uвх(p) = L{uвх(t)}, затем определить изображение выходной величины Uвых(р) = W(p)Uвх(р) и ее оригинал
uвых(t) = L-1{Uвых(p)}.
Существует типовая характеристика, по которой можно судить о характере переходных процессов в цепи. Она называется переходной характеристикой цепи. Переходная характеристика h(t) представляет собой реакцию цепи на входное воздействие в виде единичной ступенчатой функции 1(t). По определению 1(t) = 0 при t < 0; 1(t) = 1 при t ≥ 0. Поскольку  , изображение переходной характеристики
, изображение переходной характеристики  , переходная характеристика
, переходная характеристика 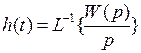 .
.
Для примера, определим передаточную функцию и переходную характеристику цепи, схема которой приведена на рис. 4. 6.
 На основании второго закона Кирхгофа
На основании второго закона Кирхгофа  .
.
Подставив в это уравнение значение тока через C – элемент  , получим линейное дифференциальное уравнение второго порядка относительно uвых:
, получим линейное дифференциальное уравнение второго порядка относительно uвых:
 .
.
Выполним над обеими частями этого уравнения преобразование Лапласа, имея в виду, что все начальные условия задаются при t = 0 – и равны нулю. Получим LCp2Uвых(P) + RCpUвых (p) + Uвых(p) = Uвх(p). Определим из этого выражения Uвых(p): 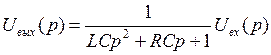 , откуда следует, что
, откуда следует, что
 .
.
Как указывалось выше, выражение для передаточной функции может быть получено путем анализа операторной схемы замещения, которая в данном случае имеет вид, показанный на рис. 4. 7.
|
|
|
 Анализируя эту схему, нетрудно получить, что
Анализируя эту схему, нетрудно получить, что
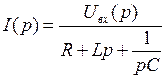 ,
,
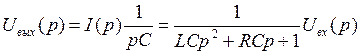 , откуда
, откуда
 ,
,
где  – коэффициент затухания;
– коэффициент затухания; 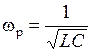 – резонансная частота.
– резонансная частота.
Определим переходную характеристику цепи. Изображение этой характеристики
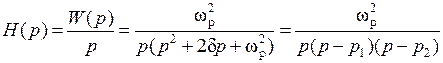 ,
,
где 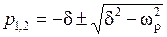 – корни уравнения
– корни уравнения 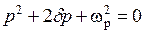 . Используя таблицы преобразования Лапласа нетрудно определить оригинал
. Используя таблицы преобразования Лапласа нетрудно определить оригинал
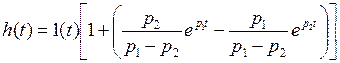 .
.
 При δ > ω р корни p1 и p2 различные и отрицательные, переходная характеристика носит апериодический характер и имеет вид, изображенный на рис. 4. 8.
При δ > ω р корни p1 и p2 различные и отрицательные, переходная характеристика носит апериодический характер и имеет вид, изображенный на рис. 4. 8.
При δ < ω р корни комплексно сопряженные: p1 = –δ + jω 0, p2 = –δ – jω 0, где  – угловая частота собственных колебаний. Переходная характеристика носит колебательный характер:
– угловая частота собственных колебаний. Переходная характеристика носит колебательный характер:
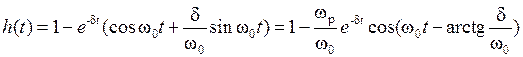 . Графически ее можно представить в виде, приведенном на рис. 4. 9.
. Графически ее можно представить в виде, приведенном на рис. 4. 9.

4. 5 Особенности анализа переходных процессов
Рассмотрим электрическую цепь, изображенную на рис. 4. 10.

Пусть необходимо определить напряжение uR при замыкании коммутирующего элемента. Составим дифференциальное уравнение, описывающее переходный процесс, относительно uR. По второму закону Кирхгофа после замыкания коммутирующего элемента, т. е. для t ³ 0, можно записать иС + иR = u. Продифференцируем обе части уравнения, получим 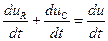 . Имея в виду, что
. Имея в виду, что 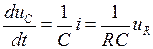 , окончательно
, окончательно
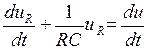 (4. 4)
(4. 4)
Будем считать, что u = U и uC(0) = uC(0 –) = 0. Тогда уравнение (4. 4) примет вид,

а начальное условие uR(0) = U. Нетрудно получить решение этого уравнения в виде 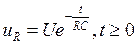 .
.
Теперь найдем решение уравнения (4. 4) с помощью преобразования Лапласа, для чего осуществим это преобразование над обеими частями уравнения, тогда  . Поскольку
. Поскольку  , из приведенного уравнения можно получить
, из приведенного уравнения можно получить 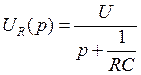 . Выполнив обратное преобразование Лапласа, находим
. Выполнив обратное преобразование Лапласа, находим 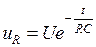 .
.
Определить uR можно путем перехода к операторной схеме замещения. Поскольку uC(0) = 0, эта схема будет иметь вид, показанный на рис. 4. 11.
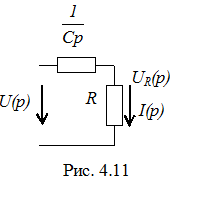 Имея в виду, что u = U,
Имея в виду, что u = U,  , нетрудно получить
, нетрудно получить
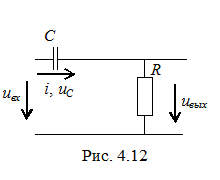
 ,
,  . Далее найдем оригинал
. Далее найдем оригинал 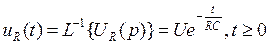 .
.
Рассмотрим далее цепь, схема которой приведена на рис. 4. 12. Здесь uвх = 0 и uвых = 0 при t < 0.
По второму закону Кирхгофа иС + ивых = uвх. Продифференцируем обе части уравнения и имея в виду, что  , нетрудно получить дифференциальное уравнение для этой цепи в виде.
, нетрудно получить дифференциальное уравнение для этой цепи в виде.
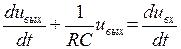 (4. 5)
(4. 5)
За начальные условия при анализе цепи примем значения напряжений при t = 0 –. Кроме того, будем считать, что независимое начальное условие uC(0 –) = 0. Тогда uвых(0 –) = 0 Определим передаточную функцию этой цепи, для этого осуществим преобразование Лапласа обеих частей приведенного уравнения с учетом (4. 1). Получим
|
|
|
 , отсюда
, отсюда  , и передаточная функция цепи
, и передаточная функция цепи 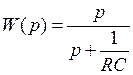 .
.
Передаточная функция может быть найдена путем анализа операторной схемы замещения, которая в данном с учетом нулевых независимых начальных условий будет иметь вид, показанный на рис. 4. 13.

Для этой схемы
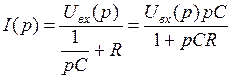 ,
,  , отсюда передаточная функция
, отсюда передаточная функция 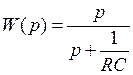 . Используя передаточную функцию, определим uвых при uвх = U1(t). При этом
. Используя передаточную функцию, определим uвых при uвх = U1(t). При этом
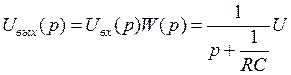 ,
, 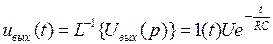 .
.
Изложенное выше позволяет отметить следующие особенности анализа переходных процессов.
При анализе переходного процесса в схеме на рис. 4. 10 с коммутирующим элементом дифференциальное уравнение (4. 4) составлено для t ³ 0, т. е. для интервала времени, на котором отсутствуют скачкообразные изменения напряжений и токов на элементах. Для решения такого уравнения должны быть предварительно определены как независимые, так и зависимые начальные условия при t = 0. Если анализ проводится путем перехода к операторной схеме замещения, показанной на рис. 4. 11, то предварительно должны быть определены только независимые начальные условия при t = 0. Результат анализа в любом случае определен при t ³ 0.
При анализе переходного процесса в схеме на рис. 4. 12 без коммутирующего элемента дифференциальное уравнение (4. 5) составлено для всего интервала времени, на котором определены входные и выходные сигналы, т. е. для – ¥ < t < ¥, который включает моменты скачкообразного изменения напряжений и токов на элементах. Для решения такого уравнения должны быть предварительно определены как независимые, так и зависимые начальные условия при t = 0 –, которые в данном случае равны нулю. Анализ может быть проведен с использованием передаточной функции. Результат анализа определен при – ¥ < t < ¥.
4. 6 Вопросы и задания для самопроверки
Получите изображения по Лапласу для сигнала в виде прямоугольного импульса, синусоидального импульса.
Как на практике осуществляется переход от оригинала к изображению и обратный переход?
Как используется преобразование Лапласа при решении дифференциального уравнения, описывающего переходный процесс?
Что такое операторная схема замещения?
Для каких цепей и как вводится понятие передаточной функции?
Определите передаточные функции цепи, состоящей из последовательно соединенных R – и L – элементов (R – и C – элементов) исходя из дифференциального уравнения.
Выполните предыдущее задание исходя из операторной схемы замещения.
5 ЧАСТОТНЫЙ АНАЛИЗ
5. 1 Представление периодических сигналов рядом Фурье
При разложении в ряд Фурье сигнал, имеющий период T записывается в виде
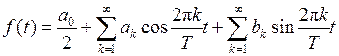 ,
,
где 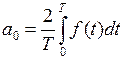 ,
,  ,
,  – коэффициенты ряда. Отметим, что пределы интегрирования в этих формулах могут выбираться в определенной степени произвольно. Необходимо только, чтобы интервал интегрирования был равен T.
– коэффициенты ряда. Отметим, что пределы интегрирования в этих формулах могут выбираться в определенной степени произвольно. Необходимо только, чтобы интервал интегрирования был равен T.
Это разложение может быть представлено по-другому
,  (5. 1)
(5. 1)
где 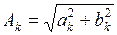 ;
;  . Значение γ k определяется из следующих уравнений:
. Значение γ k определяется из следующих уравнений:  ;
;  . Величина γ k из этих уравнений определяется с точностью до слагаемого 2π n, где n – любое целое число. Обычно используют значения– π < γ k ≤ π. Тогда
. Величина γ k из этих уравнений определяется с точностью до слагаемого 2π n, где n – любое целое число. Обычно используют значения– π < γ k ≤ π. Тогда 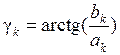 при ak ≥ 0,
при ak ≥ 0, 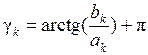 при ak < 0 и bk ≥ 0,
при ak < 0 и bk ≥ 0,  при ak < 0 и bk < 0.
при ak < 0 и bk < 0.
Часто используется комплексная форма ряда Фурье:
 (5. 2)
(5. 2)
где комплексные коэффициенты ряда
,  (5. 3)
(5. 3)
причем  ,
,  ,
,  ,
,  . Здесь k = 1, 2, …. Выражение
. Здесь k = 1, 2, …. Выражение  обозначает главное значение аргумента комплексного числа
обозначает главное значение аргумента комплексного числа  , причем
, причем 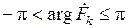 . Решетчатую функцию
. Решетчатую функцию  принято называть комплексным спектром, функцию
принято называть комплексным спектром, функцию  - амплитудным спектром, а функцию
- амплитудным спектром, а функцию 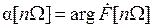 называют фазовым спектром. Заметим, что
называют фазовым спектром. Заметим, что  при
при  ,
,  при
при  и
и  ,
, 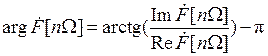 при
при  и
и 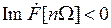 .
.
Определим для примера амплитудный и фазовый спектры периодической последовательности прямоугольных импульсов, параметры которой определены на рис. 5. 1. Нетрудно получить, что

 ,
,
 ,
, 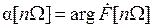 .
.
На рис. 5. 2 показан амплитудный спектр, а на рис. 5. 3 – фазовый спектр при T = 4tи.

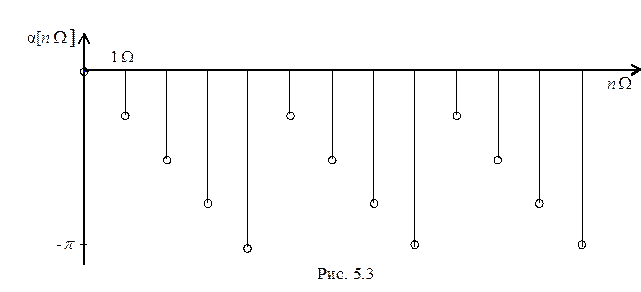
5. 2 Полоса частот, занимаемая периодическим сигналом
Определим квадрат действующего значения периодического сигнала:  . Если сигнал представляет собой ток или напряжение, то эта величина прямо пропорциональна средней за период мощности сигнала. Используя (5. 2), можно получить
. Если сигнал представляет собой ток или напряжение, то эта величина прямо пропорциональна средней за период мощности сигнала. Используя (5. 2), можно получить
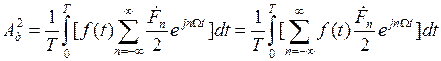 .
.
Меняя местами интегрирование и суммирование, получим
 ,
,
где 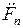 – величина комплексно сопряженная величине
– величина комплексно сопряженная величине  . Имея в виду обозначения, используемые в (5. 1), окончательно
. Имея в виду обозначения, используемые в (5. 1), окончательно
 ,
,
где – действующее k-й составляющей.
Практической шириной полосы частот, занимаемой сигналом, считают полосу Δ, в которой сосредоточена определенная часть мощности сигнала, например, 90%. Δ = ω 2 – ω 1, где ω 1 и ω 2 – нижняя и верхняя частоты полосы. Указанные частоты могут быть выбраны в значительной степени произвольно. Пусть ω 1 = 0, ω 2 = KΩ, тогда Δ = KΩ, а величина K определится с помощью следующего неравенства:
.
При этом определяется такое наименьшее значение K, при котором выполняется это неравенство.
Для примера, определим полосу частот, занимаемую сигналом, изображенным на рис. 5. 1 при T = 4tи. В этом случае K = 3, Δ = 3Ω. Если для этого же сигнала определить полосу частот, в которой сосредоточено 99% мощности, то K = 40, Δ = 40Ω.
5. 3 Частотные характеристики непериодических сигналов
Рассмотрим сначала непериодический сигнал f(t), все ненулевые значения которого сосредоточены на определенном интервале времени T, а за пределами этого интервала сигнал имеет нулевые значения. Такой сигнал может быть получен из периодического сигнала с периодом T при T → ∞ . Например, непериодический сигнал в виде прямоугольного импульса, изображенный на рис. 5. 4 можно получить из периодического сигнала на рис. 5. 1 при T → ∞ .
Используя этот прием, можно определить частотные характеристики непериодических сигналов, исходя из характеристик периодических сигналов. При увеличении периода составляющие амплитудного спектра уменьшаются, а число их на заданном частотном интервале увеличивается. Для периодического сигнала, подставив (5. 3) в (5. 2) получим
.
Учитывая, что и что пределы интегрирования можно выбирать в определенной степени произвольно (необходимо только, чтобы интервал интегрирования был равен T)
.
При T → ∞ суммирование может быть заменено интегрированием. При этом величина nΩ заменяется на непрерывную частоту ω, а Ω заменяется на dω. Тогда последнее выражение можно записать в виде
(5. 4)
Внутренний интеграл в данном выражении пропорционален комплексному коэффициенту (5. 2) при T → ∞ . По его значениям при различных частотах ω можно судить о соотношении составляющих комплексного спектра. Обозначим этот интеграл
(5. 5)
Эта формула представляет собой преобразование Фурье сигнала f(t). При частотном анализе сигнала величину F(jω ) принято называть спектральной плотностью сигнала. Как известно, преобразование Фурье (5. 5) существует, если сигнал f(t) удовлетворяет условию абсолютной интегрируемости. В общем случае спектральная плотность является комплексной величиной. Ее модуль называется амплитудной характеристикой сигнала F(ω ) = |F(jω )|, а аргумент a(ω ) = argF(jω ) – фазовой характеристикой сигнала.
Обратное преобразование Фурье позволяет по спектральной плотности определить сигнал:
(5. 6)
Это выражение получается из (5. 4), если заменить внутренний интеграл в соответствии с (5. 5).
В общем случае спектральная плотность сигнала – величина комплексная и ее можно представить в виде
F(jω ) = F1(ω ) + jF2(ω ) (5. 7)
где на основании (5. 5),
, .
Имея в виду, что F1(ω ) – четная, а F2(ω ) – нечетная функция частоты, (5. 6) можно записать в виде
. (5. 8)
В ряде случаев вычисления по формулам (5. 7) и (5. 8) оказываются проще, чем по формулам (5. 5) и (5. 6).
В качестве примера определим спектральную плотность сигнала, изображенного на рисунке 5. 4. Используя (5. 5), получим
.
Несложные преобразования последнего выражения позволяют получить
. (5. 9)
Тогда
, .
Заметим, что правая часть равенства (5. 9) легко получается с помощью (5. 7). Графически зависимости F(ω ) и a(w) показаны на рис. 5. 5 и 5. 6 соответственно.
5. 4 Полоса частот, занимаемая непериодическим сигналом
Определим величину. Если сигнал представляет собой ток или напряжение, то эта величина прямо пропорциональна энергии сигнала. Используя (5. 6) и меняя порядок интегрирования, можно получить
.
Имея в виду, что, где - величина комплексно сопряженная F(jω ), будем иметь
.
Практической шириной полосы частот, занимаемой непериодическим сигналом, считают полосу Δ, в которой сосредоточена определенная часть энергии сигнала, например, 90%. Δ = ω 2 – ω 1, где ω 1 и ω 2 – нижняя и верхняя частоты полосы. Указанные частоты могут быть выбраны в значительной степени произвольно. Пусть ω 1 = 0, тогдаΔ = ω 2, а величина ω 2 определится с помощью следующего равенства:
.
При этом определяется такое значение ω 2, при котором выполняется это равенство.
Для примера, определим полосу частот, занимаемую сигналом, изображенным на рис. 5. 4. В этом случае. Если для этого же сигнала определить полосу частот, в которой сосредоточено 99% энергии, то.
5. 5 Комплексная передаточная функция
Рассмотрим сначала важное свойство, на основании которого преобразование Фурье используется при анализе электрических цепей. Пусть и F1(jω ) – преобразование Фурье сигнала f1(t), тогда
F(jω ) = (jω )kF1(jω ) (5. 10)
Как уже указывалось выше, часто приходится анализировать цепи, обобщенная схема которых представлена на рис. 5. 7.
Здесь uвх и uвых – входное и выходное напряжения на некоторых выводах цепи, которые удовлетворяют условию абсолютной интегрируемости, а зависимость между ними описывается уравнением вида (3. 3):
. (5. 11)
Осуществим преобразование Фурье обеих частей уравнения (5. 11), получим
a0(jω )KUвых(jω ) + a1(jω )K–1Uвых(jω ) +... + aК–1jω Uвых(jω ) + aКUвых(jω )=
=b0(jω )МUвх(jω ) + b1(jω )М–1Uвх(jω ) +... + bМ–1jω Uвх(jω ) + bМUвх(jω ).
Отсюда
.
Обозначим
, (5. 12)
Тогда Uвых(jω ) = W(jω )Uвх(jω ). W(jω ) называется комплексной передаточной функцией цепи.
Как следует из (5. 12), передаточная функция зависит только от параметров элементов цепи. Она может быть найдена, исходя из дифференциального уравнения цепи. Если известна передаточная функция цепи, то можно найти выходную величину при заданной входной. Для этого необходимо найти преобразование Фурье входного сигнала, например Uвх(jω ), затем определить преобразование Фурье выходного сигнала Uвых(jω ) = W(jω )Uвх(jω ), а затем определить выходной сигнал uвых(t), выполнив обратное преобразование Фурье над Uвых(jω ).
Если для входного периодического сигнала uвх по формуле (5. 3) определен комплексный спектр Uвх[nΩ ]. Тогда нетрудно показать, что при известной комплексной передаточной функции цепи W(jω ) комплексный спектр выходного периодического сигнала и по формуле (5. 2) можно определить выходной периодический сигнал uвых.
5. 6 Комплексная схема замещения
Комплексная передаточная функция может быть найдена с использованием так называемой комплексной схемы замещения. В такой схеме вместо ЭДС, напряжений и токов используются их преобразования Фурье, которые будем называть комплексными ЭДС, напряжениями и токами. Кроме того, вводится понятие Z – элемента и комплексного сопротивления Z(jω ) этого элемента. Связь между комплексным током I(jω ) и напряжением U(jω ) на Z – элементе с операторным сопротивлением Z(jω ) определяется законом Ома в комплексной форме: U(jω ) = Z(jω )I(jω ).
Замещение L – элемента при переходе к комплексной схеме поясняется рис. 5. 8. Поскольку, то на основании (5. 10). Величину Z(jω ) = jω I принято называть операторным сопротивлением L – элемента. На рис. 5. 8 а показан участок исходной схемы с L – элементом, а на рис. 5. 8 б – соответствующий участок комплексной схемы.
Замещение С-элемента при переходе к комплексной схеме поясняется рис. 5. 9. Поскольку, то на основании (5. 10) IC(jω ) = jω CUC(jω ), откуда. Величину принято называть комплексным сопротивлением C-элемента. На рис. 5. 9 а показан участок исходной схемы с C-элементом, а на рис. 5. 9 б – соответствующий участок комплексной схемы.
Замещение R-элемента при переходе к комплексной схеме поясняет рис. 5. 10. Поскольку uR = RiR, то UR(jω ) = RIR(jω ). Величину Z(jω ) = R назовем комплексным сопротивлением R – элемента. На рис. 5. 10 а показан участок исходной схемы с R – элементом, а на рис. 5. 10 б – соответствующий участок комплексной схемы.
Для комплексных схем справедливы законы Кирхгофа в комплексной форме. Первый закон Кирхгофа: алгебраическая сумма комплексных токов, связанных с узлом, равна нулю. Второй закон Кирхгофа: алгебраическая сумма комплексных ЭДС, действующих в контуре, равна алгебраической сумме комплексных напряжений на элементах этого контура. Рассмотрим схему цепи на рис. 5. 11.
По второму закону Кирхгофа uC + uвых = ивх. Продифференцируем обе части уравнения и имея в виду, что, нетрудно получить дифференциальное уравнение для этой цепи в виде
.
Осуществим преобразование Фурье обеих частей этого уравнения, получим, отсюда, и комплексная передаточная функция цепи
.
Определим теперь комплексную передаточную функцию путем перехода к комплексной схеме замещения, показанной на рис. 5. 12.
Для этой схемы
, , тогда комплексная передаточная функция. Используя эту комплексную передаточную функцию, определим реакцию цепи при воздействии на ее вход импульса, изображенного на рис. 5. 13.
Найдем сначала спектральную плотность этого сигнала, воспользовавшись (5. 9), тогда
.
Представим полученную выше комплексную передаточную функцию в виде
.
Спектральная плотность выходного сигнала
. Вос
пользовавшись обратным преобразованием Фурье (5. 6) или (5. 8), можно определить выходной сигнал. Графически этот сигнал показан на рис. 5. 14 при tu = 5RC.
По реакции цепи при воздействии на ее вход импульса, изображенного на рис. 5. 13. удобно исследовать переходный процесс в цепи. Отметим также, что комплексную передаточную функцию вида (5. 11) формально можно получить, подставив в (4. 3) вместо p выражение jw.
5. 7 Амплитудно-частотная и фазо-частотная характеристики
Исходя из комплексной передаточной функции W(jw) вида (5. 11) можно получить две важные частотные характеристики цепи: амплитудно-частотную характеристику W(ω ) = |W(jω )| и фазо-частотную характеристику φ (ω ) = argW(jω ). С помощью этих характеристик удобно анализировать прохождение синусоидальных сигналов через электрическую цепь. Пусть входной синусоидальный сигнал имеет частоту w1 комплексную амплитуду, а выходной – комплексную амплитуду. Здесь Um вх и Um вых – амплитуды входного и выходного сигналов; gвх иgвых – начальные фазы входного и выходного сигналов. Нетрудно показать, что, тогда
, откуда следует, что Uт вых = W(ω 1)Um вх, γ вых = γ вх + φ (ω ). Таким образом, для определения амплитуды синусоидального сигнала на выходе цепи необходимо амплитуду входного синусоидального сигнала умножить на значение амплитудно-частотной характеристики цепи при частоте этого сигнала. Для нахождения начальной фазы выходного синусоидального сигнала следует к начальной фазе вхо
|
|
|


