 |
переходныЕ процессЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
|
|
|
|
, , , .
Комплексы напряжений участков:
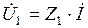 ,
,  ,
,  ,
,  .
.
Комплекс напряжения на входе:
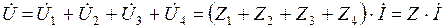 .
.
 При последовательном соединении комплекс полного эквивалентного сопротивления цепи равен сумме комплексов полных сопротивлений ее последовательных участков. Формулами можно пользоваться для расчетатока в цепи по заданному напряжению или для определения напряжения на входе двухполюсника по заданному току. В том и другом случаях необходимо задаться произвольной начальной фазой напряжения или тока.
При последовательном соединении комплекс полного эквивалентного сопротивления цепи равен сумме комплексов полных сопротивлений ее последовательных участков. Формулами можно пользоваться для расчетатока в цепи по заданному напряжению или для определения напряжения на входе двухполюсника по заданному току. В том и другом случаях необходимо задаться произвольной начальной фазой напряжения или тока.
Для цепи с несколькими участками обычно строят топографическую векторную диаграмму напряжений, каждая точка которой соответствует определенной точке электрической цепи. Чтобы осуществить соответствие точек диаграммы и цепи, построение векторов топографической векторной диаграммы ведут в той же последовательности, в какой обходят электрическую цепь. Обычно направление обхода выбирают противоположным положительному направлению тока в цепи.
В последовательной цепи во всех ее участках имеется один и тот же ток I, поэтомуза исходный вектор удобно выбрать вектор тока и относительноего ориентировать все векторы напряжений участков.
При построении топографической векторной диаграммы схемы рис. 2. 9, вектор тока направляем горизонтально и обход цепи против направления тока начинаем с точки а, потенциал которой принимаем за исходный. При переходе к точке b потенциал увеличится на величину падения напряжения в сопротивлении x1. Вектор этого напряжения 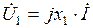 опережает по фазе вектор тока на угол сдвига фаз
опережает по фазе вектор тока на угол сдвига фаз  . Потенциал точки с будет выше потенциала точки b на величину напряжения на втором участке, вектор которого
. Потенциал точки с будет выше потенциала точки b на величину напряжения на втором участке, вектор которого 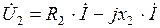 имеет активную и емкостную составляющие. Векторы этих напряжений отложены на диаграмме в той же последовательности, в какой совершается обход цепи. Аналогично построены векторы напряжений и других участков цепи. Вектор результирующего напряжения U расположен между точками e и a. По топографической векторной диаграмме легко определить вектор напряжения между двумя произвольными точками цепи.
имеет активную и емкостную составляющие. Векторы этих напряжений отложены на диаграмме в той же последовательности, в какой совершается обход цепи. Аналогично построены векторы напряжений и других участков цепи. Вектор результирующего напряжения U расположен между точками e и a. По топографической векторной диаграмме легко определить вектор напряжения между двумя произвольными точками цепи.
|
|
|
2. 3. 9. Цепь синусоидального тока с параллельно соединенными приемниками
 Рассмотрим схему цепи рис. 2. 10, состоящую из двух параллельных ветвей, параметры которых R1, L1, R2 и C2 заданы. Пусть напряжение U и частота f источника также известны. Необходимо определить токи, мощности цепи и ее эквивалентное сопротивление относительно входных зажимов.
Рассмотрим схему цепи рис. 2. 10, состоящую из двух параллельных ветвей, параметры которых R1, L1, R2 и C2 заданы. Пусть напряжение U и частота f источника также известны. Необходимо определить токи, мощности цепи и ее эквивалентное сопротивление относительно входных зажимов.  Расчет можно начать с выбора начальной фазы общего напряжения, для чего вектор напряжения удобно направить по одной из осей + 1 или + j.
Расчет можно начать с выбора начальной фазы общего напряжения, для чего вектор напряжения удобно направить по одной из осей + 1 или + j.
Примем  , что соответствует направлению вектора
, что соответствует направлению вектора  по оси + 1. Заданные параметры ветвей позволяют записать их комплексы полных сопротивлений:
по оси + 1. Заданные параметры ветвей позволяют записать их комплексы полных сопротивлений:
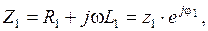
.
Зная комплексные значения  ,
,  ,
, 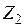 можно найти токи ветвей, пользуясь законом Ома в комплексной форме:
можно найти токи ветвей, пользуясь законом Ома в комплексной форме:  и
и  .
.
Общий ток неразветвленной части цепи определяют по первому закону Кирхгофа: 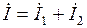 .
.
Составим баланс мощности цепи, по которому комплекс полной мощности источника должен быть равен сумме комплексов полных мощностей ее отдельных ветвей:
 .
.
Мощности ветвей могут быть подсчитаны и по другим формулам:
 ,
,
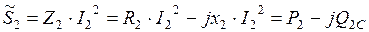 .
.
Суммарная мощность ветвей 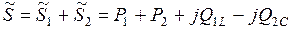 должна быть равна мощности, подсчитанной по формуле
должна быть равна мощности, подсчитанной по формуле  .
.
Для определения комплекса полного эквивалентного сопротивления Z схемы в уравнение полного тока вместо токов подставим их значения, выраженные через напряжение  и сопротивления
и сопротивления 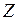 ,
,  и
и 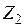 :
:
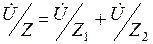 .
.
Отсюда  .
.
Если имеется п параллельных ветвей, то можно записать более общую формулу для определения эквивалентной проводимости:
|
|
|
 .
.
В частности, можно получить простую формулу эквивалентного сопротивления двух параллельных ветвей:
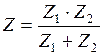 .
.
Построим векторную диаграмму токов заданной цепи (рис. 2. 10). За исходный возьмем вектор напряжения, общий для всех ветвей. Направим этот вектор по оси + 1 и отложим по отношению к нему векторы токов İ 1 и İ 2 ветвей. Вектор тока İ 1 отстает по фазе от вектора напряжения на угол  , а вектор тока İ 2 опережает по фазе вектор напряжения на угол
, а вектор тока İ 2 опережает по фазе вектор напряжения на угол 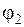 . Вектор тока İ неразветвленного участка, равный геометрической сумме векторов токов ветвей, опережает по фазе вектор напряжения на угол
. Вектор тока İ неразветвленного участка, равный геометрической сумме векторов токов ветвей, опережает по фазе вектор напряжения на угол  .
.
В соответствии с получившейся векторной диаграммой исходная схема может быть заменена емкостным двухполюсником, и мнимая часть комплекса полного эквивалентного сопротивления цепи должна быть отрицательной.
2. 3. 10. Активные и реактивные составляющие проводимости и тока
В цепях синусоидального тока величину, обратную комплексу полного сопротивления Z, называют комплексом полной проводимости и обозначают буквой 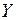 :
:  .
.
Как и всякое комплексное число, комплекс проводимости имеет действительную часть, которую обозначают буквой g и называют активной проводимостью, и мнимую часть, обозначаемую буквой b и называемую реактивной проводимостью. Если цепь активно-индуктивная, то ее комплекс сопротивления Z = R + jxL и комплекс проводимости
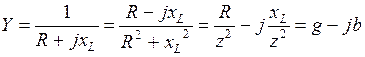 ,
,
где активная проводимость  а реактивная индуктивная проводимость
а реактивная индуктивная проводимость  .
.
Если цепь активно-емкостная, то ее комплекс сопротивления Z = R + jxC и комплекс проводимости
 .
.
Активная проводимость g активно-емкостной цепи определяется той же формулой, что и активная проводимость активно-индуктивной цепи. Реактивная емкостная проводимость 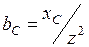 .
.
Мнимая часть комплекса проводимости положительна для емкостной цепи и отрицательна для индуктивной цепи.
При использовании векторных диаграмм для анализа явлений в цепях синусоидального тока пользуются также разложением вектора тока на его активную Ia и реактивную Ip составляющие. Это разложение можно провести графически или аналитически.
|
|
|
При аналитическом способе разложения ток какой-либо ветви представляют произведением комплексных значений напряжения и проводимости:
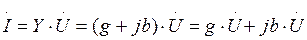 .
.
Величину 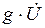 называют активной, величину
называют активной, величину  – реактивной составляющей тока.
– реактивной составляющей тока.
Комплекс активной составляющей тока для индуктивной и емкостной цепей выражается формулой одного и того же вида:
 .
.
Комплекс реактивной составляющей тока определяется следующими формулами:
для индуктивной цепи 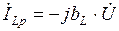 ,
,
для емкостной цепи  .
.
Пользуясь активными и реактивными составляющими проводимости и тока, удобно проводить анализ режимов разветвленной цепи. В качестве примера вернемся к рассмотрению цепи, состоящей из двух параллельных ветвей (см. рис. 2. 10).
Комплекс полной эквивалентной проводимости этой цепи
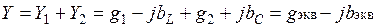 .
.
Если реактивная проводимость индуктивной ветви больше реактивной проводимости емкостной ветви (bL > bC), то Y = gэкв – jbэкв и цепь является активно-индуктивным двухполюсником. Ток неразветвленного участка такой цепи, равный току источника питания, отстает по фазе от напряжения источника. При (bL > bC), цепь представляет собой активно-емкостный двухполюсник.
В параллельной цепи с индуктивными и емкостными приемниками (см. рис. 2. 10) возможно явление, когда общий ток цепи (ток неразветвленного участка) и напряжение на входе цепи совпадают по фазе. Это явление называют резонансом тока.
Реактивные составляющие токов индуктивной и емкостной цепей при резонансе токов равны по величине и противоположны по фазе. Следовательно, при резонансе токов любой параллельной цепи ее реактивный индуктивный ток ILp и реактивный емкостный ток ICp взаимно компенсируются. Цепь представляет собой активный двухполюсник, эквивалентная проводимость которого равна сумме активных проводимостей ветвей: Y = g1 + g2 = gэкв. Цепь имеет только активные составляющие тока I = Ia1 + Ia2 и потребляет только активную энергию. Цепь при резонансе токов не потребляет от источника реактивной энергии. В ней имеет место взаимный обмен энергиями между электрическим и магнитным полями. Источник питания лишь компенсирует потерю энергии в активных сопротивлениях ветвей.
|
|
|
2. 3. 11. Повышение коэффициента мощности в цепях синусоидального тока
Большинство современных потребителей электрической энергии синусоидального тока представляют собой индуктивные нагрузки, токи которых отстают по фазе от напряжений источника питания. Активная мощность таких потребителей при заданных значениях тока и напряжения зависит еще от 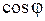 .
.
Если для потребителя задаются его напряжение U и активная мощность Р, то с изменением 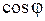 изменяется и ток потребителя. С уменьшением
изменяется и ток потребителя. С уменьшением 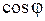 потребителя его ток возрастает:
потребителя его ток возрастает:
 .
.
Генераторы, питающие потребители, рассчитываютна определенную номинальную мощность Sн = Uн ∙ Uн; при заданном напряжении Uн они могут быть нагружены током, не превышающим номинальное значение. Поэтому увеличение тока потребителя вследствие снижения его 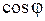 не должно превышать определенных пределов. Чтобы ток генератора не был выше номинального при снижении
не должно превышать определенных пределов. Чтобы ток генератора не был выше номинального при снижении 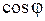 потребителя, необходимо снижать его активную мощность. В этом случае генератор будет полностью нагружен по току и недогружен по активной мощности.
потребителя, необходимо снижать его активную мощность. В этом случае генератор будет полностью нагружен по току и недогружен по активной мощности.
Для сохранения неизменной активной мощности потребителя при снижении 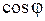 можно было установить генератор на большую номинальную мощность с тем, чтобы увеличение тока вследствие снижения
можно было установить генератор на большую номинальную мощность с тем, чтобы увеличение тока вследствие снижения 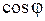 не превышало его номинального значения. В этом случае активная мощность
не превышало его номинального значения. В этом случае активная мощность  , которой будет нагружен генератор, составляет только часть номинальной мощности Sн. Например, при снижении
, которой будет нагружен генератор, составляет только часть номинальной мощности Sн. Например, при снижении 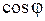 от 1 до 0, 5 нагрузка генератора составляет только 50% от его номинальной мощности. Таким образом,
от 1 до 0, 5 нагрузка генератора составляет только 50% от его номинальной мощности. Таким образом, 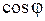 характеризует, как используется номинальная мощность источника, и поэтому его называют коэффициентом мощности.
характеризует, как используется номинальная мощность источника, и поэтому его называют коэффициентом мощности.
Но работа источника питания в целом характеризуется КПД его установки, состоящим из КПД генератора и первичного двигателя. Работа первичного двигателя определяется в основном активной мощностью генератора. Поэтому недогрузка генератора активной мощностью влечет за собой недогрузку и снижение КПД первичного двигателя и всей энергетической установки. Себестоимость электроэнергии от этого повышается. Работа потребителя с малым коэффициентом мощности, кроме ухудшения условий экономического использования источника питания, приводит к увеличению мощности потерь в линии передачи электрической энергии от источника к потребителю. Если сопротивление проводов этой линии r, то мощность потерь в ней  . Мощность потерь, как видно из этого выражения, тем больше, чем ниже
. Мощность потерь, как видно из этого выражения, тем больше, чем ниже 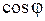 установки. Следовательно, чем ниже
установки. Следовательно, чем ниже 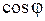 потребителя, тем дороже будет обходиться передача к нему электроэнергии.
потребителя, тем дороже будет обходиться передача к нему электроэнергии.
|
|
|
Чтобы повысить экономичность энергетических установок, принимают меры к повышению коэффициента мощности потребителей. Идея повышения 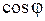 заключается в следующем. Общий ток индуктивного потребителя рассматривают состоящим из активной и реактивной составляющих. Активная мощность потребителя при данном напряжении определяется активной составляющей тока P = U∙ Ia, поэтому при заданном значении активной мощности активная составляющая тока должна оставаться неизменной. Снизить ток потребителя в этом случае можно только за счет уменьшения реактивного тока индуктивного потребителя. Последнее можно осуществить только путем параллельного подключения к нагрузке какого-либо приемника с емкостным током. Таким приемником может быть или синхронный компенсатор, или батарея специальных (косинусных) конденсаторов.
заключается в следующем. Общий ток индуктивного потребителя рассматривают состоящим из активной и реактивной составляющих. Активная мощность потребителя при данном напряжении определяется активной составляющей тока P = U∙ Ia, поэтому при заданном значении активной мощности активная составляющая тока должна оставаться неизменной. Снизить ток потребителя в этом случае можно только за счет уменьшения реактивного тока индуктивного потребителя. Последнее можно осуществить только путем параллельного подключения к нагрузке какого-либо приемника с емкостным током. Таким приемником может быть или синхронный компенсатор, или батарея специальных (косинусных) конденсаторов.
2. 4. Трехфазные электрические цепи
2. 4. 1. Основные понятия. Элементы трехфазных цепей.
Трехфазные цепи представляют собой частный случай многофазных систем переменного тока. Многофазными системами называется совокупность электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой и индуктированные в одном источнике энергии. Каждую из однофазных цепей, входящую в многофазную систему, принято называть фазой(в электротехнике термин «фаза» имеет два значения: понятие, характеризующую стадию периодического процесса, и наименование однофазных цепей, образующих многофазную систему). Цепи в зависимости от числа фаз называются двухфазными, трехфазными, шестифазными и т. п.
Наибольшее распространение в современной электроэнергетике получили трехфазные цепи. Это объясняется рядом их преимуществ, как перед другими многофазными цепями, так и перед однофазными цепями переменного тока. Среди этих преимуществ можно отметить:
экономичность производства и передачи энергии по сравнению с однофазными цепями;
возможность сравнительно простого получения вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя – одного из самых распространенных двигателей переменного тока; возможность получения в одной установке двух эксплуатационных напряжений фазного и линейного.
Трехфазная цепь состоит из трех основных частей или элементов: трехфазного генератора, в котором механическая энергия преобразуется в электрическую энергию с трехфазной системой ЭДС, линии передачи со всем необходимым оборудованием, приемников (потребителей), которые могут быть как трехфазными (например, электродвигатели), так и однофазными (например, лампы накаливания).
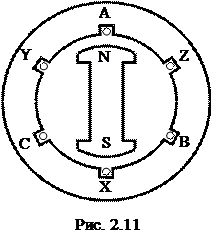 Трехфазный генератор представляет собой синхронную машину двух типов: турбогенератор или гидрогенератор (схематическое изображение модели трехфазного генератора дано на рис. 2. 11). На статоре генератора размещается обмотка, состоящая из трех частей или, как их принято называть, фаз. Обмотки фаз располагаются на статоре таким образом, чтобы их магнитные оси были сдвинуты в пространстве относительно друг друга на угол радиан. Начала обмоток обозначаются буквами A, B, C, а концы – X, Y, Z.
Трехфазный генератор представляет собой синхронную машину двух типов: турбогенератор или гидрогенератор (схематическое изображение модели трехфазного генератора дано на рис. 2. 11). На статоре генератора размещается обмотка, состоящая из трех частей или, как их принято называть, фаз. Обмотки фаз располагаются на статоре таким образом, чтобы их магнитные оси были сдвинуты в пространстве относительно друг друга на угол радиан. Начала обмоток обозначаются буквами A, B, C, а концы – X, Y, Z.
ЭДС в неподвижных витках обмотки статора индуктируются в результате пересечения этих витков магнитным полем, возбуждаемым током обмотки вращающегося ротора (на рис. 2. 11 ротор с обмоткой условно изображен в виде постоянного магнита с полюсами N и S). Расположенная на роторе обмотка возбуждения питается от источника постоянного напряжения (возбудителя). При вращении ротора с равномерной скоростью в обмотках фаз статора индуктируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты, но отличающиеся друг от друга по фазе вследствие их пространственного смещения.
На схемах обмотку (или фазу) источника питания изображают, как показано на рис. 2. 12. За условное положительное направление ЭДС в каждой фазе принимают направление от конца к началу. Обычно индуктированные в катушках ЭДС имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на один и тот же угол  . Такая система ЭДС называется симметричной.
. Такая система ЭДС называется симметричной.

2. 4. 2. Способы изображения симметричной трехфазной системы ЭДС
Симметричная трехфазная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного.
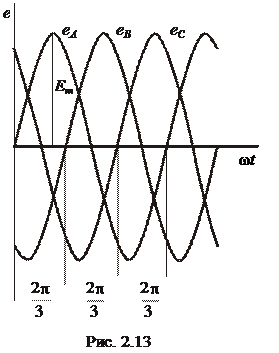 Графики изменения ЭДС симметричной системы показаны на рис. 2. 13. Важно обратить внимание на то, что для симметричной трехфазной системы ЭДС справедливо равенство: eA + eB + eC = 0. Если ЭДС какой-либо отдельной фазы трехфазной обмотки, например фазы A, принять за исходную и считать ее начальную фазу равной нулю, то выражения для мгновенных значений ЭДС можно записать в следующем виде:
Графики изменения ЭДС симметричной системы показаны на рис. 2. 13. Важно обратить внимание на то, что для симметричной трехфазной системы ЭДС справедливо равенство: eA + eB + eC = 0. Если ЭДС какой-либо отдельной фазы трехфазной обмотки, например фазы A, принять за исходную и считать ее начальную фазу равной нулю, то выражения для мгновенных значений ЭДС можно записать в следующем виде:
 ,
,
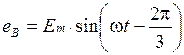 ,
,
 .
.
Соответственно для комплексных значений ЭДС получим уравнения:
 ,
,  ,
, 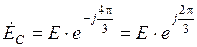 .
.
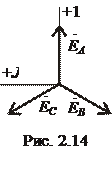 Векторная диаграмма симметричной трехфазной системы ЭДС показана на рис. 2. 14. (Следует обратить внимание на то, что при рассмотрении трехфазных цепей комплексную плоскость обычно поворачивают на угол
Векторная диаграмма симметричной трехфазной системы ЭДС показана на рис. 2. 14. (Следует обратить внимание на то, что при рассмотрении трехфазных цепей комплексную плоскость обычно поворачивают на угол  против часовой стрелки. ) Из векторных диаграмм рис. 2. 14 следует, что для симметричной трехфазной системы геометрическая сумма векторов ЭДС всех фаз равна нулю:
против часовой стрелки. ) Из векторных диаграмм рис. 2. 14 следует, что для симметричной трехфазной системы геометрическая сумма векторов ЭДС всех фаз равна нулю:  . Систему ЭДС, в которой ЭДС фазы В отстает по фазе от ЭДС фазы А, а ЭДС фазы С по фазе – от ЭДС, фазы В, называют системой прямой последовательности. Если изменить направление вращения ротора генератора, то последовательность фаз изменится и будет она называться обратной.
. Систему ЭДС, в которой ЭДС фазы В отстает по фазе от ЭДС фазы А, а ЭДС фазы С по фазе – от ЭДС, фазы В, называют системой прямой последовательности. Если изменить направление вращения ротора генератора, то последовательность фаз изменится и будет она называться обратной.
Последовательность фаз определяет направление вращения трехфазных двигателей, ее нужно учитывать также при включении трехфазных генераторов на параллельную работу. Для определения последовательности фаз имеются специальные приборы – фазоуказатели.
Поскольку на практике применяется прямая последовательность фаз, в данной главе будут рассматриваться трехфазные цепи только с прямой последовательностью фаз.
2. 4. 3 Способы соединения трехфазного источника питания
Если фазы обмотки электрически не соединены между собой, то они образуют несвязанную трехфазную систему цепей. В этом случае каждая из фаз должна соединяться со своим приемником двумя проводами (рис. 2. 15). Несвязанные цепи не получили применения вследствие их неэкономичности, вызванной большим числом проводов, соединяющих источник питания и приемники.
Так, например, в трехфазной несвязанной системе таких проводов будет шесть. Более совершенными и экономичными являются связанные цепи, в которых фазы обмотки электрически соединены между собой. В дальнейшем будут рассматриваться связанные трехфазные цепи с соединением фаз обмоток звездой или треугольником, разработанные и внедренные в практику М. О. Доливо-Добровольским в начале 90-х годов прошлого века.

При соединении фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 2. 16). Начала фаз выводят к зажимам, обозначаемым соответственно A, B и C. К ним подключают провода, с помощью которых источник питания соединяется с приемником. Эти провода называются линейными, а трехфазная цепь – трехпроводной. В случае, когда нейтральная точка N источника питания соединена с нейтральной точкой n приемника (см. рис. 2. 19), трехфазная цепь будет четырехпроводной. Провод, соединяющий нейтральные точки N и n, называется нейтральным.
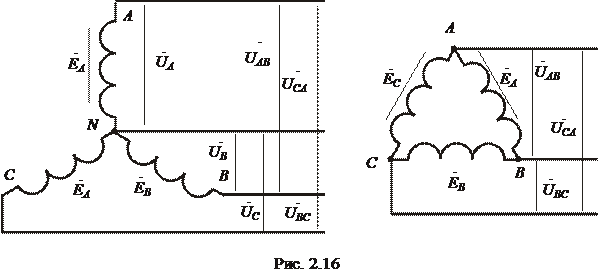
При соединении фаз источника питания треугольником объединяются (соединяются) в одну точку соответствующие начала и концы фаз: X-B, Y-C, Z-A (см. рис. 2. 16). При этом фазы источника оказываются соединенными последовательно. Соединение фаз источника в замкнутый треугольник не равносильно их короткому замыканию (как это имело бы место при подобном соединении фаз источников синусоидального тока), так как при симметричной системе ЭДС сумма их мгновенных значений eA + eB + eC = 0. Поэтому при холостом ходе ток в фазах источника не возникает. Однако, как будет показано далее, на практике фазы трехфазных генераторов предпочитают соединять звездой.
Напряжения между началом и концом (или между выводами) каждой фазы источника uA, uB, uC называют фазными, а между одноименными выводами разных фаз – линейными (uAB, uBC, uCA) (см. рис. 2. 16).
 На практике обычно имеют дело не с отдельными источниками, а с несколькими, соединенными параллельно. В этом случае можно пренебречь внутренними сопротивлениями фаз источника, считать фазные напряжения uA, uB, uC численно равными фазным ЭДС и изображать их симметричной системой векторов (рис. 2. 17). Следует отметить, что система фазных и линейных напряжений источника симметрична вследствие конструктивных особенностей трехфазного генератора.
На практике обычно имеют дело не с отдельными источниками, а с несколькими, соединенными параллельно. В этом случае можно пренебречь внутренними сопротивлениями фаз источника, считать фазные напряжения uA, uB, uC численно равными фазным ЭДС и изображать их симметричной системой векторов (рис. 2. 17). Следует отметить, что система фазных и линейных напряжений источника симметрична вследствие конструктивных особенностей трехфазного генератора.
За условные положительные направления фазных напряжений принимают направление от начала к концу фаз обмоток, а линейных напряжений – от начала одной фазы к началу другой (см. рис. 2. 16). В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений (см. рис. 2. 16) можно записать уравнения по второму закону Кирхгофа и построить по ним векторную диаграмму:
uAB = uA – uB, uBC = uB – uC, uCA = uC – uA.
Комплексные значения линейных напряжений связаны с комплексными значениями фазных напряжений, следующими уравнениями:
 ,
,  ,
, 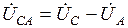 .
.
Отметим, что уравнения позволяют определить линейные напряжения по известным фазным напряжениям. В соответствии с этими уравнениями на рис. 2. 17 построена топографическая (потенциальная) диаграмма фазных и линейных напряжений источника при соединении его фаз звездой.
Из диаграммы видно, что для симметричной системы напряжений линейные напряжения представляют тремя векторами, сдвинутыми по фазе относительно друг друга на угол  ; кроме того, векторы линейных напряжений
; кроме того, векторы линейных напряжений  ,
, 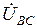 ,
,  опережают по фазе соответственно векторы фазных напряжений
опережают по фазе соответственно векторы фазных напряжений 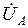 ,
,  и
и  на угол
на угол 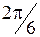 .
.
Следует различать направление стрелок на схеме, указывающих условное положительное направлёние линейных напряжений и направление векторов на векторной диаграмме. Так, очевидно, вектор  должен быть направлен к точке А.
должен быть направлен к точке А.
Величина каждого из векторов линейных напряжений в  раз больше величины вектора фазного напряжения:
раз больше величины вектора фазного напряжения:
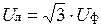 .
.
Следует обратить внимание на важное свойство системы линейных напряжений: независимо от характера нагрузки сумма их мгновенных значений или векторов всегда равна нулю.
Предусмотренные ГОСТом номинальные напряжения для приемников низкого напряжения: Uл = 380 В и Uф = 220 В, Uл = 220 В и Uф = 127 В связаны между собой указанным соотношением.
Четырехпроводная цепь позволяет использовать два напряжения источника питания фазное и линейное. При соединении фаз источника треугольником линейные напряжения равны фазным: Uл = Uф. Как указывалось, на практике фазы обмоток трехфазных генераторов предпочитают соединять звездой прежде всего потому, что в случае отклонения ЭДС источника от синусоидальной формы вследствие наличия высших гармоник сумма мгновенных значений ЭДС не будет равна нулю, и в обмотке источника, соединенной треугольником, при отсутствии нагрузки возникнут токи, которые вызовут ее нагревание и снижение КПД генератора.
2. 4. 4 Трехфазные цепи с симметричными пассивными приемниками
Соединение звездой. Четырехпроводная и трехпроводная цепи
На рис. 2. 18 изображена схема четырехпроводной трехфазной цепи. Если пренебречь сопротивлениями линейных проводов и нейтрального провода, то фазные напряжения приемника и источника будут равны

 ,
,  ,
,  .
.
Тогда токи в каждой фазе приемника определятся по формулам:
 ,
,  ,
, 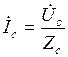 ,
,
ток в нейтральном проводе
İ N = İ a + İ b + İ c.
 Из схемы видно, что при соединении фаз приемника звездой фазные и линейные токи равны между собой, например İ A = İ a. При симметричной нагрузке токи в фазах равны по величине и сдвинуты по фазе на один и тот же угол относительно соответствующих фазных напряжений. Векторная диаграмма напряжений и токов при симметричной нагрузке изображена на рис. 2. 19.
Из схемы видно, что при соединении фаз приемника звездой фазные и линейные токи равны между собой, например İ A = İ a. При симметричной нагрузке токи в фазах равны по величине и сдвинуты по фазе на один и тот же угол относительно соответствующих фазных напряжений. Векторная диаграмма напряжений и токов при симметричной нагрузке изображена на рис. 2. 19.
Из диаграммы следует, что İ A + İ B + İ C = 0, т. е. при симметричной нагрузке ток в нейтральном проводе отсутствует İ N = 0, и необходимость в этом проводе отпадает. Трехфазная цепь без нейтрального провода будет трехпроводной (рис. 2. 20).
 Из схем рис. 2. 18, 2. 20 и векторной диаграммы рис. 2. 19 следует, что при соединении звездой симметричных трехфазных приемников
Из схем рис. 2. 18, 2. 20 и векторной диаграммы рис. 2. 19 следует, что при соединении звездой симметричных трехфазных приемников
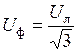 и
и 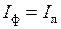 .
.
Для определения токов при симметричной нагрузке достаточно определить ток только в одной из фаз, входящих в трехфазную цепь. В трехпроводную цепь при соединении нагрузки звездой включают только симметричные трехфазные приемники: электрические двигатели, электрические печи и др.
Соединение треугольником
Кроме соединения звездой, широкое применение получили трехпроводные трехфазные цепи с соединением приемников треугольником. Если три фазы приемника с фазными сопротивлениями Zab; Zbc; Zca включены непосредственно между линейными проводами трехпроводной цепи, то получим соединение приемников треугольником (рис. 2. 21).
Из схемы рис. 2. 21 видно, что если пренебречь сопротивлениями линейных проводов, то фазные напряжения приемника будут равны соответствующим линейным напряжениям источника питания: Uф = Uл. В отличие от соединения звездой фазные и линейные токи не равны между собой. Принятым условным положительным направлениям линейных напряжений соответствуют условные положительные направления фазных токов (см. рис. 2. 21). Если сопротивления фаз приемника заданы, то фазные токи определяют по формулам
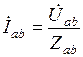 ,
,  ,
, 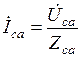 .
.
 Линейные токи определяют по фазным токам из уравнений, составленных согласно первому закону Кирхгофа для узлов a, b, c:
Линейные токи определяют по фазным токам из уравнений, составленных согласно первому закону Кирхгофа для узлов a, b, c:
İ A = İ ab – İ ca, İ B = İ bc – İ ab, İ C = İ ca – İ bc.
Из уравнений следует, что любой из линейных токов равен геометрической разности соответствующих векторов токов тех двух фаз приемника, которые соединяются с данным линейным проводом.
При симметричной нагрузке Zab = Zbc = Zca фазные токи равны по величине и углы сдвига фаз токов по отношению к соответствующим фазным напряжениям одинаковы. Векторная диаграмма напряжений и токов при симметричной нагрузке, соединенной треугольником, изображена на рис. 2. 22. Из диаграммы следует, что соотношение между фазными и линейными токами аналогично соотношению между фазными и линейными напряжениями при соединении нагрузки звездой.
2. 4. 5. Трехфазные цепи с несимметричными пассивными приемниками
Соединение звездой. Четырехпроводная цепь
Благодаря нейтральному проводу (см. рис. 2. 18) напряжения на каждой из фаз приемника при несимметричной нагрузке будут неизменными и равными соответствующим фазным напряжениям источника питания как по величине, так и по фазе, т. е. фазные и линейные напряжения приемника также образуют симметричную систему. Но токи в фазах будут разными. Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Поэтому в четырехпроводную сеть включают однофазные приемники, и режим работы каждого такого приемника, находящегося под неизменным фазным напряжением источника питания, не будет зависеть от режима работы приемников, включенных в другие фазы. Ток в нейтральном проводе зависит не только от характера сопротивлений фаз приемника, но и от схемы их включения.
Если сопротивлением нейтрального провода не пренебрегать (см. рис. 2. 18), то при  фазные напряжения приемника не будут равны соответствующим напряжениям источника. В этом случае между нейтральными точками источника и приемника возникает напряжение
фазные напряжения приемника не будут равны соответствующим напряжениям источника. В этом случае между нейтральными точками источника и приемника возникает напряжение  , называемое напряжением относительно нейтрали или напряжением между нейтралями. Зная
, называемое напряжением относительно нейтрали или напряжением между нейтралями. Зная  , можно определить фазные напряжения приемника.
, можно определить фазные напряжения приемника.
Для определения напряжения относительно нейтрали можно воспользоваться формулой напряжения между двумя узлами, так как схема рис. 2. 18 представляет собой схему с двумя узлами
 ,
,

где  ,
,  ,
,  ,
,  – комплексы проводимостей фаз нагрузки и нейтрального провода. По известным напряжениям
– комплексы проводимостей фаз нагрузки и нейтрального провода. По известным напряжениям 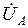 ,
,  ,
,  ,
,  можно построить потенциальную диаграмму (рис. 2. 23) и провести на ней векторы фазных напряжений приемника
можно построить потенциальную диаграмму (рис. 2. 23) и провести на ней векторы фазных напряжений приемника  ,
, 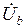 ,
,  . Комплексные значения этих напряжений можно определить, воспользовавшись уравнениями, составленными по второму закону Кирхгофа для схемы рис. 2. 18:
. Комплексные значения этих напряжений можно определить, воспользовавшись уравнениями, составленными по второму закону Кирхгофа для схемы рис. 2. 18:
 ,
,  ,
,  .
.
Зная фазные напряжения приемника, можно определить фазные токи:
 ,
, 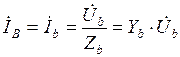 ,
, 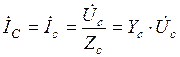 .
.
Ток в нейтральном проводе 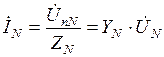 .
.
Правильность расчета можно проверить по формуле
İ N = İ a + İ b + İ c.
При увеличении сопротивления нейтрального провода эффективность его использования уменьшается: чем больше величина  , тем больше фазные напряжения приемника отличаются от фазных напряжений источника. В случае обрыва нейтрального провода (YN = 0, ZN = ∞ ) при несимметричной нагрузке величина
, тем больше фазные напряжения приемника отличаются от фазных напряжений источника. В случае обрыва нейтрального провода (YN = 0, ZN = ∞ ) при несимметричной нагрузке величина  будет максимальной. По этой причине плавкий предохранитель в нейтральный провод не ставят: при перегорании предохранителя на фазах нагрузки могут возникнуть значительные перенапряжения. В нейтральный провод также не вводят выключатель.
будет максимальной. По этой причине плавкий предохранитель в нейтральный провод не ставят: при перегорании предохранителя на фазах нагрузки могут возникнуть значительные перенапряжения. В нейтральный провод также не вводят выключатель.
Соединение треугольником. Трехпроводная цепь
При несимметричной нагрузке (см. р
|
|
|


