Главная | Обратная связь | Поможем написать вашу работу!

1.6. Передача энергии от активного двухполюсника нагрузке

Если нагрузка R подключена к активному двухполюснику (рис. 1. 10), то через нее пойдет ток , и в ней будет выделяться мощность

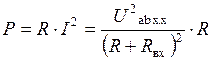. (1. 19)

Выясним, каково должно быть соотношение между сопротивлением нагрузки и входным сопротивлением двухполюсника R_вх, чтобы в сопротивлении нагрузки выделялась максимальная мощность; чему будет она равна и каков при этом будет КПД передачи. С этой целью найдем первую производную P по R и приравняем ее нулю (исследуем функцию на экстремум):

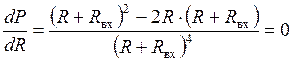Отсюда R = R_вх. (1. 20)

Нетрудно найти вторую производную и убедиться в том, что она отрицательна 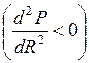, поэтому соотношение (1. 20) соответствует максимуму функции P = f (R).

Подставим (1. 20) в (1. 19) и найдем максимальную мощность, которая может быть выделена в нагрузке R:

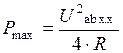. (1. 21)

Полезная мощность, выделяющаяся в нагрузке, определяется уравнением (1. 19). Полезная мощность, выделяемая эквивалентным генератором,

. (1. 22)

Коэффициент полезного действия

. (1. 23)

Если R = R_вх, то η = 0, 5.

Если мощность P значительна, то работать с таким низким КПД, как 0, 5, совершенно недопустимо. Но если мощность P мала, например, составляет всего несколько милливатт (такой мощностью обладают, например, различные датчики устройств автоматики), то с низким КПД можно и не считаться, поскольку в этом режиме датчик отдает нагрузке максимально возможную мощность. Выбор величины сопротивления нагрузки R, равного входному сопротивлению R_вх активного двухполюсника, называют согласованием нагрузки.

2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

2. 1. Основные величины, характеризующие синусоидальные величины функции времени

Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону:

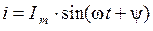где i – мгновенное (зависящее от времени) значение тока; I_m – амплитуда тока; ω t + ψ – фазовый угол или фаза синусоидально изменяющейся величины, t – текущее значение времени, ψ – начальная фаза тока, равная значению фазового угла в момент времени t = 0, в радианах или градусах,

– угловая скорость (угловая частота) переменного тока, представляющая собой скорость изменения фазового угла.

График его дан на рис. 2. 1. Время, в течение которого совершается полный цикл изменения синусоидальной величины, называется периодом колебаний и обозначается Т. Величина 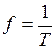(Гц) называется частотой переменного тока и равна числу полных циклов изменения синусоидальной величины за 1 секунду. За время одного периода фазовый угол синусоидальной величины изменяется на 2π радиан или . Поэтому угловая скорость (частота) (рад/с). На электрической схеме стрелкой указывается условное положительное направление синусоидальной величины.

Начальная фаза ψ, представляющая собой алгебраическую величину, положительна, когда гармоническая функция смещена влево относительно начала координат, отрицательна когда функция смещена вправо. Если сдвиг фаз между двумя гармоническими колебаниями x₁(t) и x₂(t) положителен ( 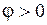), то говорят, что колебание x₁(t) опережает колебание x₂(t). При говорят, что колебания x₁(t) и x₂(t) находятся в фазе. При сдвиге фаз говорят, что колебания находятся в противофазе, а при 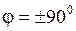– в квадратуре.

Любое гармоническое колебание с произвольной начальной фазой можно представить в виде суммы двух колебаний с нулевыми начальными фазами, находящихся в квадратуре:

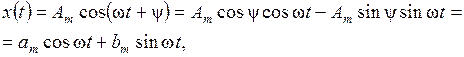
где , ,

, .

Линейная комбинация нескольких гармонических колебаний с одной и той же частотой дает результирующее гармоническое колебание той же частоты. Дифференцирование и интегрирование гармонических колебаний приводит к гармоническим колебаниям той же частоты, сдвинутыми по фазе на :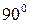

При совместном рассмотрении двух синусоидально изменяющихся величин одной частоты разность их фазовых углов называют углом сдвига фаз. Угол сдвига фаз между синусоидами напряжения 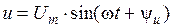и тока элемента цепи обозначают буквой .

При анализе электрических цепей чаще оперируют среднеквадратичным (действующим) значением электрических величин, в которых градуируются электроизмерительные приборы. Действующее значение синусоидального тока связано с амплитудным значением тока следующим соотношением

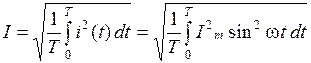Так как

то среднеквадратичное значение синусоидального тока меньше его амплитуды в раз:

Под средним значением синусоидального тока понимают их среднее максимальное значение за период. Если ток 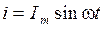, то его среднее значение

2. 2. Представление синусоидальных функций в различных формах

Синусоидальная функция времени i(t) может быть получена как проекция на вертикальную (мнимую) ось комплексной плоскости вектора I_m (рис. 2. 2), вращающегося в положительном направлении (против часовой стрелки) с угловой частотой ω.

Поскольку при расчете сложных цепей операции с гармоническими трансцендентными функциями затруднительны, на практике применяют комплексные представления гармонических колебаний. В электротехнике нашел применение символический метод расчета электрических цепей. Каждой синусоидальной величине на комплексной плоскости ставится в соответствие вектор.

Вектору на комплексной плоскости соответствует определенное комплексное число (символ)

называемое комплексной амплитудой тока. Мнимая единица .

Положение вектора на комплексной плоскости однозначно задано, если известны его длина (модуль) и угол 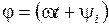, под которым он проведен, – это показательная форма записи комплексного чи сла. Положение вектора на комплексной плоскости однозначно задано, если известны две его проекции на координатные оси. Это алгебраическая форма записи I_m комплексного числа . Переход от показательной формы записи к алгебраической форме записи производят с помощью тригонометрических преобразований

Переход от алгебраической формы записи к показательной форме производят с помощью тех же тригонометрических преобразований:

, .

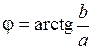Большой буквой с точкой наверху обозначают только комплексные изображения синусоидальных функций времени. Математическое описание синусоидальной функции дано на примере тока i(t). Аналогично описывают математически ЭДС e(t), напряжение u(t) и потокосцепление ψ (t).

Используя показательную и алгебраическую формы комплексной величины (воздействия) x(t) = A_mej(ω t + ψ ), аргумент которой растет пропорционально времени t, легко показать, что гармонические функции представляют собой проекции этого вращающегося вектора наоси мнимых и вещественных чисел комплексной плоскости.

Действительно,

где – комплексная амплитуда гармонического воздействия.

Таким образом, синусоидальная функция времени представляет собой проекцию вращающегося с угловой скоростью ω вектора A_m, длина которого равна амплитуде колебаний A_m, на ось мнимых чисел, а косинусоидальная функция времени – проекцию вращающегося вектора A_m на ось вещественных чисел комплексной плоскости:

; .

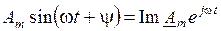Если расчет процессов в электрической цепи при гармонических воздействиях одинаковой частоты ω выполнять на комплексной плоскости, то все воздействия и реакции будут изображаться вращающимися с одинаковой скоростью ω векторами, неподвижными друг относительно друга. Это обстоятельство позволяет изображать гармонические функции A_m = A_me ^j^φ комплексными числами, которые характеризуются только амплитудой A_m и начальной фазой ψ. При этом линейные операции над мнимыми и вещественными частями комплексных чисел заменяются операциями над самими комплексными числами. Это возможно благодаря коммутативности линейных операций относительно выделения вещественной и мнимой частей.

Комплексные воздействия обладают рядом важных для анализа электрических цепей свойств. Любое комплексное воздействие можно представить в виде суммы двух квадратурных колебаний:

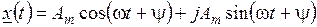Дифференцирование комплексного воздействиясво д ится к умножению его комплексной амплитуды на оператор поворота ,

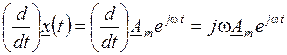Интегрирование комплексного воздействия сводится к делению его комплексной амплитуды на ,

Использование комплексных изображений значительно упрощает расчет цепей. Дело в том, что интегро-дифференциальные уравнения цепи при расчете методом комплексных амплитуд сводятся к алгебраическим уравнениям относительно комплексных амплитуд воздействия и реакции, а общий множитель e ^{jω t}, который входит в выражения x(t) и y(t), сокращается.

Пример 2. 1. Дано гармоническое колебание . Определить амплитуды квадратурных составляющих колебаний, представить данное колебание в комплексной форме.

Решение. Амплитуды квадратурных колебаний

, .

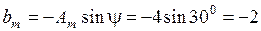Комплексная амплитуда колебания имеет вид

а изображение его на комплексной плоскости

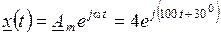2. 3. Основные элементы и параметры электрической цепи синусоидального тока

Пассивными линейными элементами (приемниками) электрической цепи синусоидального тока являются:

резистивный элемент (резистор), обладающий сопротивлением R;

индуктивный элемент (индуктивная катушка) с индуктивностью L;

емкостной элемент (конденсатор) с емкостью C.

Сопротивление, индуктивность и емкость являются коэффициентами пропорциональности в выражениях для напряжения u, потокосцепления 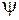и количества электричества q в линейных цепях через ток и напряжение:

u = R∙ i; ψ = L∙ i; q = C∙ i.

Индуктивный элемент рассматривают как зависимый источник напряжения, ЭДС которого по закону электромагнитной индукции , если он рассматривается как источник и положительное направление для ЭДС и тока принимают совпадающими, или 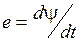, если он рассматривается как приемник и положительное направление ЭДС принимается противоположным условно-положительному направлению, выбранному для тока. В обоих случаях напряжение на зажимах индуктивного элемента

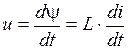2. 3. 1. Электрическая цепь с резистивным элементом

Предположим, что через резистивный элемент с сопротивлением R подано синусоидальное напряжение . Необходимо установить, как будут изменяться ток и мощность этой цепи. Ток в цепи можно определить, пользуясь законом Ома для мгновенных значений:

или

, .

Синусоида тока имеет ту же частоту, что и синусоида напряжения и совпадает с ней по фазе.

Амплитуда тока связана с амплитудой напряжения соотношением

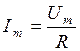Поделив обе части уравнения на , получим соотношение для действующих значений тока и напряжения

Мгновенное значение мощности этой цепи равно произведению мгновенных значений напряжения и тока:

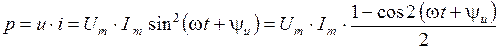
или

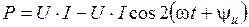Среднее за период значение мощности

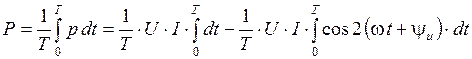или

P = U ∙ I.

Если в выражение для средней мощности вместо напряжения подставить его значение U = R ∙ I, то получим, что среднее значение мощности в цепи равно ее активной мощности:

P = U ∙ I = R ∙ I².

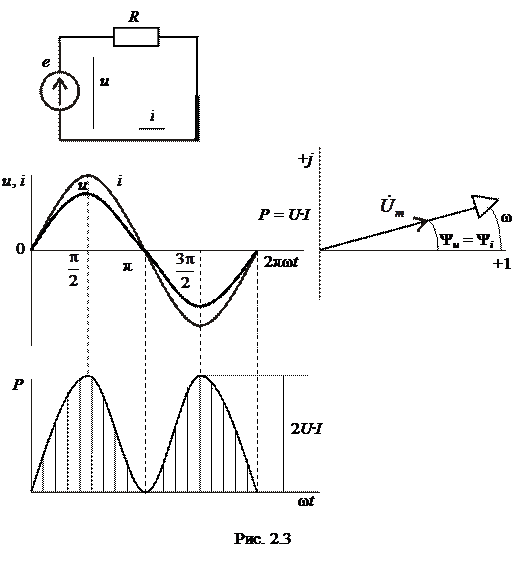
Для иллюстрации изменений напряжения, тока и мощности в резисторе на рис. 2. 3 построены графики для случая, когда начальная фаза ψ _u = 0. Для построения векторной диаграммы напряжения и тока цепи на комплексной плоскости запишем их комплексные амплитуды:

, .

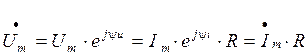Вектор, изображающий синусоиду напряжения на резисторе, совпадает по направлению с вектором, изображающим синусоиду тока.

При расчете цепей синусоидального тока вместо векторов комплексных амплитуд принято строить векторы комплексных действующих значений напряжения и тока İ . Эти векторы совпадают по направлению с векторами İ _m и 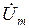и отличаются от них только по величине:

Из последнего уравнения можно получить закон Ома в комплексной форме для цепи с резистивным элементом

2. 3. 2. Электрическая цепь с идеальной индуктивной катушкой

Предположим, что в катушке с индуктивностью L, активное сопротивление которой равно нулю, имеется синусоидальный ток (рис. 2. 4)

Этот ток создает в катушке синусоидально изменяющийся поток

амплитуда потока

а начальная фаза и частота равны начальной фазе и частоте тока. Синусоидально изменяющийся поток катушки наводит в ней ЭДС самоиндукции

Синусоида ЭДС самоиндукции отстает по фазе от синусоиды тока на угол сдвига фаз . Амплитуда синусоиды ЭДС U_Lm = ω LI_m, а ее среднеквадратичное значение E_L = ω LI. Внешнее напряжение источника u = u_L уравновешивается ЭДС самоиндукции e_L. Синусоида этого напряжения

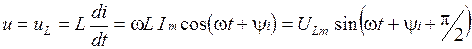Синусоида индуктивного напряжения идеальной катушки опережает по фазе ток на угол сдвига фаз . Амплитуда синусоиды напряжения на катушке U_Lm = ω LI_m, среднеквадратичное значение этого напряжения U_L = ω LI.

Комплексные амплитуды тока и напряжения:

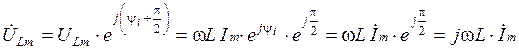Вектор напряжения на идеальной катушке опережает по фазе вектор тока на угол сдвига фаз . На рис. 2. 4 приведены графики синусоид напряжения u_L, тока i, ЭДС самоиндукции e_L и соответствующие этим синусоидам векторы их комплексных значений для случая ψ _i = 0. Произведение 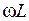имеет размерность сопротивления, его обозначают x_L и называют индуктивным сопротивлением катушки:

x_L = ω L = 2π fL.

Величину jω L = jx_L называют комплексом индуктивного сопротивления.

Закон Ома в комплексной форме для идеальной индуктивной катушке имеет вид

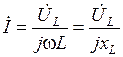Мгновенное значение мощности в цепи с идеальной катушкой индуктивности

График этой мощности для случая ψ _i = 0 приведена на рис. 2. 4. В первую четверть периода, когда ток и напряжение положительны, мощность также положительна. Энергия 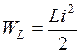от источника переходит в цепь и затрачивается на создание магнитного поля. К концу первой четверти периода поле имеет максимальную энергию , пропорциональную заштрихованной площади, ограниченной осью абсцисс и первой полуволной синусоиды мощности. Во вторую четверть периода ток i убывает, но остается положительным. Напряжение u_L и мощность p_L отрицательны. Энергия магнитного поля возвращается обратно в источник. К концу второй четверти периода весь запас энергии будет возвращен источнику. Поэтому среднее за период значение мощности цепи с идеальной катушкой равно нулю:

Таким образом, в цепи с идеальной катушкой индуктивности происходит непрерывное колебание (обмен) энергии между источником и магнитным полем катушки без затраты энергии источника.

Амплитуду колебаний мощности в цепи с идеальной катушкой называют реактивной индуктивной мощностью и обозначают Q_L:

Q_L = U_LI = x_LI².

Реактивная мощность имеет ту же размерность, что и активная мощность. Но с целью удобства для единиц измерения реактивной мощности принято другое наименование: вольт-ампер реактивный (ВАр).

2. 3. 3. Электрическая цепь с идеальным конденсатором

Пусть к конденсатору (рис. 2. 5) подведено синусоидальное напряжение

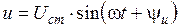Ток в конденсаторе

Амплитуда тока I_m = ω ∙ C∙ U_cm. Среднеквадратичное значение тока

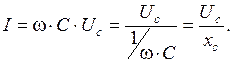Величину

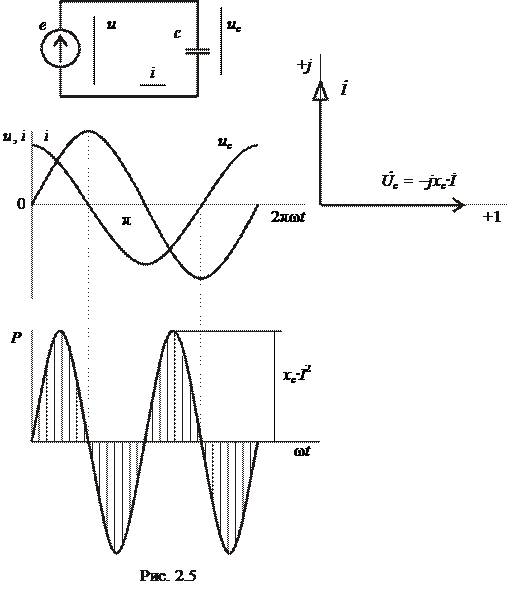имеющую размерность сопротивления, называют емкостным сопротивлением. Емкостное сопротивление обратно пропорционально частоте источника питания и емкости конденсатора.

Синусоида емкостного тока опережает по фазе синусоиду напряжения на конденсаторе на угол сдвига фаз . На рис. 2. 5 построены графики i, u_c, векторы среднеквадратичных значений тока и напряжения на конденсаторе для случая, когда начальная фаза ψ _u = 0.

Комплексные амплитуды напряжения и тока равны:

Разделив правую и левую части последнего выражения на , получим уравнение, связывающее комплексные значения тока и напряжения:

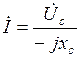где (– jx_c) – комплекс емкостного сопротивления.

Это уравнение выражает закон Ома в комплексной форме для участка цепи с идеальным конденсатором. Комплекс тока конденсатора равен комплексу напряжения, деленному на комплекс емкостного сопротивления конденсатора.

Мгновенное значение мощности

Среднее за период значение мощности цепи с идеальным конденсатором равно нулю:

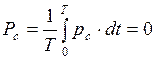Как и в цепи с идеальной катушкой, здесь наблюдаются процессы колебания энергии – чередование промежутков времени, в течение которых энергия от источника запасается в электрическом поле конденсатора, с промежутками времени, когда энергия возвращается обратно источнику.

Амплитуду колебаний мощности в цепи с конденсатором называют реактивной емкостной мощностью и обозначают Q_c = U_cI = x_cI².

Как и реактивная индуктивная мощность, реактивная емкостная мощность измеряется в ВАр.

2. 3. 4. Электрическая цепь с реальной индуктивной катушкой

Пусть в реальной индуктивной катушке с индуктивностью L и активным сопротивлением R имеется ток Необходимо установить закон изменения напряжения u на ее зажимах.

Заменим реальную катушку пассивным двухполюсником, состоящим из последовательно соединенного резистивного элемента с сопротивлением R и индуктивного элемента с индуктивностью L. Согласно второму закону Кирхгофа мгновенное значение напряжения двухполюсника

где u_R и u_L – соответственно напряжения на резистивном и индуктивном элементах катушки.

Амплитуду U_m и начальную фазу ψ _n напряжения u определим, пользуясь комплексным методом. С этой целью от уравнения электрического состояния для мгновенных значений перейдем к уравнениям для комплексных значений напряжений и тока:

Комплексное значение тока 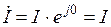, комплексные значения напряжений , 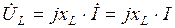. Тогда комплексное напряжение на входе цепи

Комплексная величина Z = R + jx_L называется комплексом полного сопротивления индуктивной катушки. В формулах пользуются и показательной формой записи комплекса полного сопротивления

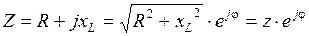где – модуль комплекса полного сопротивления,

– его аргумент.

Комплекс напряжения можно записать в следующем виде

Закон Ома для рассматриваемой цепи в комплексной форме:

На рис. 2. 6 приведена векторная диаграмма цепи. При построении этой диаграммы за исходный взят вектор тока İ , совпадающий с осью +1. Вектор напряжения на резисторе совпадает по фазе с вектором тока. Вектор напряжения на индуктивном элементе опережает по фазе вектор тока на угол сдвига фаз . Вектор напряжения равен геометрической сумме векторов , он опережает вектор тока на угол сдвига фаз .

Векторную диаграмму на рис. 2. 6 называют треугольником напряжений. Если каждую из сторон треугольника напряжений разделить на İ , то получим треугольник комплексов сопротивлений.

2. 3. 5. Мощность индуктивной катушки

Пусть ток в индуктивной катушке изменяется по закону , напряжение на индуктивной катушке . Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:

Среднее за период значение мощности

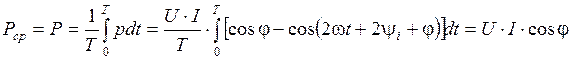Так как U = z ∙ I, а , то среднее значение мощности можно определить иначе: .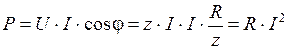

Из полученного соотношения видно, что среднее значение мощности цепи равно ее активной мощности. Поэтому среднюю мощность цепи синусоидального тока обычно называют активной мощностью. Активная мощность равна произведению действующих значений напряжения и тока на косинус угла сдвига фаз между ними.

Наибольшее значение активной мощности, которое быть получено при данных значениях напряжения тока, называют полной мощностью и обозначают S.

Величина является реактивной индуктивной мощностью цепи.

Активная, реактивная и полная мощности находятся в квадратуре:

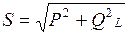Хотя все три мощности цепи (активная, реактивная и полная) имеют одну и ту же размерность, для их различия введены единицы различных наименований: для активной мощности ватты (Вт, кВт, МВт), для реактивной мощности – вольт-амперы реактивные (ВАр, кВАр, МВАр), для полной мощности – вольт-амперы (ВА, кВА, МВА).

Полная мощность является расчетной мощностью машины, так как эта мощность учитывает напряжение и ток, по величинам которых выбирают все элементы электротехнических устройств и аппаратов. Поэтому в паспорте машин указывается их полная мощность.

Активная мощность Р является средней мощностью преобразования электрической энергии в другие виды. Величина Р зависит не только от тока и напряжения, но также от 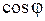, который обычно называют коэффициентом мощности:

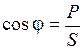Коэффициент мощности зависит от соотношения между активным и индуктивным сопротивлениями. По его величине судят о том, какую часть полной мощности цепи составляет активная мощность.

Реактивная мощность Q_L характеризует амплитуду колебания мощности обмена энергией между источником и магнитным полем катушки.

Активную, реактивную и полную мощности можно получить по комплексным значениям напряжения 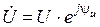и тока . Для этого необходимо взять сопряженный комплекс тока (обозначается звездочкой) 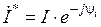и умножить его на комплекс напряжения :

Это произведение обозначают буквой 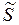и называют комплексом полной мощности

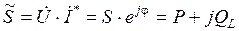2. 3. 6. Последовательное соединение резистора и конденсатора

Предположим, что в двухполюснике (рис. 2. 7), состоящем из последовательно соединенных резистора и идеального конденсатора, имеется синусоидальный ток .

Напряжение на входе этого двухполюсника согласно второму закону Кирхгофа в комплексной форме

Комплексное значение тока может быть записано по заданному уравнению мгновенного значения тока:

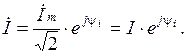
Тогда комплексы активного и емкостного напряжений 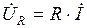, 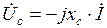. Комплекс напряжения на входе двухполюсника

Из этого уравнения можно получить формулу закона Ома в комплексной форме

Комплекс полного сопротивления емкостного двухполюсника

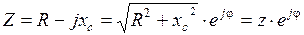где – модуль комплекса полного сопротивления цепи, а

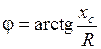– его аргумент.

На рис. 2. 7 построен треугольник напряжений для заданного двухполюсника. Для упрощения построения начальная фаза тока ψ _i принята равной нулю. Вектор тока İ направлен по оси + 1. С ним совпадает по фазе вектор активного напряжения и отстает от него по фазе на угол сдвига фаз вектор напряжения на конденсаторе . Результирующий вектор напряжения на входе двухполюсника отстает по фазе от вектора тока на угол сдвига фаз .

Мгновенная мощность емкостного двухполюсника

Среднее за период значение мощности

Как и для индуктивного двухполюсника, среднее значение мощности емкостного двухполюсника равно его активной мощности, так как

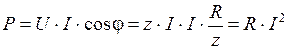Реактивная мощность, характеризующая амплитуду мощностиобмена энергией между цепью и электрическим полем конденсатора,

Полная мощность

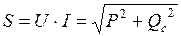Комплекс полной мощности

Согласно уравнению комплекс реактивной мощности является отрицательной мнимой частью полной мощности.

2. 3. 7. Последовательное соединение резистора, индуктивной катушки и

конденсатора

Обычно индуктивная катушка и конденсатор имеют потери, поэтому схема замещения последовательно соединенных катушки и конденсатора состоит из двухполюсника с последовательным соединением элементов R, L и С, как показано на рис. 2. 8. Если по этому двухполюснику пропустить ток 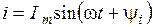, комплексное значение которого , то согласно второму закону Кирхгофа в комплексной форме для напряжения на входе двухполюсника можно записать уравнение

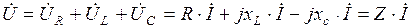Величина Z = R + jx_L – jx_C представляет собой комплекс полного сопротивления двухполюсника. В зависимостиот соотношения между индуктивным и емкостным сопротивлениями двухполюсника последний может

быть: 1) индуктивным (x_L > x_C), 2) емкостным (x_L < x_C) и 3) чисто активным (x_L = x_C). Комплексы полных сопротивлений двухполюсника в этих случаях определяются следующими уравнениями:

1) Z = R + j(x_L– x_C),

2) Z = R – j(x_L– x_C),

3) Z = R.

На рис. 2. 8 построены векторные диаграммы для указанных трех случаев. Начальная фаза тока ψ _i на этих диаграммах принята равной нулю. Для упрощения записи комплексов полных сопротивлений двухполюсников с индуктивными и емкостными элементами вводят понятие реактивного сопротивления двухполюсника, которое обозначают буквой x. Оно является алгебраической суммой индуктивного и емкостного сопротивлений: x = x_L – x_C. При x > 0 двухполюсник будет индуктивным, при x < 0 – емкостным и при x = 0 – чисто активным. Тогда комплекс полного сопротивления двухполюсника для всех трех случаев записывается в виде Z = R + jx. Модульполного сопротивления двухполюсника .

Аргумент или угол сдвига фаз между векторами напряжения и тока двухполюсника